期末复习（一）曲线运动、万有引力部分
知识点复习：
（一）曲线运动
1. 曲线运动
（1）曲线运动定义：轨迹是曲线的运动。
（2）曲线运动的速度方向和性质：
速度方向就是该点的切线方向，曲线运动的速度方向时刻改变，故曲线运动一定存在加速度，曲线运动一定是变速运动。
（3）物体做直线运动条件：物体所受合外力为零或所受合外力方向和物体运动方向在同一直线上。
（4）物体作曲线运动条件：合外力方向与速度方向不在同一直线上。
2. 运动的合成和分解
（1）有关运动的合成和分解的几个概念：
如果某物体同时参与几个运动，那么这物体实际运动就叫做那几个运动的合运动，那几个运动叫做这个实际运动的分运动。已知分运动情况求合运动情况叫运动的合成，已知合运动情况求分运动情况叫运动的分解。
合运动的位移叫做合位移；分运动的位移叫分位移。合运动在一段时间内的平均速度叫合速度；分运动在该同一段时间内的平均速度叫分速度。
（2）运动的合成及分解规则：平行四边形定则。
① 合运动一定是物体的实际运动。
② 分运动之间是相互不相干的。
③ 合运动和各分运动具有等时性。
④ 合运动和分运动的位移、速度、加速度都遵守平行四边形定则。
⑤ 特例：
<1> 初速为
的匀加速直线运动，可看成是同方向的一个匀速运动和另一个初速为零的匀加速直线运动的合运动。
<2> 竖直上抛运动可看成是一个竖直向上的匀速直线运动和另一个自由落体运动的合运动。
<3> 两个匀速直线运动合成后一定是匀速直线运动。
<4> 不在同一直线上的一个匀速直线运动和一个变速直线运动合成后运动轨迹是曲线（合运动的加速度方向和合运动速度方向不在同一直线上）。
3. 平抛运动
（1）平抛运动的定义：水平抛出物体只在重力作用下的运动。
（2）平抛运动性质：是加速度恒为重力加速度g的匀变速曲线运动，轨迹是抛物线。
（3）平抛运动的处理方法：
分解为
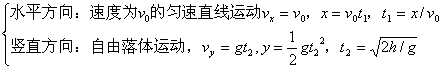
结果得
注意：运动学公式只适用于直线运动，因此曲线运动要分解成两个直线的分运动后才能应用运动学公式求解。
4. 匀速圆周运动
（1）匀速圆周运动的定义：相等的时间内通过的圆弧长度都相等的圆周运动。
（2）描述圆周运动快慢的几个物理量：
① 线速度v：大小为通过的弧长跟所用时间的比值，方向为圆弧该点切线方向；
；
②
角速度
：大小为半径转过的角度跟所用时间的比值，方向可用右手螺旋定则判定（高中阶段不研究）；
；
③ 周期T：沿圆周运动一周所用的时间；
④ 频率f：每秒钟完成圆周运动的转数。
（3）线速度、角速度、圆期、频率之间的关系：
（4）
注意：①
、T、
三个量中任一个确定其余两个也就确定，但v还和r有关；② 固定在同一根转轴上转动的物体其角速度相等；③
用皮带传动的皮带轮轮缘（皮带触点）线速度大小相等。
（5）做匀速圆周运动的物体所受的合外力：总是指向圆心，作用效果只是使物体速度方向发生变化。
（6）向心力定义：使物体速度方向发生变化的合外力。
注意：① 向心力方向总是指向圆心，时刻在变化，是一个变力；② 向心力是根据力的作用效果命名的，它可以是重力、弹力、摩擦力等各种性质的力，也可以是它们的合力，还可以是某个力的分力；③ 向心力只改变速度方向，不改变速度的大小。
（7）向心力大小（实验演示）：跟物体质量m、圆周半径r和运动的角速度有关，其关系为：
（高中阶段不要求推导）。
（8）向心加速度：
① 概念：向心力产生的加速度，只是描述线速度方向变化的快慢。
② 大小：
。
③ 方向：总是指向圆心，时刻在变化，是一个变加速度。
④ 注意：当为常数时，
与r成正比；当v为常数时，与r成反比；若无特殊条件，不能说与r成正比还是反比。
（9）匀速圆周运动的性质：加速度大小不变，方向时刻改变，所以是非匀变速曲线运动。
注意：
① 匀速圆周运动只是线速度方向改变而速率不变，所以其所受合外力全部用来改变速度方向，即合外力等于向心力，由于速率不变，向心加速度和向心力大小不变；② 变速圆周运动，线速度大小、方向都改变，所以合外力不等于向心力，向心力只是等于合外力沿着圆周法线方向的分力，且向心加速度和向心力的大小、方向都不断改变。
（10）火车转弯情况：外轨略高于内轨，使得火车所受重力和支持力的合力
提供向心力。
（由
得
）。（R、h、L各分别为转弯处轨道半径，内外轨高度差，两轨道间距离）
① 当火车行驶速率v等于时，
，内、外轨道对轮缘都没有侧压力；
② 当火车行驶速度v大于时，
，外轨道对轮缘有侧压力；
③ 当火车行驶速度v小于时，
，内轨道对轮缘有侧压力。
（11）汽车过拱桥情况：① 汽车通过凸形桥最高点时汽车对桥面的压力小于汽车重力② 汽车通过凹形桥最低点时汽车对桥面的压力大于汽车重力
5. 离心现象：
（1）离心运动的定义
做匀速圆周运动的物体，在合外力突然消失或者不足以提供它做圆周运动所需的向心力时，做逐渐远离圆心的运动，这种运动叫离心运动。
（2）离心运动的应用和危害
利用离心运动制成离心机械。例如离心干燥器、洗衣机的脱水筒等等。
汽车、火车转弯处，为防止离心运动造成的危害，一是限定汽车和火车转弯速度不能太大；二是把路面筑成外高内低的斜坡以增大向心力。
（二）万有引力定律
1. 行星运动的三大规律
（1）所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个焦点上。
（2）对每一个行星而言，太阳行星的连线在相同时间内扫过的面积相等。
（3）所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。其表达式为：
，其中R是椭圆的轨道的半长轴，T是行星绕太阳公转的周期，k是一个与行星无关的常量。
2. 万有引力定律：
（1）内容：自然界中任何两个物体都是互相吸引的。两个物体间的引力大小，跟它们的质量的乘积成正比，跟它们的距离的平方成反比。
（2）公式：
。其中
，称为万有引力恒量。
（3）注意：严格来说公式只适用于质点间的相互作用，当两物体的距离远大于物体本身大小时，公式也近似适用，但此时它们间距离r应为两物体质心间距离。
3. 引力常量的测定：卡文迪许扭秤实验。
4. 物体的重力随离地面高度h的变化情况：物体的重力近似为地球对物体的引力。即近似等于G
，可见物体重力随h的增大而减少。
5. 重力加速度g随离地面高度h的变化情况：
，可见g随h增大而减少。
6. 万有引力定律在天文学上的应用
（1）求天体质量M、密度
的方法；
通过观测天体卫星运动的周期T、轨道半径r，把卫星的运动看成匀速圆周运动，根据向心力来源于万有引力得：
。 ∴ 
。
如果知天体的半径R可得天体的体积为
。
∴
（如果卫星在天体表面运行，
，
）。
（2）研究天体运动情况的一般方法：把天体运动看成匀速圆周运动，向心力来源于万有引力，即：
。
根据研究的实际情况选用恰当的公式进行分析，必要时还可用到物体在天体表面时受到的引力等物体的重力。
即：
。
（3）海王星及冥王星的发现
7. 人造卫星、宇宙速度
（1）第一宇宙速度（环绕速度）：
。是地球卫星的最小发射速度。
推导①：当卫星在地球附近运行时，
，
由
得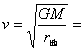
推导②：当卫星在地球附近运行时，
，。
由
得
。
（2）第二宇宙速度（脱离速度）：
，使物体可以挣脱地球吸引力束缚，成为绕太阳运行的人造行星（或飞到其他行星上去）的最小发射速度。
（3）第三宇宙速度（逃逸速度）：16.7km/s，使物体挣脱太阳引力的束缚，飞到太阳系以外的宇宙空间去的最小发射速度。
（4）卫星绕行速度、角速度、周期与半径的关系：
① 由
得：
即
；（r越大v越小）
可见第一宇宙速度也可以说成是卫星环绕地球的最大速度。
② 由
得：
即
；（r越大越小）
③ 由得：
即
。（r越大T越大）
（5）地球同步卫星：运转周期与地球自转周期相同（T=24h），所有的地球同步卫星的轨道平面均在赤道平面内，且轨道半径和环绕速度均相同。
推导：由得：
。
∵ T恒定，∴ r恒定。
【典型例题分析】
[例1] 如图1所示，在倾角
的斜面底端的正上方H处，平抛一个物体，该物体落到斜面上的速度方向正好与斜面垂直，则物体抛出时的初速度为：
A. 
B. 
C. 
D. 
分析与解答：如图2所示，分解平抛物体的位移和末速度。设水平分位移为
，末速度的竖直分速度为
，由题意知，
夹角与斜面倾角
相等，利用三角函数关系可以得到：
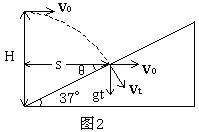
（1）
由平抛运动规律有：
（2）
（3）
由上面三式得到：
（4）
从图中可以看出：
（5）
将（1）（4）两式代入（5）式有：
故
，选项
正确。
注意：解本题的关键之一在于利用矢量分解的知识将末速度和位移正交分解，建立起各物体量之间的几何关系：如与，
与
之间的关系；关键之二是根据平抛规律将水平位移与竖直位移，水平速度与竖直速度通过时间联系在一起，从而建立运动学关系，最后将两种关系结合起来便可解决这一类平抛问题。
[例2] 用细绳栓着质量为
的物体，在竖直平面内作圆周运动，则下列说法正确的是（如图3所示）：（ ）
A. 小球过最高点时，绳子张力可以为零
B. 小球过最高点时的最小速度是0
C. 小球刚好过最高点时的速度是
D. 小球过最高点时，绳子对小球的作用力可以与球所受重力方向相反
分析和解答：小球在最高点时，受重力、绳子拉力（竖直向下，注意绳子不能产生竖直向上的支持力。）所以
，可见，越大时，
越大，越小时，越小，当
时，
得
。故
正确，请注意“刚好通过”的意思可以由以下分析过程而得出：①
很大时，可保证小球通过最高点，但很大。② 很小
时，由于
，而重力一定，重力大于小球所需向心力，小球向圆心偏，不能达到最高点，此时。③ 
时，
，即刚好通过。
[例3] 上例中，把绳子换成细杆时，又是哪个答案正确？（图4所示）
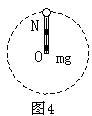
分析与解答：小球在最高点受重力
，杆对球作用力
，取指向圆心方向为正向，故
，所以
，可见：① 当很大时，
，即杆对球产生拉力；② 当很小时，为负值，即杆对球产生支持力，当为零时，
，小球刚好通过最高点；③ 时，
，故正确答案是
【模拟试题】
（答题时间：90分钟）
一. 选择题：本大题共12小题，每小题3分，共36分。每题至少有一个选项是正确的，全部选对的3分，选对但不全得2分，选错或没选得0分。
1. 静止在水平地面上的物体，在恒力F的作用下发生位移s，在地面光滑和不光滑两种情况中（ ）
A. 无摩擦时，力F对物体做的功多 B. 有摩擦时，力F对物体做的功多
C. 无摩擦时，物体获得的动能大 D. 不论有无摩擦物体获得的动能一样大
2. 一质量为m的木块静止在光滑的水平地面上，用大小为F方向与水平成角的恒力作用在该木块上，经过时间t，力F的即时功率为（ ）
A. 
B.
C. 
D.
3. 一个水平力F作用在物体上，使它在力的方向上移动了一段距离S，力F做的功为
，功率为
；若减小物体与水平面间的摩擦力，仍用水平力作用于该物体，使它在力的方向上移动同样的距离S，做的功为
，功率为
，则以下结论正确的是（ ）
A. 
，
B.
，
C. 
， D.
，
4. 如图1所示，用同种材料制成一个轨道ABC，AB段为1/4圆弧，半径为R，水平放置的BC段长为R，一小物块质量为m，与轨道间摩擦因数为
，当它从轨道顶点A由静止开始下滑时，恰好运动到C停止，那么物块在AB段克服摩擦力所做的功为（ ）
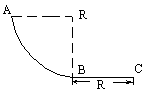
图1
A. 
B. 
C. 
D. 
5. 如图2所示，质量为m的物体以速度v离开高H的桌子，它经A点时，如不计阻力（取地面为零势面），则其具有的机械能是（ ）
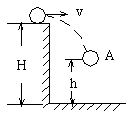
图2
A. 
B.
C. 
D.
6. 做匀速圆周运动的物体（ ）
A. 速度不变 B. 加速度不变 C. 角速度不变 D. 速率不变
7. 下列关于曲线运动的描述中，正确的是（ ）
A. 曲线运动可以是匀速率运动 B. 曲线运动一定是变速运动
C. 曲线运动可以是匀变速运动 D. 曲线运动的加速度可能为零
8. 关于平抛运动，下列说法正确的是（ ）
A. 平抛运动是匀变速运动
B. 平抛运动是非匀变速运动
C. 可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动
D. 落地时间和落地时的速度只与抛出点的高度有关
9. 水平匀速转动的圆盘上的物体相对于盘静止，则圆盘对物体的摩擦力的方向是（ ）
A. 沿圆盘平面指向转轴 B. 沿圆盘平面背离转轴
C. 沿物体做圆周运动轨迹的切线方向 D. 无法确定
10. 如图3所示，P、Q两点在同一竖直平面内，且P点比Q点高，从P、Q两点同时相向水平抛出两个物体，不计空气阻力，则（ ）
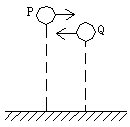
图3
A. 一定会在空中某点相遇 B. 根本不可能在空中相遇
C. 有可能在空中相遇 D. 无法确定能否在空中相遇
11. 如图4所示，质量为m的木块，从半径为r的竖直圆轨道上的A点滑向B点，由于摩擦力的作用，木块的速率保持不变，则在这个过程中
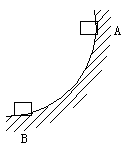
图4
A. 木块的加速度为零
B. 木块所受的合外力为零
C. 木块所受合外力大小不变，方向始终指向圆心
D. 木块所受合外力的大小和方向均不变
12. 某人从一定高度平抛一物体，抛出时的初速度大小为，物体着地的末速度大小为
，不计空气阻力，则物体在空中的飞行时间为（ ）
A. 
B.
C. 
D.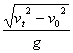 
二. 填空题：本大题共9小题，共20个空，每空2分，共40分。
13. 一个做匀速圆周运动的物体，若半径保持不变，当它的转速变为原来的4倍时，它的线速度将变为原来的______倍，它所受的向心力将变为原来的_______倍；若线速度保持不变，当角速度变为原来的4倍时，它的轨道半径将变为原来的_______倍，它所受的向心力将变为原来的_______倍。
14. 如图5所示，水平地面AB右侧是倾角为的斜面BC，在斜面顶端B处放一小物体，在水平面上方高h处水平抛出一石块，要使石块以平行于斜面的速度击中物体，则抛出点到B点的水平距离s =______，石块的初速度大小为_________。
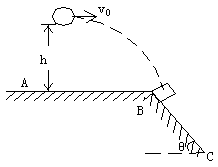
图5
15. 质量为4吨的汽车以10
的速度在水平路面上匀速行驶时对地面的压力是______N，该汽车以同一速率驶过半径是40m的凸形桥顶时对桥面的压力是_______N。（g取
）
16. 地球绕太阳公转的周期为T1，轨道半径为R1，月球绕地球公转的周期为T2，轨道半径为R2，则太阳的质量是地球的质量的______倍。
17. 已知地球的半径约为
，又知月球绕地球的运动可以近似看作匀速圆周运动，则可估算出月球到地心的距离为_________m。（结果保留一位有效数字）
18. 如图6所示，小球质量为m，大小不计，右边圆轨道半径为R，小球从
处沿斜轨滑下后，又沿圆轨道滑到最高点P处，在这一过程中，重力对小球所做的功为 ，小球重力势能减少了 。
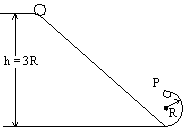
图6
19. 质量为
的钢球，从离地面
高处自由下落
，内钢球重力势能减少了
J（
）（选取地面为参考平面），末钢球的重力势能为 J；如果选取地面上
处的平面为参考平面，末它的重力势能为 J；如果选取自由下落的出发点所在平面为参考平面，末重力势能为 J。
20. 一物体做竖直上抛运动，初速度为，当物体上升的高度为 时，其动能是重力势能的一半，（以抛出点为零势能面）。
21. 质量
的物体静止在地面上，现用120N的竖直拉力提升物体，g取，在重物上升
时，拉力做功 J，物体动能增加 J，重力势能增加 J。
三. 计算题：本大题共3小题，每小题8分，要求写出必要的解题步骤及文字叙述。
22. 长为R的轻杆一端固定一质量为m的小球，以另一端为固定转轴，使之在竖直平面内做圆周运动。求以下两种情况，小球在最高点的速度各为多少？
（1）在最高点时，小球对杆的压力为
（2）在最高点时，小球对杆的拉力为
23. 如果地球自转速度加快到使赤道上的物体对地面正好没有压力，地球半径为R，地球表面的重力加速度为g，求地球的自转角速度？
24. 起重机以
的力，将质量为的物体匀减速地沿竖直方向提升h高度，则起重机钢索的拉力对物体做的功多少？物体克服重力做功为多少？物体的重力势能变化了多少？（空气阻力不计）
【试题答案】
一.
1. C 2. A 3. A 4. B 5. C 6. CD 7. ABC 8. AC
9. A 10. B 11. C 12. D
二.
13. 4，16，
，4 14. 2
15. 
，
16. 
17. 
18.
；
19. 250；
；
；
20. 
21. 1200；200；1000
三.
22. ①
② 
23. 
24. 
；
；增加