高一物理力学竞赛

2002年嘉兴市高中力学竞赛试题卷

考生须知：时间150分钟，ｇ取10ｍ／ｓ²(题号带25的题今年不要求, 题号带△的题普通中学做)

一．　　　  单选题（每题5分）

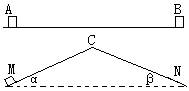△1.如图所示，一物体以一定的初速度沿水平面由A点滑到B点，摩擦力做功为W₁；若该物体从M点沿两斜面滑到N，摩擦力做的总功为W₂。已知物体与各接触面的动摩擦因数均相同，则：

A．W₁＝W₂　　　　　B．W₁＜W₂

C．W₁＞W₂　　　　　D．无法确定

△2.下面是一位科学家的墓志铭：　　　　　　爵士安葬在这里。他以超乎常人的智力第一个证明了行星的运动与形状、彗星的轨道和海洋的潮汐。他孜孜不倦地研究光线的各种不同的折射角，颜色所产生的种种性质。对于自然、历史和圣经，他是一个勤勉、敏锐的诠释者。让人类欢呼，曾经存在过这样一位伟大的人类之光。这位科学家是：

A．开普勒　　　　　 B．牛顿　　　　C．伽利略　　　 　D．卡文迪许

3.2002年3月25日，北京时间22时15分，我国在酒泉卫星发射中心成功发射了一艘正样无人飞船，除航天员没有上之外，飞船技术状态与载人状态完全一致。它标志着我国载人航天工程取得了新的重要进展，为不久的将来把中国航天员送上太空打下了坚实的基础。这飞船是

A．北斗导航卫星　　　B．海洋一号　　C．风云一号D星　　D．神舟三号

4.如图所示，有一箱装得很满的土豆，以一定的初速度在动摩擦因数为μ的水平地面上做匀减速运动，不计其它外力及空气阻力，则中间一质量为ｍ的土豆A受到其它土豆对它的总作用力大小应是：

A．μmg　　　　　　 B．mg

C．mg 　　　 D．mg

5.如图所示，B、C、D、E、F五个球并排放置在光滑的水平面上，B、C、D、E四个球质量相同，均为m=2kg，A球质量等于F球质量，均为m=1kg，现在A球以速度v₀向B球运动，所发生的碰撞均为弹性碰撞，则碰撞之后：

A．五个球静止，一个球运动　　　　　 B. 四个球静止，二个球运动

C．三个球静止，三个球运动　　　　　 D．六个球都运动

6．一物体原来静置于光滑的水平面上。现对物体同时施加两个方向水平、互成120°角的等大的力，作用时间为t，物体的瞬时速度大小为v；之后，撤去其中一个力，并保持另一力大小方向不变，再经时间t，物体的瞬时速度大小为：

A．v　　　　  B．v　　　　　 C．2v　　　　　 D．3v

7．科学家们使两个被加速后的带正电的重离子沿同一条直线相向运动而发生猛烈碰撞，试图用此模拟宇宙大爆炸初期的情境。为了使碰撞前的动能尽可能多地转化为内能，关键是设法使这两个重离子在碰撞前的瞬间具有：

A．相同的速率　　　　　　　　　　　 B．相同大小的动量

C．相同的动能　　　　　　　　　　　 D．相同的质量

二．　　　　　  填空题(每空10分)

△8．上海外滩气象信息台需要整体移位，施工人员将信息台与地面脱离后，在信息台与地面之间铺上石英砂，用四个液压机水平顶推。已知信息台质量为4×10⁵kg，假设信息台与地面之间的动摩擦因数为0.2，信息台做的是匀速直线运动，每台液压机的推力相同，若顶推的位移是14m，则每台液压机对信息台做的功是

　　J．

△9．航空母舰上的飞机跑道长度是有限的。飞机回舰时，机尾有一个钩爪，能钩住舰上的一根弹性钢索，利用弹性钢索的弹力使飞机很快减速。若飞机的质量为M=4.0×10³kg，回舰时的速度为v=160m/s，在t=2.0s内速度减为零，弹性钢索对飞机的平均拉力F=　　 N。(飞机与甲板间的摩擦忽略不计)

△10．风能是一种环保型能源。目前全球风力发电的总功率已达7.00×10⁹W，我国约为1.00×10⁸W。某地强风速约为v=20m/s，设该地的空气密度ρ=1.3kg/m³，如果把截面S=20m²的风的动能全部转化为电能，利用上述已知量计算出电功率为

　　　 W．

△11．利用水滴下落可以粗略测出重力加速度g。调节水龙头，让水一滴一滴地流出，在水龙头的正下方放一个盘子，调节盘子的高度，使一个水滴碰到盘子时恰好有一水滴从龙头开始下落，而空中还有一个正在下落中的水滴，测出水龙头到盘子距离为h(m)，再用秒表测时间，以第一个水滴离开水龙头开始计时，到第N个水滴落至盘中共用时间T(s)，则重力加速度g=　　　　m/s²。

△12．一圆柱形鸟笼内养一只小松鼠，若以圆柱形的中心轴线为转轴，突然使笼转动起来，小松鼠受惊后逃上侧壁。当转速加大到一定程度后，小松鼠将爪松开而松鼠不会离开侧壁滑下，设鸟笼横截面的半径为R=0.25m，松鼠与侧壁间的动摩擦因数μ=0.4，则松鼠松爪后不从侧壁滑下的最小线速度是　　  m/s。

13．洪灾是不幸的，发了洪水就要把灾民及时转移。假设某江河宽为h，发洪水时，水的流速为v，某居民点的下游s处是危险水域，为了把灾民及时转移至对岸安全地区，问从该居民点出发的船只的划行速度(相对水)至少　　　 ，才能安全到达对岸。

14．星球的逃逸速度(即第二宇宙速度)为第一宇宙速度的倍。在目前天文观测范围内，宇宙的平均密度为10^-27 kg/m³，如果认为我们的宇宙是这样一个均匀大球体，其密度使得它的逃逸速度大于光在真空中的速度c(即为“黑洞”)，则宇宙的半径至少为　　　　光年(取1光年≈10¹⁶m，结果取一位有效数字)

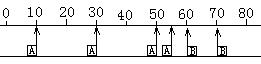15．A、B两滑块在同一光滑的水平直导轨上相向运动发生碰撞(碰撞时间极短可忽略不计)，用闪光照相，闪光4次摄得的闪光照片如下图所示，已知闪光间隔为Δt，而闪光本身持续的时间极短，可忽略不计。在这4次闪光的瞬间，A、B二滑块均在0----80cm刻度范围内，且第一次闪光时，滑块A恰好自左向右通过x=55cm处，滑块B恰好自右向左通过x=70cm处，则A、B两滑块的质量之比m _A∶m_B=　 

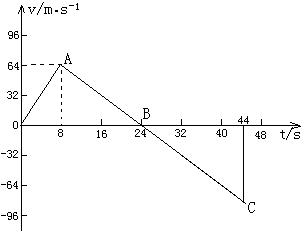
16．一行星探测器从所探测的行星表面垂直升空，假设探测器质量恒为1500kg，发动机推动力为恒力，探测器升空途中发动机突然关闭，质量不变时探测器速度随时间的变化情况如图所示。事实上尽管发动机推动力不变，但由于燃料的消耗，探测器的质量是减少的。假设探测器升空后8s关闭发动机，试在答题卷的坐标图上再画一根速度随时间变化的图线(草图)，并在草图上标出与前面A、B、C三点相应的点A′、B′、C′的位置。

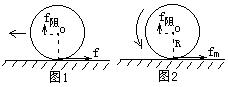17．常规制动系统在急刹车时，车轮常会被抱死，即车轮只滑不转，车轮受力情况如图1所示。装有ABS的汽车在刹车过程中ABS使车轮在地面上滚动而不滑动，车轮受力情况如图2所示。已知质量为m，车轮与地面的动摩擦因数为μ，车轮与地面间的最大静摩擦力为f_m的汽车。在两种情况下行驶的速度相同，则不装ABS系统的刹车距离为S₁，装ABS系统后的刹车距离为S₂，这两者距离之差是S₁-S₂=　　　。

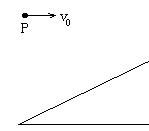
18．如图所示，一质点从P点开始作平抛运动，已知质点与图中斜面发生垂直碰撞，请在答题卷的图中作出质点与斜面发生垂直碰撞的位置(作图要求精确)。

19．已知排球场双场地的总长为18m，设网高为2m。当排球队员站在底线跳起进行发球时，如果球是水平击出的，不考虑球的旋转，当击球点的高度等于某个值时球擦网又恰好没越界，则这一高度为　　　　m。

20．所谓飞车走壁，实际上车子是飞驰在一个高8.60m，底部和顶部直径分别为9.10m和11.68m的圆台形的大木桶内壁上的特技表演。当杂技员车速为18m/s，车轮和桶壁垂直，此时飞车在半径为　　　 m的圆台形木桶内壁上做匀速圆周运动。

三．　　　　　  计算题(每题15分)

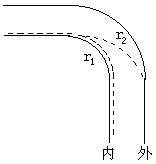
△21．如图所示，赛车在水平赛道上做90°转弯，其内、外车道转弯处的半径分别为r₁、r₂，车与路面间的动摩擦因数都是μ。试问：竞赛中车手应选图中的内道还是外道转弯？在上述两条转弯路径中，车手在内、外车道选择中可能赢得的时间为多少？

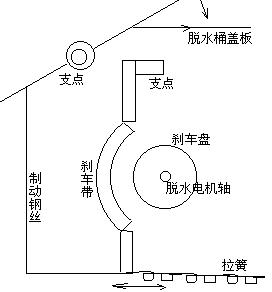△22．普通洗衣机的竖直脱水桶以1200r/min的速度高速旋转(图中未画出脱水桶)，为避免发生人身伤害事故，脱水机构都装有安全制动系统，该系统由脱水桶盖板、制动钢丝、刹车制动盘等组成。当脱水桶运转时，如果打开脱水桶盖，则该系统便产生制动作用。安全制动系统的作用有两个：一是将脱水电动机的电源自动切断；二是制动器中的刹车带自动刹车盘，使脱水桶迅速停止转动。如图所示为脱水制动示意图，若脱水桶的半径为9cm(未画出)，刹车盘的半径为6cm，打开脱水桶盖到脱水桶停止共转了50圈(设为均匀减速)，若衣服和桶的质量为3kg(可以认为质量全部分布在脱水桶桶壁上)。计算刹车带上的平均摩擦力的大小。

23．开普勒从1609—1619年发表了著名的开普勒行星三定律：

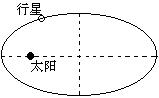　　第一定律：所有的行星围绕太阳运动的轨道都是椭圆，太阳在所有椭圆的一个焦点上；

　　第二定律：太阳和行星的连线在相等的时间内扫过相等的面积；

第三定律：所有行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。

请你用所学力学知识和开普勒第一、第二定律证明开普勒第三定律，结论为：

a³/T²=GM/4π²(其中椭圆的半长轴为a；行星公转的周期为T；太阳质量为M；引力常量为G；引力势能为-GMm/r)

24.如图，一个质量为m的圆环套在一根固定的水平直杆上环与杆的动摩擦因数为μ，现给环一个向右的被速度v₀，如果环在运动过程中还受到一个方向始终竖直向上的力F的作用，已知F=kv，(k为常数，v为速度)，试讨论在环的整个运动过程中克服摩擦力所做的功。(假设杆足够长，分F=mg，F＜mg，F＞mg三种情况)　　

25.如图所示，一块足够长的木板，放在光滑水平面上，在木板上自左向右放有序号是1、2、3……，ｎ的木块，所有木块质量均为ｍ，与木块间的动摩擦因数都相同。开始时，木板静止不动，第1、2、3……、ｎ号木块的初速度分别是ｖ₀、2ｖ₀、3ｖ₀……、ｎｖ₀，方向向右，木板质量与所有木块的总质量相等。最终所有木块与木板以共同速度匀速运动，设木块之间均无相互碰撞。通过分析与计算说明第ｋ号（ｋ＜ｎ＝木块的最小速度。

2002年高中力学竞赛试卷答案

一、单选题：（每题5分，共35分）

1、A　　2、B　　3、D　　4、B　　5、C　　6、B　　7、B

二、填空题（每空10分）

8、2.8×10⁶　　9、3.2×10⁵　　　 10、1.04×10⁵或1.0×0⁵　  11、2Hn²/T²

12、2.5　　　 13、　　14、410¹⁰　　　 15、2/3

16、(1)、OA^/是曲线 （2分），

且A^/ 在A点正上方某处（2分）

(2)、A^/C^/∥AC　(3分)

（3）、C^/点在C正下方侧　(3分)

17、mv²(f_m―f_S)∕f_m·f_S

18、PA垂直斜面（3分）

^{AB垂直地面（3分）}

　　C为中点　 （3分）

　　连接PC延长线交斜面于D点（1分）

19、　　　　20、4.86

三、计算题（每题15分，共45分）

21、解：对外车道，其走弯道所允许的最大车速为V₂，则m(V₂)²∕r₂=μmg,　

∴V₂＝,因此车先减速再加速，加速度为a=μmg∕m=g,减速的路径长为X₂＝（V_m²－V₂²）∕2a=, ∴总时间为t₂=t_减速＋t_圆弧＋t_加速＝+＋（每项2分）＝－（2－）　　 （2分）

同理，车走内道的时间为t₁=－（2－）　　  (4分)

又由于车在内道和外道的直线路径是相等的。∴车手应该选择走外道。时间差为:

Δt=t₁-t₂=（2－）　　(3分)

22、解：脱水后，衣服紧贴脱水桶壁，桶和衣服具有动能，刹车后，动能转化为内能。由动能定理：

　　　　　　 fs=mv²　　 ①　　　　　 （2分）

由线速度关系有：　V＝R　　　　②　　　　　 （2分）

　　　　　　　　　＝2πn　　　 ③　　　　　 （2分）

通过的距离　　　　 s=2πrN　　　　④　　　　　 （2分）

联立①②③④得：f=　 ⑤　　　　  （4分）

把N＝50圈，n=20 r/s,　＝2πn, R=0.09m,　r=0.06m带入⑤得f=10.2N　　 （3分）

23、解：由开普勒第一定律，设行星的近地端、远地端与太阳的距离分别为r_A、r_B，运行速度分别为v_A、v_B, 长轴为a，短轴为b,焦距由开普勒第二定律得：

r_Av_A＝ r_B v_B ①  （3分）

又由行星运动时机械能守恒得：mv_A²―G=mv_B²―G　  ②　 (3分)

由①②得：v_A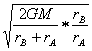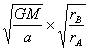＝＝　　  （3分）

∵r_A r_B＝（a－c）（a＋c）=a²－b²

∴T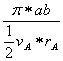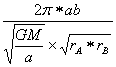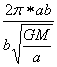＝＝=＝　　 （3分）

∴=　　  （3分）

24、解：（1）若kV₀=mg, 则N＝0，故f=0, 所以 W_f =0　 (3分)

　　　 （2）若kV₀<mg, 则有N+kv=mg,, 则N向上且随着速度的减小而增大，f也将增大，环最终将静止，W_f=mv₀²/2　　　(4分)

　　　　（3）若kV₀>mg, 则有N＋mg=kv, 则N一开始向下且随着速度的减小而减小，当N＝0时，f=0, 环最终将做匀速运动且v=mg/k　　(2分)

由动能定理，W_f＝m(v₀²－v²)/2　　　　 (3分)

　　　　　　  ＝mv₀²/2－m³g²/2k²　　 (3分)

25、解：木块在木板上滑行时均做匀减速运动，且具有相同的加速度，在相同的时间内速度变化、动量变化都相等，而木板开始一直做加速运动。由此可以判断，与木板保持相对静止的木块依次为1、2、3………、n。所以，k号木块的最小速度等于它刚好与木板相对静止时的速度，这时，1——k号木块以及木板有相同的速度，设为V_K，从开始到此时：

1—  —k号木块以及木板的动量变化为：

Δp₁＝m(V_k－V₀)+ m(V_k－2V₀)+ m(V_k－3V₀)+………+ m(V_k－kV₀)+ nmV_k

＝kmV_k－（1＋2＋3＋……＋k）m V₀+nmV_k

＝（k+n）mV_k－m V₀ k（k+1）/2　　　 (5分)

　 而k+1——n号每一个木块的动量变化与k号木块的动量变化相同，均为m(V_k－kV₀),所以k+1——n号木块的动量变化为：

Δp₂＝（n－k）m(V_k－kV₀)　　　　　　　 (5分)

  由动量守恒，得：

Δp₁＋Δp₂＝（k+n）mV_k－m V₀ k（k+1）/2＋（n－k）m(V_k－kV₀)＝0　　（2分）

  可以解得：V_k＝（2n－k＋1）kV₀/4n　　　　　  (3分)