第四章 《牛顿运动定律》
本章的概念包括：
1. 牛顿第一定律
A. 牛顿物理学的基石——惯性定律
B. 惯性与质量
2. 实验：探究加速度与力、质量的关系
C. 加速度与力的关系 D. 加速度与质量的关系
3. 牛顿第二定律
E. 牛顿第二定律—— 
F. 力的单位—— 
4. 力学单位——国际单位制：SI
G. 力学的基本单位 ① 长度：米 ② 质量：千克 ③ 时间：秒
H. 国际单位制（包括：长度、质量、时间、）还有电流、热力学温度、物质的量、发光强度
5. 牛顿第三定律
I. 作用力和反作用力 J. 牛顿第三定律
6. 用牛顿定律解决问题（一）
K. 从受力确定运动情况 L. 从运动情况确定受力
7. 用牛顿定律解决问题（二）
M. 共点力的平衡条件 N. 超重和失重
分类试题汇编
一、选择题
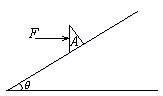1．质量为m的三角形木楔A置于倾角为
的固定斜面上，它与斜面间的动摩
擦因数为
，一水平力F作用在木楔A的竖直平面上，在力F
的推动下，木楔A沿斜面以恒定的加速度a向上滑动，则F的
大小为：
A．
B．
C．
D．
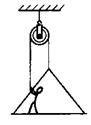2．跨过定滑轮的绳的一端挂一吊板，另一端被吊板上的人拉住，如图
所示，已知人的质量为70kg，吊板的质量为10kg，绳及定滑轮的质
量、滑轮的摩擦均可不计。取重力加速度g=10m/s2。当人以440N的
力拉绳时，人与吊板的加速度a和人对吊板的压力F分别为
A. a=1.0m/s2, F=260N B. a=1.0m/s2,F=330N
C. a=3.0m/s2 F=110N D. a=3.0m/s2 F=50N
3．根据牛顿运动定律，以下选项中正确的是
A 人只有在静止的车厢内，竖直向上高高跳起后，才会落在车厢的原来位置。
B 人在沿直线匀速前进的车厢内，竖直向上高高跳起后，将落在经起点的后方
C 人在沿直线加速前进的车厢内，竖直向上高高挑起后，将落在起跳点的后方
D 人在沿直线减速前进的车厢内，竖直向上高高跳起后，将落在起跳点的后方
4．三个完全相同的物块1、2、3放在水平桌面上，它们与桌面间的动摩擦因数都相同。现用大小相同的外力F沿图示方向分别作用在1和2上，用
的外力沿水平方向作用在3上，使三者都做加速运动。令a1、a2、a3分别代表物块1、2、3的加速度，则
A．a1=a2=a3 B．a1=a2,a2>a3 C．a1>a2,a2<a3 D．a1>a2,a2>a3
5．下列哪个说法是正确的？
A．体操运动员双手握住单杠吊在空中不动时处于失重状态；
B．蹦床运动员在空中上升和下落过程中都处于失重状态；
C．举重运动员在举起杠铃后不动的那段时间内处于超重状态；
D．游泳运动员仰卧在水面静止不动时处于失重状态。
6．放在水平地面上的一物块，受到方向不变的水平推力F的作用，F的大小与时间t的关系和物块速度v与时间t 的关系如图所示。取重力加速度g＝10m/s2。由此两图线可以求得物块的质量m和物块与地面之间的动摩擦因数μ分别为
 |
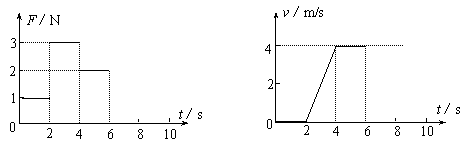A．m＝0.5kg，μ＝0.4
B．m＝1.5kg，μ＝
C．m＝0.5kg，μ＝0.2 D．m＝1kg，μ＝0.2
7．行车过程中，如果车距不够，刹车不及时，汽车将发生碰撞，车里的人可能受到伤害，为了尽可能地减轻碰撞引直怕伤害，人们设计了安全带。假定乘客质量为70 kg，汽车车速为108 km/h（即30 m/s），从踩下刹车到车完全停止需要的时间为5 s，安全带对乘客的作用力大小约为
A．400N B.600N C.800N D.1000N
8．一汽车在路面情况相同的公路上直线行驶，下面关于车速、惯性、质量和滑行路程的讨论，正确的是
Ａ．车速越大，它的惯性越大
Ｂ．质量越大，它的惯性越大
Ｃ．车速越大，刹车后滑行的路程越长
Ｄ．车速越大，刹车后滑行的路程越长，所以惯性越大
9．有两个共点力，F1=2N，F2=4N，它们的合力F的大小可能是
A.1N B.5N C.7N D.9N
10．一质量为m的人站在电梯中，电梯加速上升，加速大小为
，g为重力加速度。人对电梯底部的压力为
A．
B．2mg
C．mg
D．
11．如图所示，位于光滑固定斜面上的小物块P受到一水平向右的推力F的作用。已知物块P沿斜面加速下滑。现保持F的方向不变，使其减小，则加速度
A．一定变小 B．一定变大
C．一定不变 D．可能变小，可能变大，也可能不变
l2．如图所示，一物块位于光滑水平桌面上，用
一大小为F 、方向如图所示的力去推它，使它以加速度a右运动。
若保持力的方向不变而增大力的大小，则
A . a 变大 B .不变
C．a变小 D . 因为物块的质量未知，故不能确定a变化的趋势
13．质量不计的弹簧下端固定一小球。现手持弹簧上端使小球随手在竖直方向上以同样大小的加速度a(a＜g)分别向上、向下做匀加速直线运动。若忽略空气阻力，弹簧的伸长分别为x1、x2；若空气阻力不能忽略且大小恒定，弹簧的伸长分别为
、
。则
A．
B．
C．
D．
二、填空题
1．1999年11月20日我国成功发射和回收了“神舟”号实验飞船，标志着国
的运载火箭技术水平已跻身于世界先进行列。
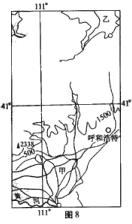
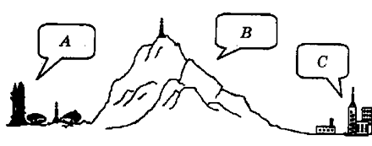图中A为某火箭发射场，B为山区，C为城市。发射场正在进行某型号火箭的发射实
验。该火箭起飞时质量为2.0×106Kg，起飞推力2.75×106N，火箭发射塔高100m，则该火箭起飞时的加速度大小为
m/s2，在火箭推力不变的情况下，若不考虑空气阻力及火箭质量的变化，火箭起飞后，经
秒飞离火箭发射塔。（参考公式及常数：
=ma，vt=v0+at，s=v0t+(1/2)at2，g=9.8m/s2）
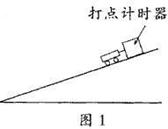
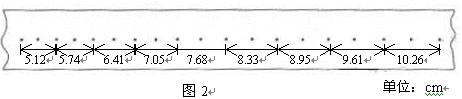
2．一打点计时器固定在斜面上某处，一小车拖着穿过打点计时器的纸带从斜面上滑下，如图1所示，图2是打出的纸带的一段.
（1）已知打点计时器使用的交流电频率为50Hz，利用图2给出的数据可求出小车下滑
的加速度a= .
（2）为了求出小车在下滑过程中所受的阻力，还需测量的物
理量有
用测得的量及加速度a表示阻力的计算式为
=
.
3．2003年10月，神舟五号载人航天飞船成功发射并顺利返回，标志着我国已经成为载人航天技术大国，这是中国人数千年飞天梦想的实现。
飞船降落过程中，在离地面高度为h处速度为v0，此时开动反冲火箭，使船开始做减速运动，最后落地时的速度减为v。若把这一过程当作为匀减速运动来计算，则其加速度的大小等于 。
已知地球表面处的重力加速度为g，航天员的质量为m，在这过程中航天员对坐椅的压力等于 。
三、计算题
1．蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动
作的运动项目。一个质量为60Kg的运动员，从离水平网面3.2m高处自由下落，着网后沿竖直方向蹦回到离水平网面5.0m高处。已知运动员与网接触的时间为1.2s，若把在这段时间内运动员的作用力当作恒力处理，求此力的大小。（g=10m/s2）
【解】将运动员看作质量为m的质点，从h1高处下落，刚接触网时速度的大小
(向下)
弹起后到达的高度h2，刚离开网时速度的大小 
（向上）
速度的改变量 
(向上)
以a表示加速度，
表示接触时间，则 
接触过程中运动员受到向上的弹力F和向下的重力mg。由牛顿第二定律，
F－mg=ma
由以上五式解得，
代入数值得 F=1.5×103N
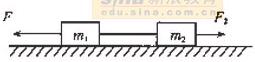2． 如图所示，两个用轻线相连的位于光滑水平面上的物块，质量分别为m1和m2，拉力F1和F2方向相反，与轻线沿同一水平直线，且F1>F2。试求在两个物块运动过程中轻线的拉力T。
【解】 设两物块一起运动的加速度为a,则有
F1－F2=(m1+m2)a ①
根据牛顿第二定律，对质量为m1的物块有F1－T=m1a ②
由①、②两式得
③
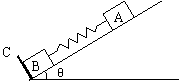3．如图所示，在倾角为θ的光滑斜面上有两个用轻质弹簧相连接
的物块A 、B ．它们的质量分别为mA、mB，弹簧的劲度系数为k , C为一固定挡板。系统处于静止状态。现开始用一恒力F沿斜面方向拉物块A 使之向上运动，求物块B 刚要离开C时物块A 的加速度a 和从开始到此时物块A 的位移d。重力加速度为g。
【解】 令x1表示未加F时弹簧的压缩量，由胡克定律和牛顿定律可知
mAgsinθ=kx1 ①
令x2表示B 刚要离开C时弹簧的伸长量，a表示此时A 的加速度，由胡克定律和牛顿定律可知 kx2=mBgsinθ ②
F－mAgsinθ－kx2=mAa ③
由② ⑧ 式可得a= ④
由题意 d=x1+x2 ⑤
由①②⑤式可得d= ⑥
4．【03江苏】实验装置如图1所示：一木块放在水平长木板上，左侧栓有一细软线，
跨过固定在木板边缘的滑轮与一重物相连。木块右侧与打点计时器的纸带相连。在重物牵引下，木块在木板上向左运动，重物落地后，木块继续向左做匀减速运动，图2给出了重物落地后，打点计时器在纸带上打出的一些点，试根据给出的数据，求木块与木板间的摩擦因数μ。要求写出主要的运算过程。结果保留2位有效数字。（打点计时器所用交流电频率为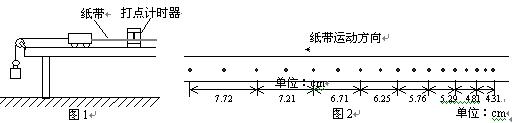
50Hz，不计纸带与木块间的拉力。取重力加速度g=10m/s2）
【解】 由给出的数据可知，重物落地后，木块在连续相等的时间T内的位移分别是：
s1＝7.72cm， s2＝7.21cm， s3＝6.71cm， s4＝6.25cm,
s5＝5.76cm， s6＝5.29cm， s7＝4.81cm， s8＝4.31cm，
以a表示加速度，根据匀变速直线运动的规律，有
△s=
[(s5－s1)+(s6－s2)+(s7－s3)+(s8－s4)]＝4aT2
又知 T=0.04s 解得 a=－3.0m/s2
重物落地后木块只受摩擦力的作用，以m表示木块的质量，根据牛顿定律，有
－μmg=ma 解得：μ=0.30
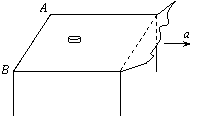5．一小圆盘静止在桌布上，位于一方桌的水平桌面的中央。桌布的一边与桌的AB边重合，如图。已知盘与桌布间的动摩擦因数为 μ1，盘与桌面间的动摩擦因数为 μ2。现突然以恒定加速度a将桌布抽离桌面，加速度方向是水平的且垂直于AB边。若圆盘最后未从桌面掉下，则加速度a满足的条件是什么？(以g表示重力加速度)
【解】 对盘在桌布上有 μ1mg = ma1 ①
在桌面上有μ2mg = ma2 ②
υ12 =2a1s1 ③
υ12
=2a2s2
④
盘没有从桌面上掉下的条件是s2≤1 l
- s1
⑤
对桌布 s = 1 at2 ⑥
对盘 s1 = 1 a1t2
⑦
而 s = 1 l
+ s1 ⑧
由以上各式解得a≥( μ1 + 2 μ2) μ1g/ μ2 ⑨
6．一质量为m＝40kg的小孩子站在电梯内的体重计上。电梯从t＝0时刻由静止开始上升，在0到6s内体重计示数F的变化如图所示。试问：在这段时间内电梯上升的高度是多少？取重力加速度g＝10m/s2。
【解】 由图可知，在t＝0到t＝t1＝2s的时间内，体重计的示数大于mg，故电梯应做向上的加速运动。设这段时间内体重计作用于小孩的力为f1，电梯及小孩的加速度为a1，由牛顿第二定律，得f1－mg＝ma1 ①
在这段时间内电梯上升的高度h1＝a1t2。 ②
在t1到t＝t2＝5s的时间内，体重计的示数等于mg，故电梯应做匀速上升运动，速度为t1时刻电梯的速度，即V1＝a1t1， ③
在这段时间内电梯上升的高度h2＝V2（t2－t1）。 ④
在t2到t＝t3＝6s的时间内，体重计的示数小于mg，故电梯应做向上的减速运动。设这段时间内体重计作用于小孩的力为f1，电梯及小孩的加速度为a2，由牛顿第二定律，得
mg－f2＝ma2， ⑤
在这段时间内电梯上升的高度h3＝V1(t3－t2)－a 2(t3－t2)2。 ⑥
电梯上升的总高度h＝h1＋h2＋h3。 ⑦
由以上各式，利用牛顿第三定律和题文及题图中的数据，解得h＝9 m。 ⑧
7．【06全国I】 一水平的浅色长传送带上放置一煤块（可视为质点），煤块与传送带之间的动摩擦因数为。初始时，传送带与煤块都是静止的。现让传送带以恒定的加速度
开始运动，当其速度达到
后，便以此速度做匀速运动。经过一段时间，煤块在传送带上留下了一段黑色痕迹后，煤块相对于传送带不再滑动。求此黑色痕迹的长度。
【解】 根据“传送带上有黑色痕迹”可知，煤块与传送带之间发生了相对滑动，煤块的加速度a小于传送带的加速度ao。根据牛顿定律，可得 a = μg ①
设经历时间t，传送带由静止开始加速到速度等于vo，煤块则由静止加速到v，有
vo = aot ②
v = at ③
由于a<ao，故v<vo煤块继续受到滑动摩擦力的作用。再经过时间t′，煤块的速度由v增加到vo，有 vo = v+at′ ④
此后，煤块与传送带运动速度相同，相对于传送带不再滑动，不再产生新的痕迹。
没有煤块的速度从0增加到vo的整个过程中，传送带和煤块移动的距离分别为so和s，有
So =
aot2+vot′ ⑤
⑥
传送带上留下的黑色痕迹的长度 
= so-s
⑦
由以上各式得 
⑧
参 考 答 案
一、选择题
1．C 2． B 3．C 4．C 5．B 6．A 7．A
8．AC 9．B 10．D 11．B l2．A 13．A
二、填空题
1． 3.81 m/s2； 7.25s（答3.83s同样给分）
2．（1）4.00m/s2 (3.90~4.10m/s2之间都正确)
（2）小车质量m；斜面上任意两点是距离及这两点的高度差h. 
3．
