机 械 振 动 单 元 测 试
一、单项选择题（每小题只有一个选项附合题意，请将该选项填入下列答题卡的表格中）
选择题答卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
|
|
|
|
|
|
| 题号 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
1. 作简谐运动物体, 在每次通过同一位置时, 动量、动能、速度、加速度四个量中，总是相同的量是：
A.速度和动量 B.加速度与动能
C.速度、动量和加速度 D.动量、动能、速度、加速度
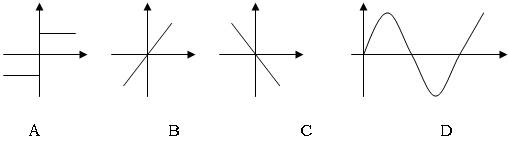
2．在下图中，能正确表示质点做简谐振动时所受外力跟位移关系的是：
3、一弹簧振子做周期为0.4s，振幅为5cm的简谐运动，t=0时振子在平衡位置，则在2s内振子的位移大小及通过的路程分别是[ ]
A．0 ，20cm B．0 ，100cm C．5cm ，20cm D．5cm ，100cm
4．如图，是某振子作简谐振动的图象，以下说法中正确的是：
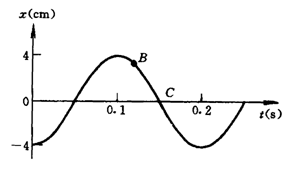A．图象就是振子实际运动的轨迹
B．振子在B位置的位移就是曲线BC的长度
C．该振子的周期为0.2s
D．该振子的振幅为8cm
5．若单摆的摆长不变，使同一单摆通过平衡位置的速度增大一倍，则此单摆做简谐运动的频率和振幅的情况是：
A．频率不变、振幅变大 B．频率不变、振幅减小
C．频率改变、振幅改变 D．频率改变、振幅不变
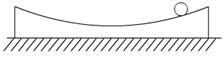
6．一个打磨得很精细的小凹镜，其曲率很小可视为接近平面．将镜面水平放置如图所示．一个小球从镜边缘开始释放，小球在镜面上将会往复运动，以下说法中正确的是：
A．小球质量越大，往复运动的周期越长
B．释放点离最低点距离越大，周期越短
C．凹镜曲率半径越大，周期越长
D．周期应由小球质量、释放点离平衡位置的距离，以及曲率半径共同决定
6．工厂里, 有一台机器正在运转, 当其飞轮转得很快的时候, 机器的振动并不强烈. 切断电源, 飞轮转动逐渐慢下来, 到某一时刻t, 机器发生了强烈的振动, 此后, 飞轮转动得更慢, 机器的振动反而减弱, 这种现象说明 [ ]
A. 在时刻t飞轮惯性最大
B. 在时刻t飞轮转动的频率最大
C.纯属偶然现象, 并无规律
D.在时刻t飞轮转动的频率与机身的固有频率相等, 发生共振
7．单摆在振动过程中，摆动幅度越来越小这是因为：
A．能量正在逐渐消灭
B．动能正在转化为势能
C．机械能守恒
D．总能量守恒，减少的动能转化为内能
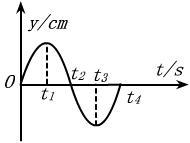8．卡车在公路上行驶，货物随车厢上、下作简谐运动而不脱离底板，设向上为正方向，其振动图线如图所示，由图可知，货物对底板的压力小于货物的重力的时刻是[ ]
A．t1 B．t2 C．t3 D．t4
9．置于同地点的甲、乙两单摆的振动图像如图，下列说法正确的是：
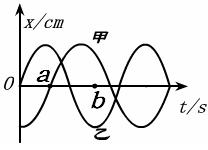A．甲、乙两摆的摆长相等
B．甲球质量小于乙球质量
C．甲摆摆长大于乙摆摆长
D．甲摆在a时刻的重力势能大于b时刻的重力势能
10．如图所示，是物体的受迫振动的共振曲线，其纵坐标表示了物体的:
A．在振动中不同时刻的振幅
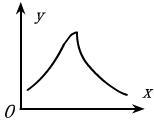B．在振动中不同时刻的位移
C．在不同驱动力频率下的振幅
D．在不同驱动力频率下的位移
11．如图有四个图像，下列说法错误的是
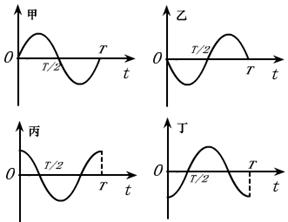A．若甲表示位移，则丙表示速度
B．若甲表示位移，刚乙表示加速度
C．若丁表示位移，则乙表示速度
D．若乙表示速度，则丙表示位移
二、填空和实验：
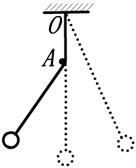13、如图所示，摆长为L的单摆，原来的周期为T。现在在悬点O的正下方A点固定一颗钉子，使OA=L/3，令单摆由平衡位置向左摆动时以A为悬点作简谐振动，则这个摆完成一次全振动所需的时间是
。
14、铁道上每根钢轨长12m，若支持车厢的弹簧固有周期是0.6s，那么列车以 m/s速度行驶时，车厢振动最厉害。
15、某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.50cm，摆球直径为2.0cm，然后用秒表记录了单摆振动50次所用的时间为99.9s．则
①该摆摆长为_______cm，周期为 s
②（单选题）如果他测得的g值偏小，可能的原因是 [ ]
A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时，秒表过迟按下
D．实验中误将49次全振动数为50次
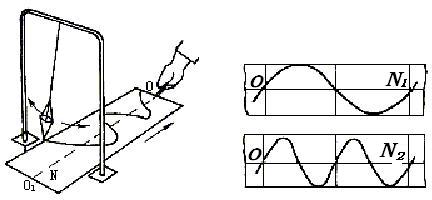
16．如图是演示简谐运动图像的装置，当沙漏斗下面的薄木板N被匀速地拉出时，振动着的漏斗中漏出的沙在板上形成的曲线显示出摆的位移随时间变化的关系．板上的直线OO1代表时间轴，右图中是两个摆中的沙在各自板上形成的曲线，若板N1和板N2拉动的速度v1和v2的关系为v2=2v1，则板N1、N2上曲线所代表的周期T1和T2的关系为:
A．T2=T1． B．T2=2T1． C．T2=4T1． D.T2=T1/4
三、计算和证明：
17．如图，试证明弹簧振子上下振动时的振动为简谐运动．
18．一较长的弹簧两端拴着质量分别为m1和m2的物体，今将m2放于水平面上，缓缓向下加力将m1往下压，如图，m1到最低点时所施压力大小为F．若要求撤去F后m1跳起将m2拉得跳离桌面，F至少多大？
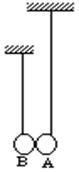
19．如图，A、B两单摆摆长分别为 
、
，两球静止时刚好接触，且重心等高、质量相等。今把A球从平衡位置向右拉开一个微小角度，然后无初速释放，于是AB将发生一系列弹性正碰，设碰撞后两球速度互换，碰撞时间不计．则释放A球后20s内两球碰撞多少次？
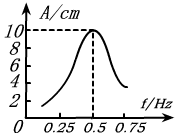
20．右图为一单摆的共振曲线，则该单摆的摆长约为多少？共振时单摆的振幅多大？（g取10m/s2）
参考答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 | B | C | B | C | A | D |
| 题号 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | A | C | C |
|
二、填空题：
13．
14．20 15．98.50，2.00 16．D
三、计算和证明：
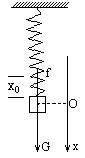17．证明：取x轴正方向向下，在图示平衡位置时，弹簧伸长量为x0，有kx0=mg．
当物体相对平衡位置的位移为x时，弹簧弹力为f=k(x＋x0)，f为正时向上．
回复力为F=mg－f=－kx．
所以是简谐运动，
18．解：设F=F0时，撤去F后m1上升到最高点时m2对地压力为零，此时弹簧伸长量为：x1=m2g/k．
m1上下振动，在平衡位置时弹簧压缩量为：x0=m1g/k．
所以m1振幅为：A=x0+x1=(m1＋m2)g/k．
在最低点，弹簧压缩量为：x0+A=(2m1＋m2)g/k
撤去F前：F0＋m1g=k(x0＋A)
解得：F0=(m1＋m2)g．
∴F应大于F0，即F＞（m1+m2）g．
19．解：先求出AB摆长的单摆周期：
A释放后经
与B发生碰撞，碰后速度交换，A静止，B球向左摆动，再经
又摆回与A发生碰撞，碰后B静止，A向右运动，再经
回到最右边。可见每经过
，A、B发生两次碰撞，A又回到释放初的最右位置。所以有：
20s末A刚好回到平衡位置，第27次碰撞正在发生．
20．解：由图可知，单摆在f驱=0.5Hz时振动最剧烈，表明此时发生了共振，振幅为10cm。
由
，得：L=
=
=1.01m