08届高三物理周考试题十五
一、本题共10小题:每小题5分,共50分。在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。全部选对的得5分,选不全的得3分,有选错或不答的得0分。
1、玻璃茶杯从同一高度掉下,落在水泥地上易碎,落在海绵垫上不易碎,这是因为茶杯与水泥地撞击过程中
A.茶杯的初动量较大 B.茶杯动量变化较大
C.茶杯所受冲量较大 D.茶杯动量变化率较大
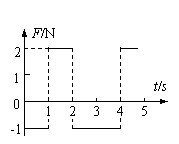
2、物体只在力F作用下运动,力F随时间变化的图像如图所示,在t=1s时刻,物体的速度为零,则下列论述正确的是
A.0~3s内,力F所做的功等于零,冲量也等于零
B.1~4s内,力F所做的功等于零,冲量也等于零
C.第1s内和第2s内的速度方向相同,加速度方向相反
D.第3s内和第4s内的速度方向相反,加速度方向相同
3、在高台跳水中,运动员从高台上向下跃起,在空中完成动作后,进入水中在浮力作用下做减速运动,速度减为零后返回水面.设运动员在空中运动过程为І,在进入水中做减速运动过程为ІІ.不计空气阻力和水的粘滞阻力,则运动员
A.在过程І中,重力的冲量等于动量的改变量
B.在过程І中,重力冲量的大小与过程ІІ中浮力冲量的大小相等
C.在过程І中,每秒钟运动员动量的变化量相同
D.在过程І和在过程ІІ中动量变化的大小相等
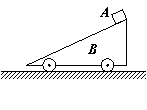 4、一底面带轮子的斜面体B (不计轮与轴之间的摩擦),静止地放在光滑水平面上,一个小物块A从斜面顶端无摩擦地自由滑下,在下滑的过程中
4、一底面带轮子的斜面体B (不计轮与轴之间的摩擦),静止地放在光滑水平面上,一个小物块A从斜面顶端无摩擦地自由滑下,在下滑的过程中
A.A和B组成的系统机械能守恒
B.A和B组成的系统动量守恒
C.B对A的支持力不对A做功
D.A对B的压力对B做正功
5、如图所示,水平地面上放着一个表面均光滑的凹槽,槽两端固定有两轻质弹簧,一弹性小球在两弹簧间往复运动,把槽、小球和弹簧视为一个系统,则在运动过程中:
A.系统的动量守恒,机械能不守恒
![]() B.系统的动量守恒, 机械能守恒
B.系统的动量守恒, 机械能守恒
C.系统的动量不守恒,机械能守恒
D.系统的动量不守恒,机械能不守恒
6、炮弹的质量为m,装好炮弹的大炮总质量为M,炮弹出口时相对地面的速度为v,炮弹与水平方向夹角为α,如果不考虑炮车与水平地面的摩擦,则射击时炮车的后退速度为
A.mv/(M—m) B.mvcosα/M C.mv/M D.mvcosα/(M—m)
7、在光滑的水平面上,有两个静止的小车,车上各站着一个运动员,两车(包含负载的总质量均为M)。设甲车上的人接到一个质量为m,沿水平方向飞来的速率为V的篮球;乙车上的人把原来在车上的同样的篮球沿水平方向以速率V掷出去,则这两种情况下,甲、乙两车所获得的速度大小的关系是(以上速率是相对地面而言)
A.V甲>V乙 B.V甲<V乙
C.V甲=V乙 D.视M、m和V的大小而定
8、只小船静止在湖面上,一个人从小船的一端走到另一端,不计水的阻力,下列说法中正确的是
A.人在船上行走时,人对船的冲量比船对人的冲量小,所以人走得快,船后退的慢
B.人在船上行走时,人的质量比船小,它们所受冲量大小是相等的,所以人向前走得快,船后退得慢
C.人停止走动时,因船的惯性大,所以船将继续后退
D.人停止走动时,因总动量守恒,故船也停止后退
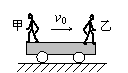 9、如图所示,光滑水平面上有一辆质量为2m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对于地面水平向右的速度u跳离小车,然后站在车左端的甲以相对于地面水平向左的速度u跳离小车,两人都离开小车后,小车的速度将是
9、如图所示,光滑水平面上有一辆质量为2m的小车,车上左右两端分别站着甲、乙两人,他们的质量都是m,开始两个人和车一起以速度v0向右匀速运动.某一时刻,站在车右端的乙先以相对于地面水平向右的速度u跳离小车,然后站在车左端的甲以相对于地面水平向左的速度u跳离小车,两人都离开小车后,小车的速度将是
A.v0 B.大于v0小于2 v0 C. 2 v0 D.大于2 v0
![]() 10、如图所示,质量为M,长为L的长木板放在光滑的水平面上。一个质量也为M的物块(可视为质点)以一定的初速度从左端冲上木板。如果长木板是固定的,物块恰好停在木板的右端;如果长木板不固定,则物块冲上长木板后,相对长木板滑行的距离是
10、如图所示,质量为M,长为L的长木板放在光滑的水平面上。一个质量也为M的物块(可视为质点)以一定的初速度从左端冲上木板。如果长木板是固定的,物块恰好停在木板的右端;如果长木板不固定,则物块冲上长木板后,相对长木板滑行的距离是
A.L B.3 L/4 C.L/2 D.L/4
二、实验题(本题共2小题,共15分)
11、在“验证机械能守恒定律”的实验中,下列说法或做法正确的是
A.选用质量大的重锤可减小实验误差
B.实验结果总是动能增加略大于势能减小
C.固定好打点计时器,用手拿住穿过限位孔的纸带一端,手应静止靠近打点计时器处
D.先松开纸带,再接通电源,重物自由下落时纸带上就能打出一系列点,重复做几次
12、在“验证机械能守恒定律”的实验中,质量为1 kg的重锤自由下落,通过打点计时器在纸带上记录运动过程,打点计时器所接电源为6 V、50 Hz的交流电源,如图1—19—5所示.纸带上O点为重锤自由下落时纸带打点起点,选取的计数点A、B、C、D依次间隔一个点(图中未画出),各计数点与O点距离如图所示,单位为mm,重力加速度为9.80 m/s2,则
(1)打点计时器记录B点时,重锤速度vB=_________m/s,重锤动能EkB=_________J
(2)从开始下落算起,打点计时器记录B点时重锤的重力势能减少__________J
(3)以B点为例,说明你怎样判断重锤下落过程中机械能是否守恒?
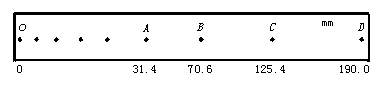
三、解答题(本题共4小题,55分。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题答案中必须明确写出数值和单位。)
13、(12分)用一水平恒力作用于静止在光滑水平地面上的物体,经过4s物体获得100J的动能。若改用一半大小的水平恒力作用于同一物体,则物体由静止运动8m后也可获得100J的动能。则该物体的质量是多大?
14、(12分)质量为M的小船以速度v0行驶,船上有两个质量皆为m的小孩a和b,分别静止站在船头和船尾。现在小孩a沿水平方向以速率v(相对于静止水面)向前跃入水中,然后小孩b沿水平方向以同一速率v(相对于静止水面)向后跃入水中。求小孩b跃出后小船的速度。
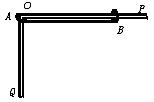 15、(14分)如图所示,质量都为m的A、B两环用细线相连后分别套在光滑细杆OP和竖直光滑细杆OQ上,线长L=0.4 m,将线拉直后使A和B在同一高度上都由静止释放,当运动到使细线与水平面成30°角时,A和B的速度分别为vA和vB,求vA和vB的大小。
15、(14分)如图所示,质量都为m的A、B两环用细线相连后分别套在光滑细杆OP和竖直光滑细杆OQ上,线长L=0.4 m,将线拉直后使A和B在同一高度上都由静止释放,当运动到使细线与水平面成30°角时,A和B的速度分别为vA和vB,求vA和vB的大小。
16、(17分)如图所示,光滑的水平轨道接一个半径为R的光滑半圆轨道,在水平轨道上有2002个质量相同的小球。除第1号小球外,其他小球均静止。第1号小球以初速度v0碰撞第2号小球,在碰撞过程中损失初动能的![]() ;第2号小球碰撞第3号小球,在碰撞过程中损失第2号小球初动能的
;第2号小球碰撞第3号小球,在碰撞过程中损失第2号小球初动能的![]() ;第3号小球又碰撞第4号小球,依次碰撞下去,每次碰撞均损失前一小球初动能的
;第3号小球又碰撞第4号小球,依次碰撞下去,每次碰撞均损失前一小球初动能的![]() ,最后,第2002号小球恰能沿半圆轨道达到最高点。试求第1号小球的初速度v0。
,最后,第2002号小球恰能沿半圆轨道达到最高点。试求第1号小球的初速度v0。

 答题卷
答题卷
一、本题共10小题:每小题5分,共50分。在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确。全部选对的得5分,选不全的得3分,有选错或不答的得0分。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、实验题(共15分)
11、(1)____________ (2)___________
12、(1)_________________ (2)__________________ (3)___________
三、解答题(本题共4小题,55分。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题答案中必须明确写出数值和单位。)

13、(12分)用一水平恒力作用于静止在光滑水平地面上的物体,经过4s物体获得100J的动能。若改用一半大小的水平恒力作用于同一物体,则物体由静止运动8m后也可获得100J的动能。则该物体的质量是多大?
 14、(12分)质量为M的小船以速度v0行驶,船上有两个质量皆为m的小孩a和b,分别静止站在船头和船尾。现在小孩a沿水平方向以速率v(相对于静止水面)向前跃入水中,然后小孩b沿水平方向以同一速率v(相对于静止水面)向后跃入水中。求小孩b跃出后小船的速度。
14、(12分)质量为M的小船以速度v0行驶,船上有两个质量皆为m的小孩a和b,分别静止站在船头和船尾。现在小孩a沿水平方向以速率v(相对于静止水面)向前跃入水中,然后小孩b沿水平方向以同一速率v(相对于静止水面)向后跃入水中。求小孩b跃出后小船的速度。

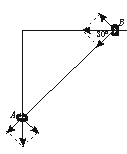
 15、(14分)如图所示,质量都为m的A、B两环用细线相连后分别套在光滑细杆OP和竖直光滑细杆OQ上,线长L=0.4 m,将线拉直后使A和B在同一高度上都由静止释放,当运动到使细线与水平面成30°角时,A和B的速度分别为vA和vB,求vA和vB的大小。
15、(14分)如图所示,质量都为m的A、B两环用细线相连后分别套在光滑细杆OP和竖直光滑细杆OQ上,线长L=0.4 m,将线拉直后使A和B在同一高度上都由静止释放,当运动到使细线与水平面成30°角时,A和B的速度分别为vA和vB,求vA和vB的大小。
 16、(17分)如图所示,光滑的水平轨道接一个半径为R的光滑半圆轨道,在水平轨道上有2002个质量相同的小球。除第1号小球外,其他小球均静止。第1号小球以初速度v0碰撞第2号小球,在碰撞过程中损失初动能的
16、(17分)如图所示,光滑的水平轨道接一个半径为R的光滑半圆轨道,在水平轨道上有2002个质量相同的小球。除第1号小球外,其他小球均静止。第1号小球以初速度v0碰撞第2号小球,在碰撞过程中损失初动能的![]() ;第2号小球碰撞第3号小球,在碰撞过程中损失第2号小球初动能的
;第2号小球碰撞第3号小球,在碰撞过程中损失第2号小球初动能的![]() ;第3号小球又碰撞第4号小球,依次碰撞下去,每次碰撞均损失前一小球初动能的
;第3号小球又碰撞第4号小球,依次碰撞下去,每次碰撞均损失前一小球初动能的![]() ,最后,第2002号小球恰能沿半圆轨道达到最高点。试求第1号小球的初速度v0。
,最后,第2002号小球恰能沿半圆轨道达到最高点。试求第1号小球的初速度v0。

参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | ABC | ACD | AD | B | D | B | BD | C | C |
11、A
12、(1)vB=1.18 m/s;EkB=6.96×10-1 J。
(2)ΔEp=6.92×10-1 J
(3)上述所得ΔEk与ΔEp在误差允许范围内二者相等,验证了物体在只受重力作用时,重力势能的减少量等于动能的增加量,即机械能守恒。
13、解析: 设水平恒力为F,根据动量定理 Ft=mv (1)···············3分
上式两边平方得:(Ft)2=(mv)2=2m![]() (2)···············3分
(2)···············3分
当对物体用力为![]() 时,根据动能定理
时,根据动能定理![]() (3 )···············3分
(3 )···············3分
由(2)(3)联立解得 m=50kg.···············3分
14、解析:因均是以对地(即题中相对于静止水面)的水平速度,所以先后跃入水中与同时跃入水中结果相同。
设小孩b跃出后小船向前行驶的速度为v,取v0为正向,根据动量守恒定律,有
(M+2m)v0=Mv+mv-mv
解得:v=(1+![]() )v0
)v0
15、解析:由图可知:vAsin30°=vBcos30°···············3分
 即vA=
即vA=![]() v ①···············3分
v ①···············3分
A球下落的高度:
h=Lsin30°=0.4×![]() ···············3分
···············3分
h=0.2 m
由机械能守恒定律
mgh=![]() mvA2+
mvA2+![]() mvB2 ②···············3分
mvB2 ②···············3分
联立①②并代入数据得:
vA=![]() m/s,vB=1 m/s···············2分
m/s,vB=1 m/s···············2分
16、解析:设第1号球与第2号球碰后的速度分别为v1和v2
由动量守恒定律得:
mv0=mv1+mv2 ①······························3分
由能量关系可得
![]() ②···············3分
②···············3分
解①②可得v2=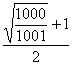 v0···············3分
v0···············3分
由于每次碰撞所遵循的规律完全相同,分析归纳可得
经2001次碰撞后,第2002号球获得的速度为
v2002=(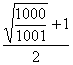 )2001v0 ③···············2分
)2001v0 ③···············2分
因为第2002号球恰能到圆轨道的最高点,所以对第2002号球,根据机械能守恒定律有
![]() mv2+mg·2R ④···············2分
mv2+mg·2R ④···············2分
在最高点有mg=m![]() ⑤···············2分
⑤···············2分
解③④⑤可得第1号球的初速度
v0 ![]() 3.69
3.69![]() ···············2分
···············2分