高考物理第三轮复习力学题易错题
例1、 ①如图1所示,质量为m的物体用细绳OC悬挂在支架上的O点,轻杆OB可绕B点转动,求细绳OA中张力T大小和轻杆OB受力N大小。
分析与解:由于悬挂物体质量为m,绳OC拉力大小是mg,将重力沿杆和OA方向分解,可求![]() .
.
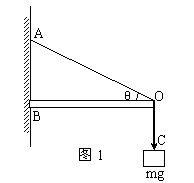
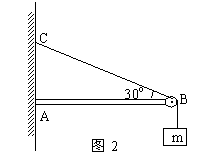
②如图2所示,水平横梁一端A插在墙壁内,另一端装有小滑轮B,一轻绳一端C固定于墙壁上,另一端跨过滑轮后悬挂一质量为m=10kg的重物,![]() ,则滑轮受到绳子作用力为:
,则滑轮受到绳子作用力为:
A. 50N B. ![]() C. 100N
D.
C. 100N
D. ![]()
分析与解:对于②若依照①中方法,则绳子对滑轮![]() ,应选择D项;实际不然,由于杆AB不可转动,是死杆,杆所受弹力的方向不沿杆AB方向。由于B点处是滑轮,它只是改变绳中力的方向,并未改变力的大小,滑轮两侧绳上拉力大小均是100N,夹角为
,应选择D项;实际不然,由于杆AB不可转动,是死杆,杆所受弹力的方向不沿杆AB方向。由于B点处是滑轮,它只是改变绳中力的方向,并未改变力的大小,滑轮两侧绳上拉力大小均是100N,夹角为![]() ,故而滑轮受绳子作用力即是其合力,大小为100N,正确答案是C而不是D。
,故而滑轮受绳子作用力即是其合力,大小为100N,正确答案是C而不是D。
例2、竖直向上抛出一物体,已知其出手时的速度是5m/s,经过3s,该物体落到抛出点下某处,速度为25m/s,已知该物体在运动过程中加速度不变,求该加速度的大小及方向。
错解:由题意知V0=5m/s,Vt=25m/s,所以加速度a=(Vt-V0)/t=6.67m/s2.
分析与解:由于速度是矢量,处理同一直线上的矢量运算,必须先选定正方向,将矢量运算转化为代数运算。
取向上为正方向,由题意知:V0=5m/s,Vt=-25m/s,所以加速度a=(Vt-V0)/t=-10m/s2.
加速度为负,表示加速度的方向与正方向相反,即a的方向竖直向下。
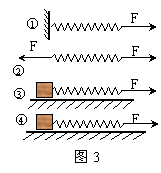 例3、如图3所示,四个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:1中弹簧的左端固定在墙上,2中弹簧的左端受大小也为F的拉力作用,3中弹簧的左端拴一小物块,物块在光滑的桌面上滑动,4中弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动。若认为弹簧的质量都为零,以L1、L2、L3
、L4依次表示四个弹簧的伸长量,则有:
例3、如图3所示,四个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:1中弹簧的左端固定在墙上,2中弹簧的左端受大小也为F的拉力作用,3中弹簧的左端拴一小物块,物块在光滑的桌面上滑动,4中弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动。若认为弹簧的质量都为零,以L1、L2、L3
、L4依次表示四个弹簧的伸长量,则有:
A.L2>L1; B. L4>L3;
C.L1>L3; D. L2=L4.
错解:由于4中弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动,而3中弹簧的左端拴一小物块,物块在光滑的桌面上滑动,所以有 L4>L3,即B选项正确。
分析与解:命题者将常见的四种不同的物理情景放在一起,让学生判别弹簧的伸长量的大小,不少学生不加思考的选择B答案。没有良好思维习惯的学生是不能正确解答本题的。本题实际上就是判断四种情景下弹簧所受弹力的大小。由于弹簧的质量不计,所以不论弹簧做何种运动,弹簧各处的弹力大小都相等。因此这四种情况下弹簧的弹力是相等,即四个弹簧的伸长量是相等。只有D选项正确。
例4、某卫星沿椭圆轨道绕行星运行,近地点离行星中心的距离是a,远地点离行星中心的距离为b,若卫星在近地点的速率为Va,则卫星在远地点时的速率Vb多少?
错解:卫星运行所受的万有引力提供向心力,在近地点时,有![]() ,在远地点时有
,在远地点时有![]() ,上述两式相比得
,上述两式相比得![]() ,故
,故![]() 。
。
分析与解:以上错误在于认为做椭圆运动的卫星在近地点和远地点的轨道曲率半径不同。实际做椭圆运动的卫星在近地点和远地点的轨道曲率半径相同,设都等于R。所以,在近地点时有![]() ,在远地点时有
,在远地点时有![]() ,上述两式相比得
,上述两式相比得![]() ,故
,故![]() 。
。
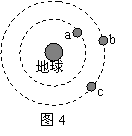 例5、如图4所示,a、b、c是在地球大气层外圆形轨道上运动的3颗卫星,下列说法正确的是:
例5、如图4所示,a、b、c是在地球大气层外圆形轨道上运动的3颗卫星,下列说法正确的是:
A.b、c的线速度大小相等,且大于a的线速度;
B.b、c的向心加速度大小相等,且大于a的向心加速度;
C.c加速可追上同一轨道上的b,b减速可等候同一轨道上的c;
D.a卫星由于某原因,轨道半径缓慢减小,其线速度将增大。
错解:c加速可追上b,错选C。
分析与解:因为b、c在同一轨道上运行,故其线速度大小、加速度大小
均相等。又b、c轨道半径大于a的轨道半径,由![]() 知,Vb=Vc<Va,故A选项错;由加速度a=GM/r2可知ab=ac<aa,故B选项错。
知,Vb=Vc<Va,故A选项错;由加速度a=GM/r2可知ab=ac<aa,故B选项错。
当c加速时,c受到的万有引力F<mv2/r,故它将偏离原轨道做离心运动;当b减速时,b受到的万有引力F>mv2/r,
故它将偏离原轨道做向心运动。所以无论如何c也追不上b,b也等不到c,故C选项错。对这一选项,不能用![]() 来分析b、c轨道半径的变化情况。
来分析b、c轨道半径的变化情况。
对a卫星,当它的轨道半径缓慢减小时,在转动一段较短时间内,可近似认为它的轨道半径未变,视为稳定运行,由![]() 知,r减小时V逐渐增大,故D选项正确。
知,r减小时V逐渐增大,故D选项正确。
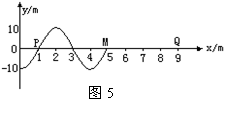 例6、 如图5所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )
例6、 如图5所示,一列简谐横波沿x轴正方向传播,从波传到x=5m的M点时开始计时,已知P点相继出现两个波峰的时间间隔为0.4s,下面说法中正确的是( )
A.这列波的波长是4m
B.这列波的传播速度是10m/s
C.质点Q(x=9m)经过0.5s才第一次到达波峰
D.M点以后各质点开始振动时的方向都是向下
错解:由质点Q(x=9m),经过0.4s波传到它,又经过T/4(0.1s)Q点第一次到达波峰,所以C对。
分析与解:(1)从图5上可以看出波长为4m,选A。
(2)实际上“相继出现两个波峰”应理解为,出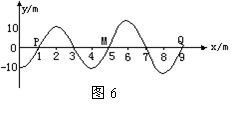 现第一波峰与出现第二个波峰之间的时间间隔。因为在一个周期内,质点完成一次全振动,而一次全振动应表现为“相继出现两个波峰”,即T=0.4s。则V=λ/T=10m/s,所以B选项正确。
现第一波峰与出现第二个波峰之间的时间间隔。因为在一个周期内,质点完成一次全振动,而一次全振动应表现为“相继出现两个波峰”,即T=0.4s。则V=λ/T=10m/s,所以B选项正确。
(3)质点Q(x=9m)经过0.4s开始振动,而波是沿x轴正方向传播,即介质中的每一个质点都被它左侧的质点所带动,从波向前传播的波形图6可以看出,0.4s波传到Q时,其左侧质点在它下方,所以Q点在0.5s时处于波谷。再经过0.2ss即总共经过0.7s才第一次到达波峰,所以选项C错了。
(4)从波的向前传播原理可以知道,M以后的每个质点都是先向下振动的。所以选项D是对的。此题正确答案为A,B,D。
例7、蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目。一个质量为60kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处。已知运动员与网接触的时间为1.2s。若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小。(g=10m/s2)
错解:将运动员看质量为m的质点,从h1高处下落,刚接触网时速度的大小 ![]() (向下), 弹跳后到达的高度为h2,刚离网时速度的大小
(向下), 弹跳后到达的高度为h2,刚离网时速度的大小 ![]() (向上) ,以
(向上) ,以![]() 表示接触时间, 接触过程中运动员受到向上的弹力F和向下的重力mg。
表示接触时间, 接触过程中运动员受到向上的弹力F和向下的重力mg。
由动量定理得:(F-mg)Δt= mV2-mV1,由以上各式解得,![]() , 代入数值得:
, 代入数值得: ![]() 。
。
分析与解:错误原因是忽视了动量定理的矢量性。由动量定理得:
(F-mg)Δt=mV2+mV1,由以上各式解得,![]() 。
。
代入数值得: ![]() 。
。
还有如下一种常见错误:
错解:将运动员看质量为m的质点,从h1高处下落,刚接触网时速度的大小 ![]() (向下), 弹跳后到达的高度为h2,刚离网时速度的大小
(向下), 弹跳后到达的高度为h2,刚离网时速度的大小 ![]() (向上) ,以
(向上) ,以![]() 表示接触时间,由动量定理得:FΔt=mV2+mV1,
由以上各式解得,
表示接触时间,由动量定理得:FΔt=mV2+mV1,
由以上各式解得,![]() , 代入数值得:
, 代入数值得: ![]() 。
。
分析与解:错误原因是受力分析时掉重力。
 例8、如图7所示,一摆长为L的摆,摆球质量为m,带电量为-q,如果在悬点A放一正电荷q,要使摆球能在竖直平面内做完整的圆周运动,则摆球在最低点的速度最小值应为多少?
例8、如图7所示,一摆长为L的摆,摆球质量为m,带电量为-q,如果在悬点A放一正电荷q,要使摆球能在竖直平面内做完整的圆周运动,则摆球在最低点的速度最小值应为多少?
错解:摆球运动到最高点时,最小速度为![]() ,由于摆在运动过程中,只有重力做功,故机械能守恒。据机械能守恒定律得:
,由于摆在运动过程中,只有重力做功,故机械能守恒。据机械能守恒定律得:
![]() 解得:
解得:![]() 。
。
分析与解:摆球运动到最高点时,受到重力mg、库仑力![]() 、绳的拉力T作用,根据向心力公式可得:
、绳的拉力T作用,根据向心力公式可得:![]() ,由于
,由于![]() ,所以有:
,所以有:
![]()
由于摆在运动过程中,只有重力做功,故机械能守恒。据机械能守恒定律得:
![]()
解得:![]() 。
。
例9、下列是一些说法:
①一质点受两个力作用且处于平衡状态(静止或匀速),这两个力在同一段时间内的冲量一定相同;
②一质点受两个力作用且处于平衡状态(静止或匀速),这两个力在同一段时间内做的功或者都为零,或者大小相等符号相反;
③在同样的时间内,作用力和反作用力的功大小不一定相等,但正负号一定相反;
④在同样的时间内,作用力和反作用力的功大小不一定相等,但正负号也不一定相反;
以上说法正确的是
A.①② B.①③② C.②③ D.②④
错解:认为“在同样的时间内,作用力和反作用力的功大小不一定相等,但正负号一定相反”而错选B。
分析与解:说法1不正确,因为处于平衡状态时,两个力大小相等方向相反,在同一段时间内冲量大小相等,但方向相反。由恒力做功的知识可知,说法2正确。关于作用力和反作用力的功要认识到它们是作用在两个物体上,两个物体的位移可能不同,所以功可能不同,说法3不正确,说法4正确。正确选项是D。
 例10、一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的。今把质点从O点的正上方离O点的距离为
例10、一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的。今把质点从O点的正上方离O点的距离为![]() 的O1点以水平的速度
的O1点以水平的速度![]() 抛出,如图8所示。试求;
抛出,如图8所示。试求;
(1)轻绳即将伸直时,绳与竖直方向的夹角为多少?
(2)当质点到达O点的正下方时,绳对质点的拉力为多大?
错解:很多同学在求解这道题时,对全过程进行整体思维,设质点到达O点的正下方时速度为V,根据能量守恒定律可得:
![]()
根据向心力公式得:![]() ,解得:
,解得:![]() .
.
 分析与解:上述解法是错误的。这些同学对物理过程没有弄清楚,忽视了在绳被拉直瞬时过程中机械能的瞬时损失。其实质点的运动可分为三个过程:
分析与解:上述解法是错误的。这些同学对物理过程没有弄清楚,忽视了在绳被拉直瞬时过程中机械能的瞬时损失。其实质点的运动可分为三个过程:
第一过程:质点做平抛运动。设绳即将伸直时,绳与竖直方向的夹角为![]() ,如图30所示,则
,如图30所示,则![]() ,
,
![]() ,其中
,其中![]()
联立解得![]() 。
。
第二过程:绳绷直过程。绳棚直时,绳刚好水平,如图9所示.由于绳不可伸长,故绳绷直时,V0损失,质点仅有速度V⊥,且![]() 。
。
第三过程:小球在竖直平面内做圆周运动。设质点到达O点正下方时,速度为V′,根据机械能守恒守律有:
![]()
设此时绳对质点的拉力为T,则![]() ,联立解得:
,联立解得:![]()