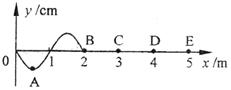高三年级物理综合测试试题
(120分钟 满分150分钟)
第Ⅰ卷(60分)
|
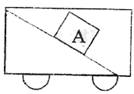
1.如图所示,小车内有一光滑斜面,当小车在水平轨道上
做匀变速直线运动时,小物块A恰好能与斜面保持相
对静止,在小车运动过程中的某时刻(此时小车速度
不为零),突然使小车迅速停止,则小车迅速停止的过
程中,小物块A可能 ( )
A.沿斜面滑下
B.沿斜面向上滑
C.仍与斜面保持相对静止
D.离开斜面做曲线运动
2.一石块从高度为H处自由下落,当速度达到落地速度的一半时,它下落的距离等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.汽车以额定功率行驶时,可能做下列哪些运动 ( )
A.匀速直线运动 B.匀加速直线运动
C.减速直线运动 D.匀速圆周运动
|
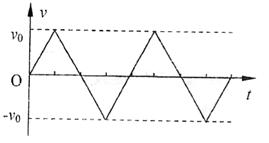
此物体 ( )
A.在做往复运动
B.在做加速大小不变的运动
C.只朝一个方向运动
D.在做匀速运动
|
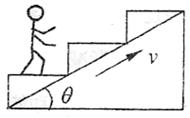
A.加速上升进程中![]() ,f、N、G都做功
,f、N、G都做功
B.加速上升过程中![]() ,N不做功
,N不做功
C.匀速过程中f=0,N、G都做功
|
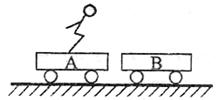
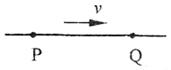
6.如图所示两辆质量相同的小车静止于光滑的水平面上,
有一人静止在小车A上。当这个人从A车上跳到B
车上,接着双从B车跳回并与A车保持相对静止时,
A车的速率 ( )
A.等于零 B.小于B车速率
C.大于B车速率 D.等于B车速率
7.质量为M的汽车在平直的公路上行驶,发动机的输出功率P和汽车所受的阻力f都恒定不变,在时间t内,汽车的速度由v0增加到最大速度vm,汽车前进的距离为s,则在这段时间内发动机所做的功可用下列哪些式子计算 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
A.1个 B.2个
C.3个 D.4个
|
波传播到x轴上的B质点,在它左边的A质点正
在负最大位移处,如图所示,在t=0.6s时,质点A
第二次出现在正的最大位移处,则 ( )
A.该简谐波的波速等于10m/s
B.t = 0.6s时,质点C在平衡位置处且向上运动
C.t = 0.6s时,质点C在平衡位置处且向下运动
D.当质点E第一次出现在正最大位移处时,质点B恰好在平衡位置且向下运动
|
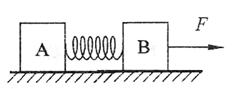
A.系统的总动量不断减少
B.弹簧恢复原长时,系统动能最大
C.弹簧压缩到最短时,两物体速度相等
D.弹簧压缩到最短时,系统动能最小
|
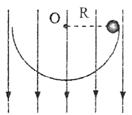
A.小球在运动过程中机械能守恒
B.小球经过环的最低点时速度最大
C.小球经过环的最低点时对轨道压力为![]()
|
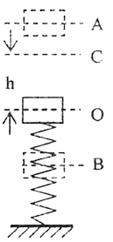
12.如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,
在竖直方向的A、B两点间做简谐运动,O为平衡位置,
振子的振动周期为T,某一时刻物体正经过C点向上运
动(C点在平衡位置上方h高处),从此时刻开始的半
个周期内 ( )
A.重力对物体做功2mgh
B.重力对物体的冲量大小为mgT/2
C.振子的加速度方向始终不变
|
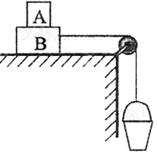
13.物块A、B叠放在水平面上,装砂的铁桶C通过细线牵
引A、B在水平面上向右匀加速运动,设A、B间的摩
擦力为f1,B与桌面间的摩擦力为f2,若增大C桶内砂
的质量,而A、B仍一起向右运动,则摩擦力f1和f2的
变化情况是 ( )
A.f1不变,f2变大 B.f1变大,f2不变
C.f1和f2都变大 D.f1和f2都不变
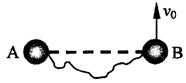
14.质量相等的两小球A、B由不可伸长的细绳相连放在光滑
水平面上,绳处于松驰状态,现给B一个垂直AB连线的水
|
A.AB组成的系统动量守恒
B.AB组成的系统沿绳方向动量守恒
C.AB组成的系统机械能守恒
D.AB组成的系统机械能不守恒
15.同步卫星的质量为M,离地面的高度为h,R表示地球的半径,g表示地球表面的重力加速度,ω表示地球自转的角速度,则卫星所受到地球对它的万有引力的大小为( )
A.0 B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(共90分)
|
16.(20分)在用打点计时器验证机械能守恒
定律的实验中,质量m=1.00kg的重物自
由下落,打点计时器在纸带上打出一系列
点。如图所示为选取的一条符合实验要求
的纸带,O为第一个点,A、B、C为从合
适位置开始选取的三个连续点(其他点未
画出)。
已知打点计时器每隔0.02s打一次点,当地的重力加速度g=9.80m/s2。那么:
(1)纸带的 端(选填“左”或“右”)与重物相连;
(2)根据图上所得的数据,应取图中O点和 点来验证机械能守恒定律;
|
(4)实验的结论是 。
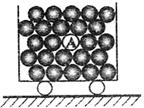
17.(5分)如图所示,有一辆汽车载满西瓜在水平路面上匀速
前进,突然发现意外情况紧急刹车做匀减运动,加速度大
小为a,设中间有一质量为m的西瓜A,则A受其他西瓜
对它作用力的大小为 。
|
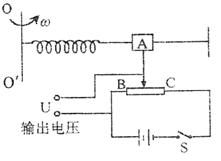
的转动角速度,其结构如下图所示。当系统
绕OO′转动时,元件A发生位移并输出电
压信号,成为飞机、卫星等的制导系统的信
息源。已知A的质量为m,弹簧的劲度系数
为k,自然长度为L,电源的电动势为E,
电源内阻不计,滑动变阻器的总长度也为L,
电阻分布均匀,系统静止时滑动变阻器的滑动触
片在B点,此时弹簧在原长处。闭合电
源开关,当系统以角速度ω转动时,输出电压U和ω的函数关系为 。
|
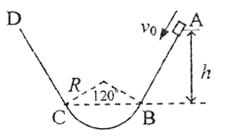
20.(14分)如图所示,AB和CD为两个对称斜面,两斜面足够长,斜面的下端分别与一个光滑的圆弧面的两端相切,圆弧圆心角为120°,半径R=2.0m,一个质量为m=1kg的物体在离圆弧BC连线高度为h=3.0m处以初速度v0=4.0m/s沿斜面运动,若物体与斜面间的动摩擦因数μ=0.2,重力加速度g=10m/s2。则
(1)物体在斜面上(不包括圆弧部分)走过的路程的最大值为多大?
(2)试描述物体最终的运动情况。
(3)物体对圆弧最低点的最大压力和最小压力分别为多少?
|
|
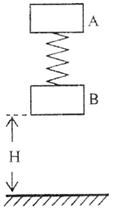
22.(16分)如图所示,将质量均为m厚度不计的两块物A、B用轻质弹簧相连接。第一次只用手托着B物块于H高度,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能为EP,现由静止释放A,B,B物块刚要落地前瞬间将弹簧瞬间解除锁定(解除锁定无机械能损失),B物块着地后速度立即变为0,在随后的过程中B物块恰能离开地面但不继续上升。第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0。求:
|
(2)第二次释放A、B后,B刚要离地时A的速度v2。
参考答案
一、选择题(4分,2分,0分)
1.BD 2.B 3.ACD 4.AB 5.AC 6.B 7.CD 8.D 9.B
10.BCD 11.BC 12.ABD 13.B 14.ABD 15.BCD
二、非选择题(共90分)
16.(1)左 (2)B (3)1.88、1.84
(4)在误差允许范围内重物下落过程中机械能守恒。(每空5分)
17.![]() (5分)
(5分)
18.![]() (5分)
(5分)
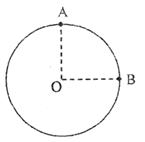
19.(14分)顺时针跑动时![]() (4分)
(4分)
![]() (3分)
(3分)
逆时针跑动时![]() (4分)
(4分)
![]() (3分)
(3分)
20.(14分)
(1)物体在两斜面上来回运动时,克服摩擦力做功![]() ①
①
物体从开始直到不再在斜面上运动过程中
![]() ② (3分)
② (3分)
解得:![]()
(2)物体最终是在BC之间的圆弧上来回做变带圆周运动,且在BC点时速度为零。(2分)
(3)物体第一次通过圆弧最低点时,圆弧所做受到的压力最大。
依动能定理![]() ① (2分)
① (2分)
依牛顿第二定律![]() ② 解得:
② 解得:![]() (2分)
(2分)
物体最终在圆弧上运动时,圆弧所受的压力最小
依动能定理![]() ③(2分)
③(2分)
依牛顿第二定律![]() ④ 解得:
④ 解得:![]() (2分)
(2分)
21.(16分)
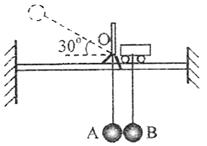
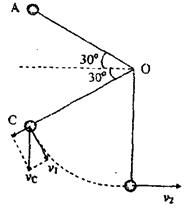
如图A球从静止释放持后自由落至C点悬线绷直,此时速度为vc
|
![]() (2分)
(2分)
在绷直的过程中沿线的速度分量减为零时,
A球将以切向速度v1沿圆弧运动,且
![]() (2分)
(2分)
A球从C点运动到最低点与B球碰撞前机械能守恒,
可求出A球和B球碰前的速度v2,即
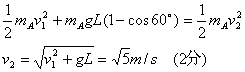
因AB两球发生无机械能损失的碰撞且![]() ,所以它们的速度交换,即碰后A球的速度为零,B球的速度为
,所以它们的速度交换,即碰后A球的速度为零,B球的速度为![]() ,对B球和小车组成的系统水平方向动量守恒和机械能守恒,当两者有共同速度μ,B球上升到最高点,设上升高度为h。
,对B球和小车组成的系统水平方向动量守恒和机械能守恒,当两者有共同速度μ,B球上升到最高点,设上升高度为h。
![]() (2分)
(2分)
![]() (2分)
(2分)
在B球回摆到最低点的过程中,悬线拉力会使小车加速,当B球回到最低点时,小车有最大速度vm,设此时B球回到最低点的速度大小为v3,根据动量守恒定律和机械能守恒定律有
![]() (2分)
(2分)
解得![]() (2分)
(2分)
22.(16分)
(1)第二次释放A、B后,A、B自由落体运动,B着地后,A和弹簧相互作用至A上升到弹簧恢复原长过程中,弹簧对A做的总功为零。(2分)
对A从开始下落至弹簧恢复原长过程,对A由动能定理有![]() ①(2分)
①(2分)
解得![]() 方向向上(1分)
方向向上(1分)
(2)设弹簧的劲度系数为k,第一次释放A、B前,弹簧向上弹力与A的重力平衡,且设弹簧形变量(压缩量)为![]() ② (1分)
② (1分)
第一次释放A、B后,B则刚要高地时弹簧产生向上的弹力与B的重力平衡,设弹簧的形变量(伸长量为)为![]() ③ (1分)
③ (1分)
第二次释放A、B后,B则刚要高地时弹簧产生向上的弹力与B的重力平衡,设弹簧的形变量(伸长量为)为![]() ④ (1分)
④ (1分)
由②③④得![]() ⑤
⑤
即三个状态的弹性势能都相等为EP (1分)
在第一次释放A、B后至B着地前过程,对A、B和弹簧组成的系统由机械能守恒有
![]() ⑥
(1分)
⑥
(1分)
从B着地后到B刚要高地的过程,对A和弹簧组成的系统由机械能守恒有
![]() ⑦
(3分)
⑦
(3分)
第二次释放,对A和弹簧组成的系统,从A上升至弹簧恢复原长到B刚要高地过程,由机械能守恒有![]() ⑧ (2分)
⑧ (2分)
由⑥⑦⑧得![]() (1分)
(1分)