高三物理电磁感应单元测试题 组题:于忠慈(2008)
一、选择题
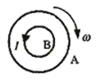 1、两圆环A、B置于同一水平面上,其中A为均匀带电绝缘环,B为导体环,当A以如图所示的方向绕中心转动的角速度发生变化时,B中产生如图所示方向的感应电流.则【
】
1、两圆环A、B置于同一水平面上,其中A为均匀带电绝缘环,B为导体环,当A以如图所示的方向绕中心转动的角速度发生变化时,B中产生如图所示方向的感应电流.则【
】
(A)A可能带正电且转速减小
(B)A可能带正电且转速增大
(C)A可能带负电且转速减小
(D)A可能带负电且转速增大
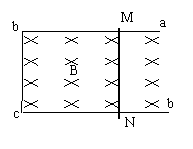 2、如图所示,abcd是光滑水平放置的U形金属框,MN为导体棒,静止在框架上,有一竖直向下的匀强磁场垂直穿过导轨平面,当匀强磁场的磁感应强度B发生变化时,关于MN导体棒的运动下列说法正确的是【
】
2、如图所示,abcd是光滑水平放置的U形金属框,MN为导体棒,静止在框架上,有一竖直向下的匀强磁场垂直穿过导轨平面,当匀强磁场的磁感应强度B发生变化时,关于MN导体棒的运动下列说法正确的是【
】
(A)当B增大时,MN棒向右运动;
(B)当B增大时,MN棒向左运动;
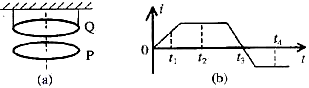 (C)当B减小时,MN棒向右运动;
(C)当B减小时,MN棒向右运动;
(D)当B减小时,MN棒向左运动。
3、如图(![]() ),圆形线圈P静止在水平桌面上,其正上方悬挂一相同的线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为N,则【
】
),圆形线圈P静止在水平桌面上,其正上方悬挂一相同的线圈Q,P和Q共轴,Q中通有变化电流,电流随时间变化的规律如图(b)所示,P所受的重力为G,桌面对P的支持力为N,则【
】
(A)![]() 时刻N>G。 (B)
时刻N>G。 (B)![]() 时刻N>G。
时刻N>G。
 (C)
(C)![]() 时刻N<G。 (D)
时刻N<G。 (D)![]() 时刻N=G。
时刻N=G。
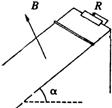
4、如图所示,有两根和水平方向成。角的光滑平行的金属轨道,上端接有可变电阻R,下端足够长,空间有垂直于轨道平面的匀强磁场,磁感强度为及一根质量为m的金属杆从轨道上由静止滑下。经过足够长的时间后,金属杆的速度会趋近于一个最大速度几,则【 】
(A)如果B增大,vm将变大
(B)如果α变大,vm将变大
(C)如果R变大,vm将变大
(D)如果m变小,vm将变大
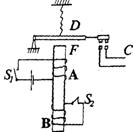 5、如图所示是一种延时开关,当S1闭合时,电磁铁F将衔铁D吸下,C线路接通。当S1断开时,由于电磁感应作用,D将延迟一段时间才被释放。则【 】
5、如图所示是一种延时开关,当S1闭合时,电磁铁F将衔铁D吸下,C线路接通。当S1断开时,由于电磁感应作用,D将延迟一段时间才被释放。则【 】
(A)由于A线圈的电磁感应作用,才产生延时释放D的作用
(B)由于B线圈的电磁感应作用,才产生延时释放D的作用
(C)如果断开B线圈的电键S2,无延时作用
(D)如果断开B线圈的电键S2,延时将变长
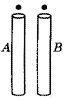 6、如图所示,A、B为大小、形状均相同且内壁光滑,但用不同材料制成的圆管,竖直固定在相同高度.两个相同的磁性小球,同时从A、B管上端的管口无初速释放,穿过A管的小球比穿过B管的小球先落到地面.下面对于两管的描述中可能正确的是【
】
6、如图所示,A、B为大小、形状均相同且内壁光滑,但用不同材料制成的圆管,竖直固定在相同高度.两个相同的磁性小球,同时从A、B管上端的管口无初速释放,穿过A管的小球比穿过B管的小球先落到地面.下面对于两管的描述中可能正确的是【
】
(A)A管是用塑料制成的,B管是用铜制成的
(B)A管是用铝制成的,B管是用胶木制成的
(C)A管是用胶木制成的,B管是用塑料制成的
(D)A管是用胶木制成的,B管是用铝制成的
7、.粗细均匀的电阻丝围成的正方形线框置于有界匀强磁场中,磁场方向垂直于线框平面,其边界与正方形线框的边平行。现使线框以同样大小的速度沿四个不同方向平移出磁场,如图所示,则在移出过程中线框一边a、b两点间的电势差绝对值最大的是【
】
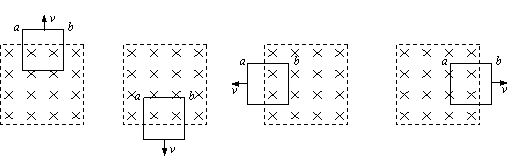

A. B. C. D.
8、如图所示,A是长直密绕通电螺线管.小线圈B与电流表连接,并沿A的轴线OX从D点自左向右匀速穿过螺线管A.能正确反映通过电流表中电流,随工变化规律的是【
】
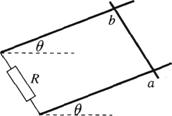
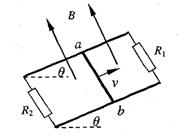 9、如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿导轨向上滑动,当上滑的速度为V时,受到安培力的大小为F.此时【
】
9、如图所示,平行金属导轨与水平面成θ角,导轨与固定电阻R1和R2相连,匀强磁场垂直穿过导轨平面.有一导体棒ab,质量为m,导体棒的电阻与固定电阻R1和R2的阻值均相等,与导轨之间的动摩擦因数为μ,导体棒ab沿导轨向上滑动,当上滑的速度为V时,受到安培力的大小为F.此时【
】
(A)电阻R1消耗的热功率为Fv/3.
(B)电阻 R1消耗的热功率为 Fv/6.
(C)整个装置因摩擦而消耗的热功率为μmgvcosθ.
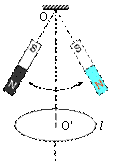 (D)整个装置消耗的机械功率为(F+μmgcosθ)
(D)整个装置消耗的机械功率为(F+μmgcosθ)
10、如图,一条形磁铁用线悬挂于0点,在O点的正下方固定放置一水平的金属圆环l。现使磁铁沿竖直平面来回摆动,则【 】
(A)在一个周期内,圆环中感应电流方向改变二次。
(B)磁铁始终受到感应电流磁场的斥力作用。
(C)磁铁所受感应电流磁场的作用力有时是阻力,有时是动力。
(D)磁铁所受感应电流磁场的作用力始终是阻力。
二、填空题
11、已知某一区域的地下埋有一根与地表面平行的直线电缆,电缆中通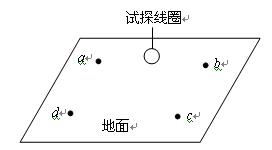 有变化的电流,在其周围有变化的磁场,因此可以通过在地面上测量闭合试探小线圈中的感应电动势来探测电缆的确切位置、走向和深度.当线圈平面平行地面测量时,在地面上a、c两处测得试探线圈中的电动势为零,b、d两处线圈中的电动势不为零;当线圈平面与地面成45°夹角时,在b、d两处测得试探线圈中的电动势为零.经过测量发现,a、b、c、d恰好位于边长为1m的正方形的四个顶角上,如图所示.据此可以判定地下电缆在___________两点连线的正下方,离地表面的深度为___________m.
有变化的电流,在其周围有变化的磁场,因此可以通过在地面上测量闭合试探小线圈中的感应电动势来探测电缆的确切位置、走向和深度.当线圈平面平行地面测量时,在地面上a、c两处测得试探线圈中的电动势为零,b、d两处线圈中的电动势不为零;当线圈平面与地面成45°夹角时,在b、d两处测得试探线圈中的电动势为零.经过测量发现,a、b、c、d恰好位于边长为1m的正方形的四个顶角上,如图所示.据此可以判定地下电缆在___________两点连线的正下方,离地表面的深度为___________m.
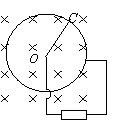 12、图示装置,半径为r的圆形导体框架放在磁感应强度为B的匀强磁场中,导体棒OC可绕圆心O在框架上转动,棒端O与框架连接电阻R(其它电阻不计)。在外力作用下,棒以角速度w 匀角速转动,则通过电阻的电流为___________;外力的功率为__________。
12、图示装置,半径为r的圆形导体框架放在磁感应强度为B的匀强磁场中,导体棒OC可绕圆心O在框架上转动,棒端O与框架连接电阻R(其它电阻不计)。在外力作用下,棒以角速度w 匀角速转动,则通过电阻的电流为___________;外力的功率为__________。
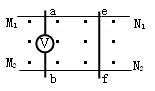 13、如图所示,M1N1与M2N2是位于同一水平面内的两条平行金属导轨,导轨间的距离为L。磁感强度为B的匀强磁场与导轨所在平面相垂直。ab与ef为两根金属杆,与导轨垂直并可在导轨上滑动,其中金属杆ab上串有一电压表。除电压表外其它电阻均不计,当保持ab杆不动,让ef杆以速度v向右滑动时,电压表的读数为________;当两杆一起以速度v向右滑动时,电压表的读数为________。
13、如图所示,M1N1与M2N2是位于同一水平面内的两条平行金属导轨,导轨间的距离为L。磁感强度为B的匀强磁场与导轨所在平面相垂直。ab与ef为两根金属杆,与导轨垂直并可在导轨上滑动,其中金属杆ab上串有一电压表。除电压表外其它电阻均不计,当保持ab杆不动,让ef杆以速度v向右滑动时,电压表的读数为________;当两杆一起以速度v向右滑动时,电压表的读数为________。
 14、物理学家法拉第在研究电磁学时,亲手做过许多实验。如图所示的实验就是著名的电磁旋转实验,这种现象是:如果载流导线附近只有磁铁的一个极,磁铁就会围绕导线旋转;反之,载流导线也会围绕单独的某一磁极旋转。这一装置实际上就成为最早的电动机。图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁。图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上。请你判断这时自上向下看,A将________转动和C将________转动(填顺时针还是逆时针)。
14、物理学家法拉第在研究电磁学时,亲手做过许多实验。如图所示的实验就是著名的电磁旋转实验,这种现象是:如果载流导线附近只有磁铁的一个极,磁铁就会围绕导线旋转;反之,载流导线也会围绕单独的某一磁极旋转。这一装置实际上就成为最早的电动机。图中A是可动磁铁,B是固定导线,C是可动导线,D是固定磁铁。图中黑色部分表示汞(磁铁和导线的下半部分都浸没在汞中),下部接在电源上。请你判断这时自上向下看,A将________转动和C将________转动(填顺时针还是逆时针)。
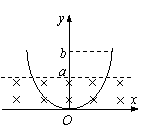 15、如图所示,以一竖直光滑曲面的顶点为坐标原点,建立坐
15、如图所示,以一竖直光滑曲面的顶点为坐标原点,建立坐
标系。曲面的下半部分处在一匀强磁场中,磁场方向垂直曲面所在平面指向纸内,磁场的上边界是y=a的直线。一个质量为m的小金属块从曲面上y=b(b>a)处以初速度v0沿曲面下滑,则金属块第一次到达磁场上边界时的速度大小为____;金属块在曲面上滑动的过程中产生的总热量为__________。
三、实验题
16、如图所示器材可用来研究电磁感应现象及判定感应电流方向.
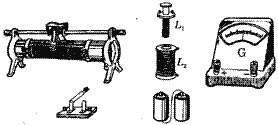
(1)在给出的实物图中,用实线作为导线将实验器材连成实验电路.
(2)将线圈L1插入L2中,合上开关.能使感应电流与原电流的绕行方向相同的实验操作是___________. A.插入软铁棒 B.拔出线圈L1
C.使变阻器阻值变大 D.断开开关
17、在研究电磁感应现象实验中,
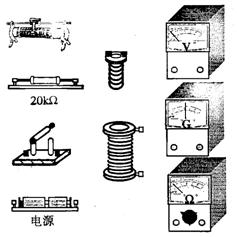
(1)为了能明显地观察到实验现象,请在如图所示的实验器材中,选择必要的器材,在图中用实线连接成相应的实物电路图;
(2)将原线圈插人副线圈中,闭合电键,副线圈中感生电流与原线圈中电流的绕行方向 (填“相同”或“相反”);
(3)将原线圈拔出时,副线圈中的感生电流与 原线圈中电流的绕行方向 (填“相同”或“相反”).
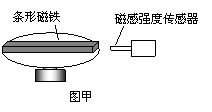 18、某同学在实验室里熟悉各种仪器的使用。他将一条形磁铁放在转盘上,如图甲所示,磁铁可随转盘转动,另将一磁感强度传感器固定在转盘旁边,当转盘(及磁铁)转动时,引起磁感强度测量值周期性地变化,该变化与转盘转动的周期一致。经过操作,该同学在计算机上得到了如图乙所示的图像[ ]
18、某同学在实验室里熟悉各种仪器的使用。他将一条形磁铁放在转盘上,如图甲所示,磁铁可随转盘转动,另将一磁感强度传感器固定在转盘旁边,当转盘(及磁铁)转动时,引起磁感强度测量值周期性地变化,该变化与转盘转动的周期一致。经过操作,该同学在计算机上得到了如图乙所示的图像[ ]
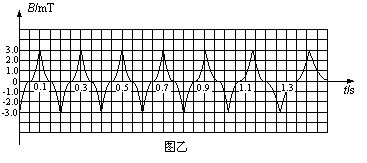

(1)在图像记录的这段时间内,圆盘转动的快慢情况是___________________。
(2)圆盘匀速转动时的周期是___________________s。
(3)该同学猜测磁感强度传感器内有一线圈,当测得磁感强度最大时就是穿过线圈的磁通量最大时。按照这种猜测[ ]
(A)在t = 0.1s 时刻,线圈内产生的感应电流的方向发生了变化。
(B)在t = 0.15s 时刻,线圈内产生的感应电流的方向发生了变化。
(C)在t = 0.1s 时刻,线圈内产生的感应电流的大小达到了最大值。
(D)在t = 0.15s 时刻,线圈内产生的感应电流的大小达到了最大值。
四、计算题
 19、如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距lm,导轨平面与水平面成θ=37°角,下端连接阻值为尺的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计
19、如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距lm,导轨平面与水平面成θ=37°角,下端连接阻值为尺的电阻.匀强磁场方向与导轨平面垂直.质量为0.2kg、电阻不计
的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻尺消耗的功率为8W,求该速度的大小;
(3)在上问中,若R=2Ω,金属棒中的电流方向由a到b,求磁感应强度的大小与方向.
(g=10rn/s2,sin37°=0.6, cos37°=0.8)
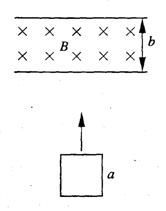 20、如图所示,将边长为a、质量为m、电阻为R的正方形导线框竖直向上抛出,穿过宽度为b、磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.线框向上离开磁场时的速度刚好是进人磁场时速度的一半,线框离开磁场后继续上升一段高度,然后落下并匀速进人磁场.整个运动过程中始终存在着大小恒定的空气阻力f且线框不发生转动.求:
20、如图所示,将边长为a、质量为m、电阻为R的正方形导线框竖直向上抛出,穿过宽度为b、磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.线框向上离开磁场时的速度刚好是进人磁场时速度的一半,线框离开磁场后继续上升一段高度,然后落下并匀速进人磁场.整个运动过程中始终存在着大小恒定的空气阻力f且线框不发生转动.求:
(1)线框在下落阶段匀速进人磁场时的速度V2;
( 2)线框在上升阶段刚离开磁场时的速度V1;
(3)线框在上升阶段通过磁场过程中产生的焦耳热Q.
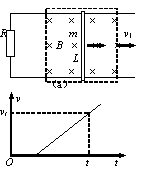 21、如图(a)所示,光滑的平行长直金属导轨置于水平面内,间
21、如图(a)所示,光滑的平行长直金属导轨置于水平面内,间
距为L、导轨左端接有阻值为R的电阻,质量为m的导体棒垂直跨接在导轨上。导轨和导体棒的电阻均不计,且接触良好。在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场,磁感应强度大小为B。开始时,导体棒静止于磁场区域的右端,当磁场以速度v1匀速向右移动时,导体棒随之开始运动,同时受到水平向左、大小为f的恒定阻力,并很快达到恒定速度,此时导体棒仍处于磁场区域内。
(1)求导体棒所达到的恒定速度v2;
(2)为使导体棒能随磁场运动,阻力最大不能超过多少?
(3)导体棒以恒定速度运动时,单位时间内克服阻力所做的功和电路中消耗的电功率各为多大?
(4)若t=0时磁场由静止开始水平向右做匀加速直线运动,经过较短时间后,导体棒也做匀加速直线运动,其v-t关系如图(b)所示,已知在时刻t导体棋睥瞬时速度大小为vt,求导体棒做匀加速直线运动时的加速度大小。
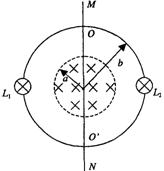 22、半径为a的圆形区域内有均匀磁场,磁感强度为B=0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a=0.4m,b=0.6m,金属环上分别接有灯L1、L2,两灯的电阻均为R0=2Ω,一金属棒MN与金属环接触良好,棒与环的电阻均忽略不计
22、半径为a的圆形区域内有均匀磁场,磁感强度为B=0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a=0.4m,b=0.6m,金属环上分别接有灯L1、L2,两灯的电阻均为R0=2Ω,一金属棒MN与金属环接触良好,棒与环的电阻均忽略不计
(1)若棒以v0=5m/s的速率在环上向右匀速滑动,求棒滑过圆环直径OO’的瞬时(如图所示)MN中的电动势和流过灯L1的电流。
(2)撤去中间的金属棒MN将右面的半圆环OL2O’以OO’为轴向上翻转90º,若此时磁场随时间均匀变化,其变化率为ΔB/Δt=(4 /Ω)T/s,求L1的功率。
参考答案
一、 选择题
1、 BC
2、 BC
3、 AD
4、 BC
5、 BC
6、 AD
7、 B
8、 C
9、 BCD
10、 D
二、 填空题
11、ac 0.71
12、,
13、BLV;0
14、逆时针,顺时针
15、,mg(b-a)+mv02/2,
三、实验题
16、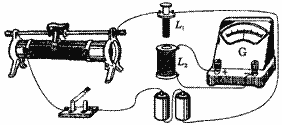 BCD
BCD
17、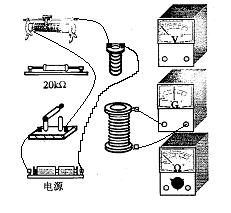 (1)如图(2)相反(3)相同
(1)如图(2)相反(3)相同
18、(1)先快慢不变,后越来越慢(2分)(2)0.2 (2分)(3)A C (2分)
四、计算题
19、解:(1)金属棒开始下滑的初速为零,根据牛顿第二定律
mgsinθ-μmgcosθ=ma ①
由①式解得a=10×(O.6-0.25×0.8)m/s2=4m/s2 ②
(2夕设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡
mgsinθ一μmgcos0一F=0 ③
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率
Fv=P ④
由③、④两式解得![]() ⑤
⑤
(3)设电路中电流为I,两导轨间金属棒的长为l,磁场的磁感应强度为B
![]() ⑥
⑥
P=I2R ⑦
由⑥、⑦两式解得![]() ⑧
⑧
磁场方向垂直导轨平面向上
20、解:(1)因为线框在下落阶段匀速进人磁场则:
![]()
(2)离开磁场上升阶段:![]()
下降阶段:![]()
联立两式可得 ![]()
(3)线框在上升阶段通过磁场过程中产生的焦耳热Q,则由题意知:
![]()
解得![]()
21、解:(1)E=BL(v1-v2),I=E/R,F=BIL=,速度恒定时有:
=f,可得:v2=v1-,
(2)fm=,
(3)P导体棒=Fv2=f,P电路=E2/R==,
(4)因为-f=ma,导体棒要做匀加速运动,必有v1-v2为常数,设为Dv,a=,则-f=ma,可解得:a=。

22、解:(1)ε1=B2av=0.2×0.8×5=0.8V ①
I1=ε1/R=0.8/2=0.4A ②
(2)ε2=ΔФ/Δt=0.5×πa2×ΔB/Δt=0.32V ③
P1=(ε2/2)2/R=1.28×102W ④