高三物理复习测试试卷
李丹 08.2.29
第Ⅰ卷(选择题 共48分)
一、选择题.本题共12小题,每小题4分,共计48分.
 1.一带电粒子射入一正点电荷的电场中,运动轨迹如图所示,粒子从A运动到B,则下列说法中正确的是
1.一带电粒子射入一正点电荷的电场中,运动轨迹如图所示,粒子从A运动到B,则下列说法中正确的是
A.粒子带正电
 B.粒子的动能一直变大
B.粒子的动能一直变大
C.粒子的加速度先变小后变大
D.粒子在电场中的电势能先变小后变大
2.如图所示,小车上固定着三角硬杆,杆的端点固定着一个质量为m的小球.当小车水平向右的加速度逐渐增大时,杆对小球的作用力的变化(用F1至F4变化表示)可能是下图中的(OO'沿杆方向)
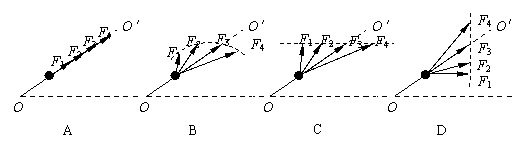 |
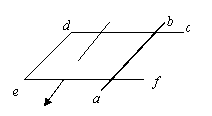
3.如图所示,金属棒ab置于水平放置的光滑框架cdef上,棒与框架接触良好,匀强磁场垂直于ab棒斜向下.从某时刻开始磁感应强度均匀减小,同时施加一个水平外力F使金属棒ab保持静止,则F
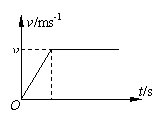 A.方向向右,且为恒力 B.方向向右,且为变力
A.方向向右,且为恒力 B.方向向右,且为变力
C.方向向左,且为变力 D.方向向左,且为恒力
4.一物体在粗糙的水平面上受到水平拉力作用,在一段时间内的速度随时间变化情况如右图所示.则拉力的功率随时间变化的图象是下图中的(g取10m/s2)
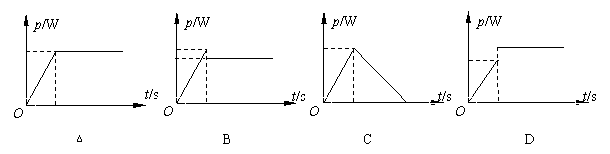
 5. 如图所示为用热敏电阻R和继电器L等组成的一个简单的恒温控制电路,其中热敏电阻的阻值会随温度的升高而减小.电源甲与继电器、热敏电阻等组成控制电路,电源乙与恒温箱加热器(图中未画出)相连接.则
5. 如图所示为用热敏电阻R和继电器L等组成的一个简单的恒温控制电路,其中热敏电阻的阻值会随温度的升高而减小.电源甲与继电器、热敏电阻等组成控制电路,电源乙与恒温箱加热器(图中未画出)相连接.则
A.当温度降低到某一数值,衔铁P将会被吸下
B.当温度升高到某一数值,衔铁P将会被吸下
C.工作时,应该把恒温箱内的加热器接在C、D端
D.工作时,应该把恒温箱内的加热器接在A、B端
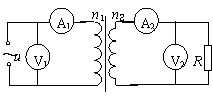 6.如图所示,一理想变压器原副线圈匝数之比为5∶1,原线圈端输入交流电压u=311sin100πt V,电阻R=44Ω,电流表和电压表对电路的影响忽略不计.下列说法中正确的是
6.如图所示,一理想变压器原副线圈匝数之比为5∶1,原线圈端输入交流电压u=311sin100πt V,电阻R=44Ω,电流表和电压表对电路的影响忽略不计.下列说法中正确的是
A.电压表V1的示数约为311V
B.电流表A1的示数约为0.20A
C.电压表V2的示数约为44V
D.电流表A2的示数约为1.4A
7.如图所示,光滑半球的半径为R,球心为O,其上方有一个光滑曲面轨道AB,高度为R/2.轨道底端水平并与半球顶端相切.质量为m的小球由A点静止滑下.小球在水平面上的落点为C,则
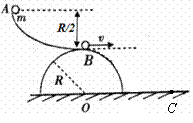 A.小球将沿半球表面做一段圆周运动后抛至C点
A.小球将沿半球表面做一段圆周运动后抛至C点
B.小球将从B点开始做平抛运动到达C点
C.OC之间的距离为![]()
D.OC之间的距离为R
8.土星的卫星众多,其中土卫五和土卫六的半径之比为![]() ,质量之比为
,质量之比为![]() ,围绕土星作圆周运动的半径之比为
,围绕土星作圆周运动的半径之比为![]() ,下列判断正确的是
,下列判断正确的是
A.土卫五和土卫六的公转周期之比为![]()
C.土星对土卫五和土卫六的万有引力之比为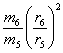
D.土卫五和土卫六表面的重力加速度之比为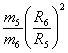
 B.土卫五和土卫六的公转速度之比为
B.土卫五和土卫六的公转速度之比为![]()
9.如图所示,一个滑雪运动员从左侧斜坡距离坡底8m处自由滑下,当下滑到距离坡底s1处时,动能和势能相等(以坡底为参考平面);到坡底后运动员又靠惯性冲上斜坡(不计经过坡底时的机械能损失),当上滑到距离坡底s2处时,运动员的动能和势能又相等,上滑的最大距离为4m.关于这个过程,下列说法中正确的是
A.摩擦力对运动员所做的功等于运动员动能的变化
B.重力和摩擦力对运动员所做的总功等于运动员动能的变化
C.s1<4m,s2>2m
D.s1>4m,s2<2m
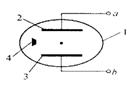 10.如图所示为用于火灾报警的离子式烟雾传感器原理图,在网 罩l内有电极板2和3,a、b端接电源,4是一小块放射性同位素镅241,它能放射出一种很容易使气体电离的粒子。平时镅放射出来的粒子使两个电极间的空气电离,形成较强的电流;发生火灾时,烟雾进入网罩内,烟的颗粒吸收空气中的离子和镅放射出来的粒子,导致电流变化,报警器检测出这种变化,发出报警。有关这种报警器的下列说法正确的是
10.如图所示为用于火灾报警的离子式烟雾传感器原理图,在网 罩l内有电极板2和3,a、b端接电源,4是一小块放射性同位素镅241,它能放射出一种很容易使气体电离的粒子。平时镅放射出来的粒子使两个电极间的空气电离,形成较强的电流;发生火灾时,烟雾进入网罩内,烟的颗粒吸收空气中的离子和镅放射出来的粒子,导致电流变化,报警器检测出这种变化,发出报警。有关这种报警器的下列说法正确的是
A.镅放射出来的是α粒子
B.镅放射出来的是β粒子
C.有烟雾时电流减弱
D.有烟雾时电流增强
11.下列说法中正确的是 ( BC )
A.一群氢原子处于n=3的激发态向较低能级跃迁,最多可放出二种频率的光子
B.由于每种原子都有自己的特征谱线,故可以根据原子光谱来鉴别物质
C.某原子核经过一次α衰变和两次β衰变后,核内中子数减少4个
D.中子和质子结合成氘核时吸收能量
 12.如图所示,一水平导轨处于与水平方向成45°角向左上方的匀强磁场中,一根通有恒定电流的金属棒,由于受到安培力作用而在粗糙的导轨上向右做匀速运动。现将磁场方向沿顺时针缓慢转动至竖直向上,在此过程中,金属棒始终保持匀速运动,已知棒与导轨间动摩擦因数μ<1,则磁感应强度B的大小变化情况是
12.如图所示,一水平导轨处于与水平方向成45°角向左上方的匀强磁场中,一根通有恒定电流的金属棒,由于受到安培力作用而在粗糙的导轨上向右做匀速运动。现将磁场方向沿顺时针缓慢转动至竖直向上,在此过程中,金属棒始终保持匀速运动,已知棒与导轨间动摩擦因数μ<1,则磁感应强度B的大小变化情况是
A.不变 B.一直增大
C.一直减小 D.先变小后变大
第Ⅱ卷(共102分)
二. 选作题(11 分)
13.(1) (4分)理论联系实际是物理学科特点之一。以下给出的几组表述中,实际应用与相应的物理理论相符合的是 ( )
①干涉法检查平面的平整度应用了光双缝干涉原理
②伦琴射线管应用了光电效应原理
③光纤通信应用了光的折射原理
④光谱分析应用了原子光谱理论
⑤立体电影应用了光的偏振理论
A.①② B.②③ C.③④ D.④⑤
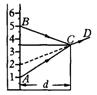 (2)(3分)如图所示,将刻度尺直立在装满某种透明液体的宽口瓶中(液体未漏出),从刻度尺上A、B两点射出的光线AC和BC在C点被折射和反射后都沿直线CD传播,已知刻度尺上相邻两根长刻度线间的距离为1 cm,刻度尺右边缘与宽口瓶右内壁间的距离d=2.5 cm,由此可知,瓶内液体的折射率n= (可保留根号).
(2)(3分)如图所示,将刻度尺直立在装满某种透明液体的宽口瓶中(液体未漏出),从刻度尺上A、B两点射出的光线AC和BC在C点被折射和反射后都沿直线CD传播,已知刻度尺上相邻两根长刻度线间的距离为1 cm,刻度尺右边缘与宽口瓶右内壁间的距离d=2.5 cm,由此可知,瓶内液体的折射率n= (可保留根号).
![]() 14.(4分)如左图所示,波源S从平衡位置开始上下(Y轴方向)振动,产生的简谐波向右传播,经过0.1S后,P点开始振动,已知SP=2m,若以P点开始振动时刻作为计时的起点,下图为P点的振动图象,则下列说法正确的是
14.(4分)如左图所示,波源S从平衡位置开始上下(Y轴方向)振动,产生的简谐波向右传播,经过0.1S后,P点开始振动,已知SP=2m,若以P点开始振动时刻作为计时的起点,下图为P点的振动图象,则下列说法正确的是
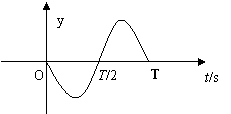 A.波源S最初是向上振动
A.波源S最初是向上振动
B.该简谐波的波速为20m/s
C.该波的周期为0.4s
D.该波的波长为20m
三、实验题: (24分)
15.(11分)
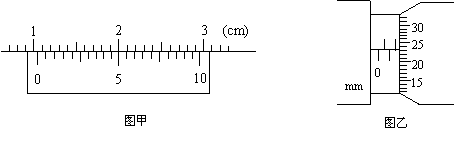
⑴ (4分)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图甲所示的读数是 mm.用螺旋测微器测量一根金属丝的直径,如图乙所示的读数是 mm.
 |
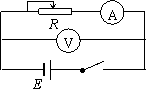 (2)(3分)为测定一节干电池的电动势和内阻,用如图所示电路.除干电池、开关、导线外可供使用的实验器材还有:
(2)(3分)为测定一节干电池的电动势和内阻,用如图所示电路.除干电池、开关、导线外可供使用的实验器材还有:
A.电流表(量程0.6A 3A)
B.电压表(量程3V 15V)
C.滑动变阻器(阻值范围0~10Ω 额定电流2A)
D.滑动变阻器(阻值范围0~200Ω 额定电流1A)
 请你完成下面的选择:电流表量程选_______,电压表量程选_______,滑动变阻器选_______.(填器材前面的字母代号)
请你完成下面的选择:电流表量程选_______,电压表量程选_______,滑动变阻器选_______.(填器材前面的字母代号)
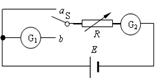
(3)(4分)某实验小组为测量一只微安表G1的内阻,采用了以下的方法:
实验器材:一只待测的微安表G1;一只标准电流表或量程较大(或与待测表相同)的标准微安表G2;一节干电池;0~9999Ω的电阻箱一只;单刀双掷开关一只;导线若干.
实验步骤一:将开关S断开,按图所示连接电路.
实验步骤二:使开关掷向b端,此时电路中通过微安表G1的电流较小,调节电阻箱R使微安表G1的示数接近满偏,记下此时电阻箱R的阻值R1和标准微安表G2的读数I.
实验步骤三:将开关掷向a端,并调节电阻箱R使标准微安表G2示数维持电流I不变,记下此时电阻箱R的阻值R2.
由以上步骤可以测得微安表G1的内阻为Rg=___________.
请指出该同学在实验中的疏漏:_________________________________________________.
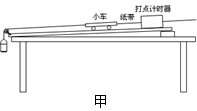 16.(13分)(1)在“探究恒力做功与动能改变的关系”实验中,某实验小组采用如图甲所示的装置.实验步骤如下:
16.(13分)(1)在“探究恒力做功与动能改变的关系”实验中,某实验小组采用如图甲所示的装置.实验步骤如下:
1把纸带的一端固定在小车的后面,另一端穿过打点计时器
2改变木板的倾角,以重力的一个分力平衡小车及纸带受到的摩擦力
3用细线将木板上的小车通过一个定滑轮与悬吊的砂桶相连
 4接通电源,放开小车,让小车拖着纸带运动,打点计时器就在纸带上打下一系列的点
4接通电源,放开小车,让小车拖着纸带运动,打点计时器就在纸带上打下一系列的点
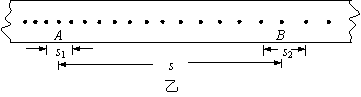
5测出s、s1、s2(如图乙所示),查得打点周期为T.
判断重力的一个分力是否已与小车及纸带受到的摩擦力平衡的直接证据是____________________________________________;
本实验还需直接测量的物理量是:__________________________.(并用相应的符号表示)
探究结果的表达式是____________________________________.(用相应的符号表示)
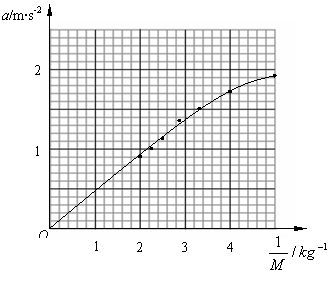
(2)用同样的装置做“探究加速度与力、质量的关系”实验.以下是一实验小组所获取的部分实验数据,根据表格中数据,在图中取合适的坐标系,作出图象.
 表格:小车受力相同(均取砂桶质量m=50g).
表格:小车受力相同(均取砂桶质量m=50g).
|
根据图象判断,实验产生误差的最主要原因是:________________________________.
四、计算或论述题:本题共 4小题,共67分.
17.(15分)如图所示,在汽车的顶部用不可伸长的细线悬挂一个质量m的小球,以大小为v0的初速度在水平面上向右做匀减速直线运动,经过时间t,汽车的位移大小为s(车仍在运动).求:
(1)汽车运动的加速度大小;
(2)当小球相对汽车静止时,细线偏移竖直方向的夹角(用反三角函数表示);
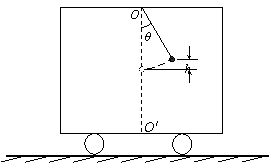 (3)汽车速度减小到零时,若小球距悬挂的最低点高度为h,O'点在O点的竖直下方.此后汽车保持静止,当小球摆到最低点时细线恰好被拉断.证明拉断细线后,小球在汽车水平底板上的落点与O'点间的水平距离s与h的平方根成正比.
(3)汽车速度减小到零时,若小球距悬挂的最低点高度为h,O'点在O点的竖直下方.此后汽车保持静止,当小球摆到最低点时细线恰好被拉断.证明拉断细线后,小球在汽车水平底板上的落点与O'点间的水平距离s与h的平方根成正比.
18.(17分)如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面夹角α=30°,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨电接触良好,金属棒的质量为m、电阻为R.两金属导轨的上端连接右端电路,灯泡的电阻RL=4R,定值电阻R1=2R,电阻箱电阻调到使R2=12R,重力加速度为g,现将金属棒由静止释放,试求:
(1)金属棒下滑的最大速度为多大?
(2)当金属棒下滑距离为S0时速度恰达到最大,求金属棒由静止开始下滑2S0的过程中,整个电路产生的电热;
(3)R2为何值时,其消耗的功率最大?消耗的最大功率为多少?
 |
19.(18分)如图甲所示,在边界MN左侧存在斜方向的匀强电场E1,在MN的右侧有竖直向上、场强大小为E2=0.4N/C的匀强电场,还有垂直纸面向内的匀强磁场B(图甲中未画出)和水平向右的匀强电场E3(图甲中未画出),B和E3随时间变化的情况如图乙所示,P1P2为距MN边界2.28m的竖直墙壁,现有一带正电微粒质量为4×10-7kg,电量为1×10-5C,从左侧电场中距MN边界![]() m的A处无初速释放后,沿直线以1m/s速度垂直MN边界进入右侧场区,设此时刻t=0, 取g =10m/s2.求:
m的A处无初速释放后,沿直线以1m/s速度垂直MN边界进入右侧场区,设此时刻t=0, 取g =10m/s2.求:
(1)MN左侧匀强电场的电场强度E1(sin37º=0.6);
(2)带电微粒在MN右侧场区中运动了1.5s时的速度;
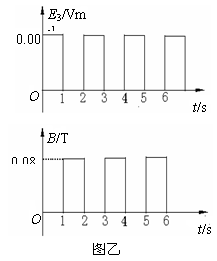 (3)带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?(
(3)带电微粒在MN右侧场区中运动多长时间与墙壁碰撞?(![]() ≈0.19)
≈0.19)
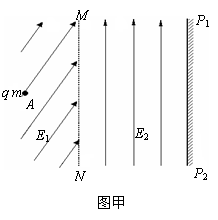
20、(17分)如图所示,将带电量Q=0.5C、质量m’=0.3 kg的滑块放在小车绝缘板的右端,小车的质量M=0.5 kg,滑块与绝缘板间的动摩擦因数μ=0.4,小车的绝缘板足够长,它们所在的空间存在着磁感应强度B=20 T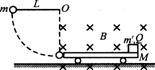 的水平方向的匀强磁场,磁场方向如图所示.开始时小车静止在光滑水平面上,一摆长L=1.25 m、摆球质量m=O.15 kg的摆从水平位置由静止释放,摆到最低点时与小车相撞,如图所示,碰撞后摆球恰好静止(g取10m/s2).求:
的水平方向的匀强磁场,磁场方向如图所示.开始时小车静止在光滑水平面上,一摆长L=1.25 m、摆球质量m=O.15 kg的摆从水平位置由静止释放,摆到最低点时与小车相撞,如图所示,碰撞后摆球恰好静止(g取10m/s2).求:
(1)摆球与小车的碰撞过程中系统损失的机械能△E;
(2)碰撞后小车的最终速度.
物理答案
一、选择题: 48分
1. D 2. C 3. C 4. B 5.BD 6. BC 7. BC 8. ABD 9. BC 10. AC 11. BC 12 . D
二、选作题:11分
13. (1) D (2)1.2
14. B
三. 实验题 24分
 15.(11分)
15.(11分)
(1)(4分)10.50; 1.731(1.730~1.733均给分)
(2)(3分)0.6A 3V C (每空1分)
(3)(4分)R2-R1 (2分)
实验步骤一中应补充:将电阻箱R阻值调到最大(或将电阻箱R阻值调到较大位置) (2分)
16.(13分)
(1)纸带上点迹间距相等 (2分)
小车的质量M、砂桶的质量m (2分)
![]() (3分)
(3分)
(2)图象见右图 (4分)
作为外力的砂桶质量太大 (2分)
四、计算或论述题:本题共 4小题,共67分.
17.(15分)解:
(1)由![]() 得
(2分)
得
(2分)
![]() (2分)
(2分)
(2)由受力分析得,小球受到重力与绳子拉力的合力大小 F=mgtanθ (1分)
根据牛顿第二定律,又 F=ma (1分)
所以 ![]() (2分)
(2分)
(3)设小球被细线拉着摆到最低点时的速度为v,
由机械能守恒定律得 ![]() (1分)
(1分)
所以 ![]() (1分)
(1分)
设细线断时小球距离汽车水平底板高度为H,细线断后小球作平抛运动
所以有 ![]() (1分)
(1分)
![]() (1分)
(1分)
解得 ![]() (3分)
(3分)
18.(17分)解:(1)当金属棒匀速下滑时速度最大,设最大速度为v,
达到最大时则有 mgsinθ=F安 (1分)
F安=ILB (1分)
![]() (1分)
(1分)
其中 R总=6R (1分)
所以 mgsinθ=![]() (1分)
(1分)
解得最大速度 ![]() (1分)
(1分)
(2)由能量守恒知,放出的电热 Q=![]() 2S0sinα-
2S0sinα-![]() (2分)
(2分)
代入上面的vm值,可得 ![]() (2分)
(2分)
(3)R2上消耗的功率 ![]() (1分)
(1分)
其中
![]() (1分)
(1分)
![]()
又 ![]() (1分)
(1分)
解以上方程组可得 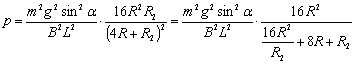 (2分)
(2分)
当![]() 时,R2消耗的功率最大
(1分)
时,R2消耗的功率最大
(1分)
最大功率![]() (1分)
(1分)
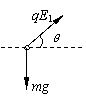 19.(18分)解:(1)设MN左侧匀强电场场强为E1,方向与水平方向夹角为θ.
19.(18分)解:(1)设MN左侧匀强电场场强为E1,方向与水平方向夹角为θ.
带电小球受力如右图.
沿水平方向有 qE1cosθ=ma (1分)
沿竖直方向有 qE1sinθ=mg (1分)
对水平方向的匀加速运动有 v2=2as (1分)
代入数据可解得 E1=0.5N/C (1分)
θ=53º (1分)
即E1大小为0.5N/C,方向与水平向右方向夹53º角斜向上.
(2) 带电微粒在MN右侧场区始终满足 qE2=mg (1分)
在0~1s时间内,带电微粒在E3电场中 ![]() m/s2 (1分)
m/s2 (1分)
带电微粒在1s时的速度大小为 v1=v+at=1+0.1×1=1.1m/s (1分)
在1~1.5s时间内,带电微粒在磁场B中运动,
周期为 ![]() s(1分)
s(1分)
在1~1.5s时间内,带电微粒在磁场B中正好作半个圆周运动.所以带电微粒在MN右侧场区中运动了1.5s时的速度大小为1.1m/s, 方向水平向左. (1分)
(3)在0s~1s时间内带电微粒前进距离 s1=
vt+![]() at2=1×1+
at2=1×1+![]() ×0.1×12=1.05m
×0.1×12=1.05m
带电微粒在磁场B中作圆周运动的半径 ![]() m (1分)
m (1分)
因为r+s1<2.28m,所以在1s~2s时间内带电微粒未碰及墙壁.
在2s~3s时间内带电微粒作匀加速运动,加速度仍为 a=0.1m/s2 ,
在3s内带电微粒共前进距离
s3=![]() m
(1分)
m
(1分)
在3s时带电微粒的速度大小为 ![]() m/s
m/s
在3s~4s时间内带电微粒在磁场B中作圆周运动的半径
![]() m=0.19m (1分)
m=0.19m (1分)
因为r3+s3>2.28m,所以在4s时间内带电微粒碰及墙壁.
 带电微粒在3s以后运动情况如右图,其中 d=2.28-2.2=0.08m (1分)
带电微粒在3s以后运动情况如右图,其中 d=2.28-2.2=0.08m (1分)
sinθ=![]() , θ=30º (1分)
, θ=30º (1分)
所以,带电微粒作圆周运动的时间为
![]() s (1分)
s (1分)
带电微粒与墙壁碰撞的时间为 t总=3+![]() =
=![]() s (1分)
s (1分)
20、(17分)解:(1)小球下摆过程,机械能守恒 mgL=![]() (2分)
(2分)
小球与小车相撞过程,动量守恒 mv0=Mv1(2分)
碰撞过程中系统损失的机械能
△E=![]() -
-![]() =1.3J(2分)
=1.3J(2分)
(2)设滑块与小车的最终相同速度V ,
动量守恒 Mv1=(M+m’)V= mv0(2分)
此时对滑块,洛仑兹力f=BQ V
而有 f>mg 滑块已离开小车(1分)
滑块离开小车时速度v2 ,则BQ v2=mg(2分)
小车此时速度v3,滑块与小车动量守恒
Mv1=M v3+m’ v2 = mv0(3分)
v3=![]() =1.3m/s(2分)
=1.3m/s(2分)
小车此后保持1.3m/s速度匀速运动(1分)