08届高三物理第三次周考试题
时间:90分钟 满分:100分
第Ⅰ卷(选择题 共40分)
一、选择题(本题每个小题中有1个或几个正确答案,每小题4分,共10小题,全部选对的得4分,选对但不全的得2分,选错或不选的得0分,共计40分)
1.关于匀加速运动,下面说法正确的是( )
A.位移与时间的平方成正比 B.位移总是随时间增加而增加
C.加速度、速度、位移三者方向一致 D.加速度、速度、位移的方向并不是都相同
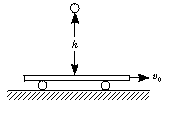
 2. 如图所示,小车开始静止于光滑的水平面上,一个小滑块由静止从小车上端高h处沿光滑圆弧面相对于小车向左滑动,滑块能到达左端的最大高度h/ ( )
2. 如图所示,小车开始静止于光滑的水平面上,一个小滑块由静止从小车上端高h处沿光滑圆弧面相对于小车向左滑动,滑块能到达左端的最大高度h/ ( )
A、等于h B、小于h
C、大于h D、停在中点与小车一起向左运动
3.关于单摆.下面说法正确的是( )
A.摆球运动的回复力是由摆线的拉力和重力的合力提供的
B.摆球运动过程中,经过同一点的速度是不变的
C.摆球运动过程中 加速度方向始终指向平衡位置
D.摆球经过平衡位置时.加速度不为零
 4. 如图所示,修建铁路、公路的路基时,允许的边坡倾角最大值叫做“自然休止角”,如果边坡超过自然休止角α会导致路基不稳定,关于α与土壤颗粒之间的动摩擦因数µ
的关系,下列说法中正确的是( )
4. 如图所示,修建铁路、公路的路基时,允许的边坡倾角最大值叫做“自然休止角”,如果边坡超过自然休止角α会导致路基不稳定,关于α与土壤颗粒之间的动摩擦因数µ
的关系,下列说法中正确的是( )
A.tanα>μ B.tanα<μ
C.tanα=μ D.α与μ无关
5.我国探月的嫦娥1号于11月5日到达绕月轨道,在不久的将来,我国宇航员将登上月球,假如宇航员在月球上测得摆长为L的单摆做小弧振动的周期为T,将月球视为密度均匀、半径为r的球体,则月球的密度为:( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 6. 如图所示,传送带与地面倾角为
6. 如图所示,传送带与地面倾角为![]() ,AB的长度为16m,传送带以10m/s的速度转动,在传送带上端A无初速度地放一个质量为0.5 kg的物体,它与传送带之间的动摩擦因数为0.5,求物体从A运动到B所用的时间可能为( ) (sin37°=0.6,cos37°=0.8,g=10m/s2).
,AB的长度为16m,传送带以10m/s的速度转动,在传送带上端A无初速度地放一个质量为0.5 kg的物体,它与传送带之间的动摩擦因数为0.5,求物体从A运动到B所用的时间可能为( ) (sin37°=0.6,cos37°=0.8,g=10m/s2).
A.1.8s B. 2.0s C. 2.1s D.4.0s
7. 如图所示,小船从A码头出发,沿垂直河岸的方向渡河,若河宽为d,渡河速度![]() 恒定,河水的流速与到河岸的最短距离x成正比,即V水=kx(x≤d/2,k为常量),要使小船能够到达距A正对岸为s的B码头,则( )
恒定,河水的流速与到河岸的最短距离x成正比,即V水=kx(x≤d/2,k为常量),要使小船能够到达距A正对岸为s的B码头,则( )
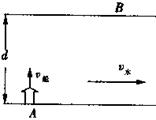 A.
A.![]() 应为
应为![]() B.
B.![]() 应为
应为![]()
C.渡河时间为![]() D.渡河时间为
D.渡河时间为![]()
|
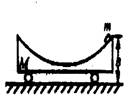
匀速运动,一个质量为m的小球从高h处自由下落,与小车碰撞
后,反弹上升的最大高度仍为h.设M >>m,发生碰撞时弹力N >>mg,
球与车之间的动摩擦因数为μ,则小球弹起后的水平速度可能是
( )
A.v0 B.μ![]() C.2
C.2![]() D.2μ
D.2μ![]()
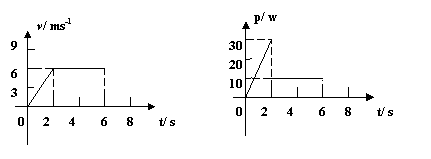 9. 一放在水平地面上的物体,受到水平拉力作用,在0—6s内其速度-时间图象和力F的功率-时间图象如图所示,则物体的质量为( )(取g=10m/s2)
9. 一放在水平地面上的物体,受到水平拉力作用,在0—6s内其速度-时间图象和力F的功率-时间图象如图所示,则物体的质量为( )(取g=10m/s2)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10. 如图所示,两物体A、B用轻质弹簧相连静止在光滑水平面上,现同时对A、B两物体施加等大反向的水平恒力F1、F2,使A、B同时由静止开始运动,在运动过程中,对A、B两物体及弹簧组成的系统,错误的说法是(整个过程中弹簧不超过其弹性限度)( )
 A.动量始终守恒
A.动量始终守恒
B.机械能始终守恒
C.当弹簧伸长到最长时,系统的机械能最大
 D.当弹簧弹力的大小与F1、F2的大小相等时, A、B两物速度零
D.当弹簧弹力的大小与F1、F2的大小相等时, A、B两物速度零
第Ⅱ卷(非选择题 共60分)
二、实验题(本题有2个小题,共10分)
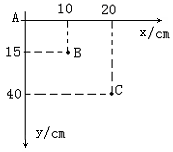
11.(3分) 在“研究平抛运动”实验中,某同学只记录了小
球运动途中的A、B、C三点的位置,取A点为坐标原点,则各
点的位置坐标如图所示,当g=10 m/s2时,下列说法正确的
是:( )
A.小球抛出点的位置坐标是(0,0)
B.小球抛出点的位置坐标是(-10,-5)
C.小球平抛初速度为2m/s
D.小球平抛初速度为1m/s
12.(7分)有一测量微小时间差的装置,是由两个摆长略有微小差别的单摆同轴水平悬挂构成.两个单摆摆动平面前后相互平行. (1)现测得两单摆完成 50次全振动的时间分别为 50.0 s和 49.0 s,则两单摆的周期差ΔT= s;
(2)某同学利用此装置测量小于单摆周期的微小时间差,具体操作如下:把两摆球向右拉至相同的摆角处,先释放长摆摆球,接着再释放短摆摆球,测得短摆经过若干次全振动后,两摆恰好第一次同时同方向通过某位置,由此可得出释放两摆的微小时间差.若测得释放两摆的时间差Δt=0.165s,则在短摆释放 s(填时间)后,两摆恰好第一次同时向 (填方向)通过 (填位置);
(3)若在利用单摆测当地重力加速度时,不慎形成了圆锥摆,如图所示.则所测得的重力加速度较真实值是 (填偏大、偏小)
三、计算题(本题有4个小题,共50分)
13.(8分)如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2秒钟通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据。(重力加速度g=10m/s2)求:(1)斜面的倾角a;(2)物体与水平面之间的动摩擦因数m;(3)t=0.6s时的瞬时速度v

14.( 10分
)2007年10月24日18时时零5分我国在西昌卫星发射中心成功发射了常娥1号绕月卫星,不久之后,将有中国的登月飞船到达月球.若某位宇航员随登月飞船登陆月球后,在月球某水平表面上方5m高处以速度v0 =
2.45m/s水平抛出一个小球,小球落回到月球表面的水平距离为6m.已知月球半径为R月=1737km,万有引力常量为G=6.67×10-11N·m2/kg2.(1)试求月球的质量M月 (2)若该宇航员把一座在月球上调整准确的摆钟拿回地球上来,则一昼夜将计时多少小时? (结果均保留2位有效数字,取![]() =2.45,地球上g=10m/s2)
=2.45,地球上g=10m/s2)
 15.(16分)如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离,设小球A、B与弹簧相互作用过程中无机械能损失,弹簧始终处于弹性限度以内(1)求当弹簧被压缩到最短时,弹簧的弹性势能E.(2)若开始时在小球B的右侧某位置固定一块挡板(图中未画出),在小球A与弹簧分离前使小球B与挡板发生正撞,并在碰后立刻将挡板撤走.设小球B与固定挡板的碰撞时间极短,碰后小球B的速度大小不变、但方向相反。设此后弹簧弹性势能的最大值为Em,试求Em可能值的范围.
15.(16分)如图所示,光滑水平面上,质量为2m的小球B连接着轻质弹簧,处于静止;质量为m的小球A以初速度v0向右匀速运动,接着逐渐压缩弹簧并使B运动,过一段时间,A与弹簧分离,设小球A、B与弹簧相互作用过程中无机械能损失,弹簧始终处于弹性限度以内(1)求当弹簧被压缩到最短时,弹簧的弹性势能E.(2)若开始时在小球B的右侧某位置固定一块挡板(图中未画出),在小球A与弹簧分离前使小球B与挡板发生正撞,并在碰后立刻将挡板撤走.设小球B与固定挡板的碰撞时间极短,碰后小球B的速度大小不变、但方向相反。设此后弹簧弹性势能的最大值为Em,试求Em可能值的范围.
16.(16分)如图所示,质量M=4kg的木板B静止于光滑的水平面上,其左端带有挡板,上表面长L=1m,木板右端放置一个质量m=2kg的木块A(可视为质点),A与B之间的动摩擦因素μ=0.2.现在对木板B施加一个水平向右的恒力F=14N,使B向右加速运动,经过一段时间后,木块A将与木板B左侧的挡板相碰撞,在碰撞前的瞬间撤去水平恒力F.已知该碰撞过程时间极短且无机械能损失,假设A、B间的最大静摩擦力跟滑动摩擦力相等,g取10m/s2.试求:
(1)撤去水平恒力F的瞬间A、B两物体的速度大小vA、VB分别多大;
(2)碰撞后瞬间A、B的速度大小vA,、vB,分别多大;
(3)最终A、B相对静止时木块A在木板上的位置。
![]()
一、选择题(每小题4分,共40分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| BD | A | D | C | B | BD | AC | AD | C | BD |
二、实验题(有2个小题,共10分)
11.(3分)BD(选对一个得2分) 12.(7分, (1)(3)每空2分(2)每空1分) 0.02 8.085 左 平衡位置 偏大
三、计算题(有4个小题,共50分)
13.( 8分)
解:(1)![]() ,又
,又![]() 。(3分)
。(3分)
(2)![]() (3分)
(3分)
(3)v=a1t=5×0.6=3m/s (2分)
14.(10分) 解:(1)h=g月t2/2 (1分) s=v0t (1分)
∴g月=2hv2/s2=10/6(m/s2) (1分)
又GM月= g月R2月 (1分)
∴M月=7.5×1022kg (1分)
(2)t=24![]() =59(h)
(5分)
=59(h)
(5分)
15.(16分)解:(1)当A球与弹簧接触以后,在弹力作用下减速运动,而B球在弹力作用下加速运动,弹簧势能增加,当A、B速度相同时,弹簧的势能最大.
设A、B的共同速度为v,弹簧的最大势能为E,则A、B系统动量守恒,有mv0=(m+2m)v (1分)
由机械能守恒 mv02/2=(m+2m)v2/2+E (2分) 联立两式得 E=mv02/3 (1分)
(2)设B球与挡板碰撞前瞬间的速度为vB,此时A的速度为vA
系统动量守恒mv0=mvA+2mvB (1分)
B与挡板碰后,以vB向左运动,压缩弹簧,当A、B速度相同(设为v共)时,弹簧势能最大,有: ![]() (1分)
(1分)
∴ ![]() (1分)
(1分)
又 ![]() (1分)
(1分)
所以 ![]() (1分)
(1分)
当弹簧恢复原长时与小球B挡板相碰,vB有最大值![]() ,有:
,有:
![]() (1分)
(1分)
![]() (1分)
(1分)
解得 ![]() =2v0/3 (1分)
=2v0/3 (1分)
即vB的取值范围为 0<VB ≤2v0/3 (1分)
当vB=v0/4时Em有最大值为Em1=mv02/2 (1分)
当vB=2v0/3时,Em有最小值为Em2=mv02/27 (1分)
所以, mv02/27≤ Em ≤mv02/2 (1分)
16.(16分)解:(1)设力F作用时间为t,则![]() ………………1分
………………1分
![]() …………………………………………………1分
…………………………………………………1分
依题意,有![]() …………………………………………………2分
…………………………………………………2分
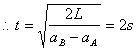 ………………………………………………………………1分
………………………………………………………………1分
故![]() ,
, ![]() ……………………………………1分
……………………………………1分
(2)A、B组成的系统动量守恒,有
![]() ……………………………………………………2分
……………………………………………………2分
由机械能守恒,有
![]() ……………………………………………2分
……………………………………………2分
解 得![]() …………………………………………………1分
…………………………………………………1分
(3)设最终A停在距B左端![]() 处,则由系统动量守恒定律,有
处,则由系统动量守恒定律,有
![]() …………………………………………………1分
…………………………………………………1分
根据能量守恒定律,有
![]() ……………………………2分
……………………………2分
解得:![]() ,
, ![]() ………………………………………………2分
………………………………………………2分