高三物理总复习素能双测单元同步卷(六)
动 量
一、选择题(每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,请将正确选项填在括号内)
1.航天飞机利用喷出的气体进行加速,是利用了高速气体的哪种作用( )
A.产生的浮力 B.向外的喷力
C.反冲作用 D.热作用
2.玻璃杯从同一高度落下,掉在水泥地上比掉在海绵上容易碎,这是由于玻璃杯与水泥地撞击过程中 ( )
A.玻璃杯的动量较大 B.玻璃杯受到的冲量较大
C.玻璃杯动量变化较大 D.玻璃杯的动量变化较快
3.有一则“守株待兔”的古代寓言,设兔子的头部受到大小等于自身重力的打击力时,即可致死.假设兔子与树桩作用时间大约为0.2秒,则若要被撞死,兔子奔跑的速度至少为 ( )
A.1m/s B.1.5m/s C.2m/s D.2.5m/s
4.如果物体在任何相同的时间内受到的冲量都相同,则物体的运动可能是( )
A.简谐运动 B.匀变速直线运动
 C.匀变速曲线运动 D.匀速圆周运动
C.匀变速曲线运动 D.匀速圆周运动
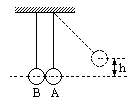
5.如图所示,两小球A、B均用细线吊在天花板上,且mA=4mB,当小球A从高为h处由静止开始向下摆动到最低点时,恰好与小球B正碰,关于碰后B球能升起的高度,以下数据中不可能的是 ( )
A.0.5h B.0.8h C.h D.2.5h
6.子弹以水平速度v0射向原来静止在光滑水平面的木块,并留在木块中和木块一起运动,在子弹和木块相互作用的过程中,下列说法正确的是( )
A.子弹速度的减少一定等于木块速度的增加
B.子弹动量的减少一定等于木块动量的增加
C.子弹动能的减少一定等于木块动能的增加
D.子弹对木块的冲量的大小一定等于木块对子弹的冲量大小
7.如图所示的装置中,木块B与水平桌面间的接触是光滑的,子弹A沿水平方向射入木块后留在木块内,将弹簧压缩到最短.现将子弹、木块和弹簧合在一起作为研究对象(系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中( )
![]() A.动量守恒、机械能守恒
A.动量守恒、机械能守恒
B.动量不守恒、机械能不守恒
C.动量守恒、机械能不守恒
D.动量不守恒、机械能守恒
8.一粒钢珠从静止状态开始自由下落,然后陷入泥潭中.若把在空中下落的过程称为过程I,进入泥潭直到停止的过程称为过程Ⅱ,则 ( )
A.过程I中钢珠的动量的改变量等于重力的冲量
B.过程Ⅱ中阻力的冲量的大小等于过程I中重力的冲量的大小
C.I、Ⅱ两个过程中合外力的总冲量等于零
D.过程Ⅱ中钢珠的动量的改变量等于零
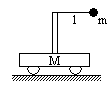 9.如图所示,绳长为l,小球质量为m,小车质量为M,将m拉至水平右端后放手,则(水平面光滑) ( )
9.如图所示,绳长为l,小球质量为m,小车质量为M,将m拉至水平右端后放手,则(水平面光滑) ( )
A.系统的动量守恒
B.水平方向任意时刻m与M的动量等大反向
C.m不能向左摆到原高度
D.M向右移动的最大距离为2lm/(M+m)
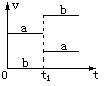 10.在光滑的水平面上,有a、b两物体质量分别为ma和mb,在t1时刻发生正碰,碰撞过程无机械能损失,两物体碰撞前后的速度图象如图所示,下列关系中正确的是
10.在光滑的水平面上,有a、b两物体质量分别为ma和mb,在t1时刻发生正碰,碰撞过程无机械能损失,两物体碰撞前后的速度图象如图所示,下列关系中正确的是
A.ma>mb B.ma<mb
C.ma=mb D.A、B两选项都可能
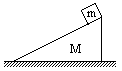 11.如图所示,质量为M的斜面放在光滑的水平面上,质量为m的物体由静止开始从斜面的顶端滑到底端,在这过程中 ( )
11.如图所示,质量为M的斜面放在光滑的水平面上,质量为m的物体由静止开始从斜面的顶端滑到底端,在这过程中 ( )
A.M、m组成的系统满足动量守恒
B.m对M的冲量等于M的动量变化
C.m、M各自的水平方向动量的增量的大小相等
D.M对m的支持力的冲量为零
12.如图所示,在光滑水平面上紧挨着放置A、B两长方体物块,一颗子弹(可视为质点)沿水平直线射穿物块A并停留在物块B内.设子弹在两物块内运动时所受阻力大小恒定.已知:A、B两物块的质量分别为MA和MB,子弹的质量为m;子弹进入物块A之前,其速度为V0;两物块分离时A已移动的位移为s1,此后B继续移动位移s2。后子弹与物块B相对静止;物块A和B长度均为L.根据上述已知条件 ( )
①可以求得物块A和B最终的速度vA和vB;
②可以求得子弹在物块A和B内相对运动的时间ΔtA和ΔtB;
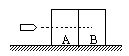 ③可以求得子弹在B物块内进入的深度d;
③可以求得子弹在B物块内进入的深度d;
④可以求得子弹在两物块内运动时所受阻力f的大小.
A.①、②、③、④都可以
B.只有①、③
C.只有①、②、④
D.只有③、④
二、实验填空题.(按题目要求作答,将答案填在相应空白处)
13.—个质量为m的物体,从静止开始沿倾角为θ的光滑斜面下滑,在物体速度由0增至v的过程中,斜面对物体弹力的冲量的大小为____。
![]() 14.如图所示,质量为m的物体,与水平地面之间的动摩擦因数为μ,在水平拉力F的作用下,物体从静止开始做加速运动,经过一段时间后撤去拉力F,物体又滑行一段时间后停下,若整个运动过程所用的时间是t,则物体在全程中的位移大小是____.
14.如图所示,质量为m的物体,与水平地面之间的动摩擦因数为μ,在水平拉力F的作用下,物体从静止开始做加速运动,经过一段时间后撤去拉力F,物体又滑行一段时间后停下,若整个运动过程所用的时间是t,则物体在全程中的位移大小是____.
15.载人气球原静止于高h的高空,气球质量为M,人的质量为m,若人沿绳梯滑至地面,则绳梯长至少为____。
16.某同学用图(1)所示装置通过半径相同的A、B两球的碰撞来验证动量守恒定律,图中PQ是斜槽,QR为水平槽.实验时先使A球从斜槽上某一固定位置G由静止开始滚下,落到位于水平地面的记录纸上,留下痕迹.重复上述操作10次,得到10个落点痕迹.再把B球放在水平槽上靠近槽末端的地方,让A球仍从位置G由静止开始滚下,和B球碰撞后,A、B球分别在记录纸上留下各自的落点痕迹。重复这种操作10次.图(1)中O点是水平槽末端R在记录纸上的垂直投影点.B球落点痕迹如图(2)所示,其中米尺水平放置,且平行于G、R、O所在的平面,米尺的零点与O点对齐.
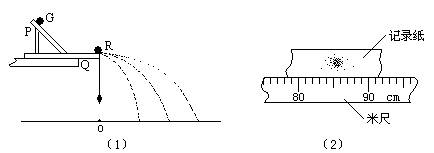
(1)关于实验中必须满足的条件,下列说法正确的是( )
A.A球的质量不小于B球的质量
B.斜槽末端必须水平
C.斜面必须光滑
D.碰撞必须是对心正碰
(2)碰撞后B球的水平射程应取为____cm.
(3)在以下选项中,哪些是本次实验必须进行的测量?
答:__________(填选项号).
A.水平槽上未放B球时,测量A球落点位置到O点的距离
B.A球与B球碰撞后,测量A球落点位置到O点的距离
C.测量A球或B球的直径
D.测量A球和B球的质量(或两球质量之比)
E.测量G点相对于水平槽面的高度
三、论述计算题(解答应写出必要的文字说明、方程和重要演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.)
![]() 17.如图所示,物块A、B质量分别为mA,、mB,用细绳连接,在水平恒力F的作用下A、B一起沿水平面做匀速直线运动,速度为v,如果运动过程中,烧断细绳,仍保持力F大小方向不变,则当物块B停下来时,物块A的速度为多大?
17.如图所示,物块A、B质量分别为mA,、mB,用细绳连接,在水平恒力F的作用下A、B一起沿水平面做匀速直线运动,速度为v,如果运动过程中,烧断细绳,仍保持力F大小方向不变,则当物块B停下来时,物块A的速度为多大?
18.蹦床是运动员在一张绷紧的弹性网上蹦跳、翻滚并做各种空中动作的运动项目.一个质量为50kg的运动员,从离水平网面3.2m高处自由下落,着网后沿竖直方向蹦回到离水平网面5.0m高处.已知运动员与网接触的时间为1.0s.若把在这段时间内网对运动员的作用力当作恒力处理,求此力的大小.(g=10m/s2)
19.在某城市的近郊发生一起两汽车迎面相撞的交通事故,经交警勘察情况如下,两车的车头紧紧咬合在一起,甲车驾驶室被撞坏,损坏的速度计指针定格在36km/h的示数上,甲、乙两车在相撞前已刹车,刹车痕迹长各为1.0m和0.9m,碰后两车在乙车前进的方向留下的痕迹长为1.6m,已知甲、乙两车质量分别为10吨和8吨,与地面的动摩擦因数均为0.5,重力加速度取10m/s2,请根据这些情况求:
(1)乙车在刹车前行驶的速度.
(2)在碰撞过程中,因甲车上的驾驶员使用了安全带仅受轻伤,若驾驶员质量为50kg,在此过程中安全带与人的作用时间延长为0.4s,求此驾驶员所受安全带的平均冲力大小.
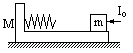
20.如图所示,质量为M=3kg,长度为L=1.2m的木板静止在光滑水平面上,其左端的壁上有自由长度为L0=0.6m的轻弹簧,右端放置一质量为m=1kg的小物块,小物块与木块间的动摩擦因数为μ=0.4,今对小物块施加一个水平向右的瞬时冲量I0=4N·s,小物块相对于木板向左运动而压缩弹簧使弹性势能增大为最大值Emax,接着小物块又相对于木板向右运动,最终恰好相对静止于木板的最右端,设弹簧未超出弹性限度,并取重力加速度为g=10m/s2.求:
(1)当弹簧弹性势能最大时小物块速度v;
(2)弹性势能的最大值Emax及小物块相对于木板向左运动的最大距离Lmax.
参考答案:
1、C 2、D 3、C 4、BC 5、A 6、BD 7、B 8、AC 9、BD 10、A 11、BC 12、A
13、 mvcotθ
14、(F-μmg) μgt2/2F
15、(M+m)h/M
16、(1)ABD (2)85.5cm(±0.5cm) (3)ABD
17、以A、B组成的系统作为研究对象.细绳烧断前,A、B一起做匀速直线运动,故系统所受外力之和为零.系统水平方向所受外力有拉力F,地面对物块A、B的摩擦力FfA、FfB,且F=FfA+FfB
绳烧断后至B停止运动前F与FfA、FfB均保持不变,故在此过程中系统所受外力之和仍为零,系统总动量保持不变.所以本题可用动量守恒定律求解.取初速度v的方向为正方向,绳断前为初状态,B停下瞬间为末状态,则由动量守恒定律,得(mA+mB)v=mAvA+mB×0,所以vA= (mA+mB)v/mA
18、将运动员看作质量为m的质点,从h1高处下落
刚接触网时速度的大小v1=![]() =10m/s (向下)
=10m/s (向下)
弹跳后到达的高度为h2,
刚离网时速度的大小v2=![]() =8m/s (向上)
=8m/s (向上)
以Δt表示接触时间,接触过程中运动员受到向上的弹力F和向下的重力mg, 规定向上为正方向由动量定理得:(F-mg)Δt=mv2-(-mv1)
由以上各式解得:F=mg+m![]()
代人数值得:F=1400N
19、(1)对甲乙车,设乙车运动的方向为正方向,因碰撞内力远大于外力,故系统动量守恒,-M1v1+M2v2=(M1+M2)v
又因v=![]() =4m/s,由以上方程v2=21.5m/s,乙车刹车后做匀减速运动其加速度为a=μg,乙车刹车前的速度v2′=
=4m/s,由以上方程v2=21.5m/s,乙车刹车后做匀减速运动其加速度为a=μg,乙车刹车前的速度v2′=![]() =21.7m/s
=21.7m/s
(2)对甲车上驾驶员Ft=-mv-mv1,以v1方向为正,代入数据得F=-1750N,(负号表示力的方向与v1的方向相反)
20、(1)对m据动量定理有I0=mv0
当二者速度相同时(设为v),弹性势能最大,对系统由动量守恒定律得mv0=(M+m)v
联立可解得:v=1m/s
(2)最终二者有相同速度(即为u),由动量守恒和功能关系得
mv0=(m+M)u
![]()
![]()
联立可解得:Emax = 3J Lmax = 0.75m