高三物理专题三直线运动（一）

北　京　四　中

　　年　级：高　三　　科　目：物　理　
　　责　编: 张丽刚　　录　入：张艳红

高三物理专题三 直线运动（一）

　　综合评述
　　1．匀变速直线运动是运动学的基础
　　（1）恒力作用下的直线运动，就是匀变速直线运动。
　　（2）典型的匀变速直线运动有：①只受重力作用的物体的自由落体运动和竖直上抛运动；②带电粒子在匀强电场中由静止开始被电场加速，或带电粒子沿着平行于电场方向射入电场中的运动；③静止的（或运动中的）物体、带电粒子、封闭着一定质量气体的玻璃管或气缸……所受的各种外力的合力恒定，且合力方向与初速度方向平行时的运动。

　　2、匀变速直线运动的规律，也是研究恒力作用下的曲线运动、圆周运动、动量守恒系统中物体的运动……所运用的，这些知识既是中学物理的重点，也是高考重点，应能熟练掌握、灵活运用。

　　高考视角
　　运动学在中学物理中占有较大的比重，内容包括直线运动、抛体运动、圆周运动和振动，其中有恒力作用下的运动，也有变力作用下的运动．在考试中既有单独命题考查的，也有与其他知识相综合考查的．在运动学方面，主要考查对运动过程的分析能力．
　　在直线运动中，热点主要是匀变速直线运动，由于它是研究其他运动的基础，而且公式较多，考查的热点也正是对这些知识的灵活运用，如 等的应用．自由落体运动是匀变速直线运动的特例；它的运动时间由高度决定，也常作为考查的重点．

　　范例精析
　　例1、一个小球由静止开始沿斜面下滑，经3s进入一个水平面，再经6s停下，斜面与水平面交接处的能量损失不计，则小球在斜面上和水平面上的位移大小之比是 (　　)
　　A．1：1 　B．1：2 　C．1：3 　D．2：1

　　思维过程　
　　思路一：假设在小球上物体的加速度为a₁，在水平面上小球的加速度为a₂，小球在斜面由静止下滑，做匀加速运动到达交接处达到一定的速度，又匀减速到速度为0，有a₁t₁=a₂t₂，找出a₁和a₂的关系，代入，即可解得．
　　解析一：由斜面到底端有 ①
　　由交接处到静止(可假设物体由静止到交接处)有：
　　 ②
　　又有 a₁t₁=a₂t₂， ③
　　由①②③得：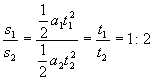
　　所以B选项正确．
　　思路二：小球从静止开始下滑，做匀加速运动到达交接处时速度达到最大v₁，这一段的平均速度为 ，后一段由速度最大达到零，平均速度也是 ，由s=vt，即可求得．
　　解析二： ．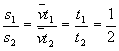
　　所以，选项B正确．

　　误区点拨　
　　本题条件较少，既不知斜面倾角，也不知各段的动摩擦因数．表面看来较为复杂，当然可以用假设参量来计算推导，但是用平均速度求解可以简化这个过程．

　　思维迁移　
　　灵活运用 (在匀变速直线运动中)会使我们的解题迅速而又准确．

　　变式题：
　　如图1—56所示，一小球从A点由静止开始沿斜面匀加速滑下，然后沿水平面匀减速运动到C停止．已知AB长s_l，BC长s₂，小球从A经B到C共用时间为t，试分别求出小球在斜面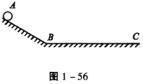上和在水平面上运动时加速度的大小．
　　答案：

　　例2、跳水运动员从离水面l0m高的平台上向上跳起，举双臂直起离开台面，此时其重心位于从手到脚全长的中点，跃起后重心升高了0.45m，达到最高点，落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)，从离开跳台到手触水面，他可用于完成空中动作的时间是____________s．(计算时可以把运动员看作全部质量集中在重心的一个质点，g取10m/s²，结果保留三位有效数字)

　　思维过程　
　　思路：运动员跳起时，脚在下，手在上，落水时，手在下，脚在上，在空中做各种花样动作，并不影响整体下落的时间，运动员从离开平台到落水分为两个阶段，一个是竖直上抛运动，另一过程是自由落体运动，分别求出t₁和t₂，即为运动员完成空中动作的时间．
　　解析：运动员跳起达到最高点的时间为
　　人从最高点下落至水面的高度是(10+0.45)m，可看成是自由落体运动，时间为
　　
　　∴t=t₁+t₂=0.3+1.4=1.7s．

　　误区点拨　
　　学生对于质点的运动规律较为熟练．本题中运动员在空中要做各种花动作，显然不能看作一个质点，但仍要用质点的知识处理，如何转化为一个质点的问题，即使题中已作出提示，抽象为一个模型的能力也是本题的考查点．

　　思维迁移　
　　高中物理研究的是最简单、最基本的规律，生活中的各种现象是纷繁复杂的，但这些现象都可以看做或抽象成某种物理规律或几种规律的综合，学习中应注意与生活实际相结合，从实践中总结规律，再用规律去解释生活中的物理问题．

　　变式题：　
　　跳伞运动员做低空跳伞表演，当飞机离地面224m水平飞行时，运动员离开飞机在竖直方向做自由落体运动。运动一段时间后，立即打开降落伞，以后运动员以12.5m／s²的平均加速度减速下降，为了运动员的安全，要求运动员落地速度最大不得超过5m／s(g取10m／s²)．问：
　　(1)运动员展伞时，离地面的高度至少为多少?着地时相当于从多高处自由落下?
　　(2)运动员在空中的最短时间为多少?
　　 答案：(1)99m， 1.25m； (2)8.6s．

　　例3、一艘小艇从河岸的A处出发渡河，小艇保持与河岸垂直方向行驶，经过10min到达正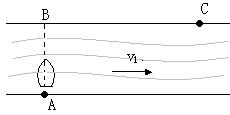对岸下游120m的C处，如图所示。如果小艇保持原来的速度逆水斜向上游与河岸成α角方向行驶，则经过12.5min恰好到达正对岸的B处，求河的宽度。

　　思维过程　
　　分析：设河宽为d，河水流速为v₁，船速第一次为v₂，第二次为v’₂，（v₂、 v’₂大小相同，方向不同）船两次运动速度合成如图所示，由题意有：
　　d＝v₂·t₁=v’₂·sinα·t₂ ①
　　S_BC=v₁·t₁ ②
　　 ③
　　三式联立，代入数据可求得：河宽d=200m

　　误区点拨　
　　本题是一道运动的合成与分解的实际问题，搞清哪个是合运动，哪个是分运动是处理这类问题的关键．

　　思维迁移　
　　对小船渡河的典型情况，要能熟练掌握并画出其运动合成的矢量图，并应用其思路解决类似问题。

　　变式题　
　　1、一条宽为d的河流，河水流速为v₁，船在静水中的速度为v₂，问：
　　(1)要使船划到对岸时的时间最短，船头应指向什么方向？最短时间为多少？
　　(2)要使船划到对岸时的航程最短，船头应指向什么方向？最短航程是多少？
　　分析：船在河流中航行时，由于河水流动要带动船一起运动，船的实际运动是船在静水中的运动和船随水漂流的运动的合运动。所以，船的实际运动速度v是v₂与v₁的矢量和。
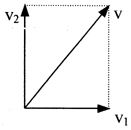
　　(1)当船头垂直指向对岸时，船在静水中的航速v₂垂直对岸，则船相对于水的分运动的位移最短，运动所需时间最短，如图所示。
　　最短时间
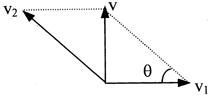
　　 (2)当v₂>v₁时，船头斜向上游与岸夹角为θ，船速v可垂直河岸，此时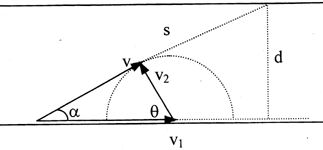航程最短为d，如图所示， ，即船头指向斜上游、与岸夹角 。
　　 当v₂<v₁时，用三角形法则分析，如图所示，当船速v的方向与圆相切时，v与岸的夹角α最大，航程最短。设航程最短为s，则由图可知 ，所以 船头指向斜上游，与岸夹角 。

　　当v₂=v₁时，如图所示，θ越小α越大航程越短，由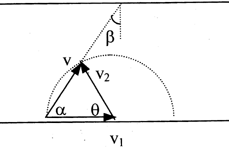图可知 ，而 ，所以 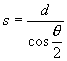。此时船头指向斜上游，与岸夹角为θ，航程 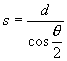，θ越小航程越短。当θ＝0时，s有最小值，等于d。但此时船速v＝0，渡河已经没有实际意义。所以，s只能无限趋近于d。

　　2.玻璃生产线上，宽9cm的成型玻璃板以2m／s的速度匀速向前行进，在切割工序处，金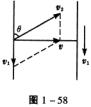钢钻的割刀速度为10m／s．为了使割下的玻璃板都成规定尺寸的矩形，金刚钻割刀的轨道应如何控制？切割一次的时间多长?
　　思路：如果玻璃板不动，垂直于玻璃板切割即可成矩形，而玻璃板匀速运动，要切割成矩形玻璃，即合运动的方向垂直于玻璃板的边缘，切割刀的运动和玻璃板的运动为分运动，利用运动的合成求解．
　　解析：如图1－58 v₁为玻璃板运动速度，v₂为切割刀的运动速度，v为合运动的速度，切割刀应与玻璃边缘成θ角逆向玻璃板运动方向切割，由图知
　　 　θ=arccos0.2
　　切割刀切割一次实际通过的位移为s=d/sinθ
　　切割用的时间为

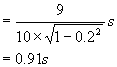
　　故金刚钻割刀应控制在与玻璃板运动方向相反成θ=arccos0.2的方向上，切割一次的时间为0.91s.