高三物理试题卷2

高三物理试题卷2

　例4、如图3-11所示。电子从A点由静止开始，经电压为U的电场加速后，从B点沿着与电场垂直的方向，射入宽度为l、场强为E的匀强电场中，经D点射离电场。电子射离电场时相对于射入电场方向的偏移距离为y，运动方向发生的偏折角为θ。下列说法正确的是（　　）
　　A、若加速电压U增大，则y和θ都增大
　　B、若加速电压U增大，则y减小、θ增大
　　C、若场强E增大，则y和θ都增大
　　D、若场强E增大，则y增大、θ减小

　　思维过程　
　　设电子的质量为m、电量为e；电子射入偏转电场时的初速度v，也就是经电压为U的电场加速后的速度v，根据动能定理，mv²=eU，得
　　设电子在偏转电场中的运动时间为t，则l=vt， ；消去上述两式中的t，并将v代入，得 ①
　　射离电场时运动方向偏折角的正切值为 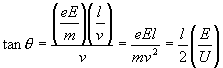②
　　（θ=arctan[]）
　　由y和θ（或tanθ）的表达式可知：U增大，y和θ都减小；E增大，y和θ都增大；可见，只有C正确。
　　（由①式和②式可以推得：y=tanθ。在图3-11中，将v_t反向延长，与v的方向相交于C点，在直角三角形CFD中， FD=y。上述事实说明：带电粒子沿着与电场垂直的方向射入匀强电场中，当带电粒子离开匀强电场时，都好像是从电场中心处沿直线射出似的。）

　　误区点拨　
　　公式推导要推到最终形式才能判断

　　思维迁移　
　　位移、速度求出来之后，相应的能量计算就较方便了。

　　变式题　
　　1. 带电粒子以初速度v₀沿着与电场垂直的方向射入匀强电场中，射离匀强电场时，带电粒子的运动方向与射入电场时的运动方向发生的偏折角等于θ，则带电粒子通过电场的过程中动能的改变量多大？
　　[解析]设带电粒子的质量为m，则射入匀强电场时的初动能为E_k0=mv₀²
　　带电粒子射离匀强电场时，若沿电场方向的速度分量为v，则v=v₀tanθ，射离电场时的速度大小为
　　E_kt=mv_t²=mv₀²（1+tan²θ）=E_k0（1+tan²θ）
　　可见，通过电场的过程中，带电粒子的动能增加了，动能的改变量为
　　ΔE_k=E_kt-E_k0=E_k0tan²θ

　　2. 如图3-13所示，质量为m=5×10^-8kg的带电粒子，以初速度v₀=3m/s，从水平放置的平行金属板的正中同射入两板之间的匀强电场中，已知两板长l=10cm，两板相距d=1cm，当两板间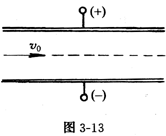电压U=1.5×10²V时，带电粒子恰好能沿水平直线匀速穿过，现改变两板间的电压，试分析计算，电压值在什么范围内变化时，该带电粒子总能从两板之间离开电场？
　　[解析]由图3-13可知，粒子带负电，设电量为q，匀速穿过电场时，所受电场力等于重力；q=mg，则粒子的带电量为q=×10^-10C
　　带电粒子通过电场所花时间为
　　带电粒子从上板边缘射离电场时，对应着两板间电压的最大值U₁满足方程
　　 　解得 U₁=285V
　　带电粒子从下板边缘射离电场时，对应着两板间电压的最小值U₂满足方程
　　 　解得 U₂=15V
　　综上所术，两板间的电压变化范围应该是285V≥U≥15V

　　小结　
　　此类问题用平抛规律来解。即：两个运动的合成。注意合力一般是重力和电场力的合力。

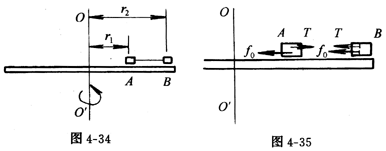
　例5、在绕竖直轴匀速转动的水平圆盘上，沿一条半径放置的A、B两个物体，质量均为m，A、B与转轴间的距离分别r₁和r₂，这时连接A、B的细线沿水平方向被拉直（如图4-34）。已知A、B与圆盘间的最大静摩擦力为f₀。
　　现逐渐增大转速。在A、B刚要开始滑动前的瞬间，烧断连接A、B间的细线，圆盘开始以该时刻的转速匀速转动。试问：该时刻圆盘转动角速度多大？细线烧断后A、B将如何运动？
　　　　
　　思维过程
　　在A、B即将开始滑动时，A、B受到圆盘沿水平方向指向圆心的，最大静摩擦力作用；设这时细线中的拉力为T，则A、B的受力情况如图4-35所示。它们的运动方程分别为
　　A： mω²r₁=f₀-T
　　B： mω²r₂=f₀+T
　　两式相加，得mω²(r₁+r₂)=2f₀，可知A、B即将开始滑动前瞬间圆盘转动角速度
　　
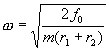
　　细线烧断后，线对A、B的拉力消失。由于以角速度 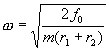匀速转动时，A需要的向心力小于f₀，B需要的向心力大于f₀，所以细线烧断后，A仍相对圆盘静止、跟圆盘作匀速转动（角速度为ω），而B则发生离心现象，相对于圆盘发生滑动。

　　误区点拨　
　　A、B不是同时到达最大静摩擦，随着ω的增加，B先到达最大静摩擦，然后拉力出现，A逐渐到达最大静摩擦，此时是本题的临界状态。所以，在此时，AB所受的摩擦皆为最大静摩擦。

　　思维迁移　
　　圆周运动的题主要是合力提供向心力。找到向心力是解题的关键。

　　变式题
　　1． 一内壁光滑的环形细圆管，位于竖直平面内，环的半径为R（比细管的直径大很多）。在圆管中有两个直径与细管内径相同的小球（可视为质点），A球的质量为m₁，B球质量为m₂，它们沿环形圆管道顺时针方向运动，经过最低点时的速度都为v₀，设A球运动到最低点时，B球恰好运动到最高点，若要此时两球作用于圆管的合力为零，那么m₁、m₂、R与v₀应满足的关系式是_________。
　　（本题是1997年全国高考统一试题第21题）
　　[解析] A球在通过最低点时，对圆管的压力竖直向下，设大小为N₁；根据牛顿第三定律，小球A受到圆管的支持力（竖直向上）大小也为N₁；小球通过最低点时的运动方程为 得
　　设B球通过最高点时速度为v，根据机械能守恒定律
　　得 m₂v²=m₂v₀²-4m₂gR
　　根据题意，B球通过最高点时，应该对圆管有竖直向上的压力（设大小为N₂）；根据牛顿第三定律，圆管对B球有竖直向下的压力，大小也为N₂；B球通过最高点时的运动方程为 得

　　要两个小球作用于圆管的合力为零，则应N₁=N₂；本题的正确答案是
　　 或

　　2． 水平放置的木柱，横截面为边长等于a的正四边形ABCD；摆长l=4a的摆，悬挂在A点（如图4-38），开始时质量为m的摆球处在与A等高的P点，这时摆线沿水平方向伸直；已知摆能够承受的最大拉力为7mg；若以初速度v₀竖直向下将摆球从P抛出，为使摆球能始终沿圆弧运动，并最后击中A点。求v₀的许可值范围。（不计空气阻力）。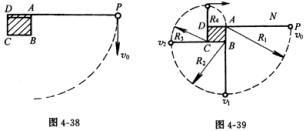
　　[解析] 根据题意可知，摆球先后依次以A、B、C、D、为圆心，R₁=4a、R₂=3a、R₃=2a、R₄=a为半径，各作四分之一圆周的圆运动。
　　摆球从P点开始，设半径R₁=4a运动到最低点时速度设为v₁，根据动能定理
　　 ①
　　当摆球开始以v₁绕B点以半径R₂=3a作圆周运动时，摆线受到的拉力最大，设为T_max=7mg。这时摆球的运动方程为
　　 ②
　　将①式中的mv₁²=mv₀²+8mga代入②式，可得v₀的最大许可值为 。
　　摆球绕C点以半径R₃=3a运动到最高点时，为确保沿圆周运动，到达最高点时的水平速度 。根据动能定理
　　 ③
　　得
　　综上所述，v₀的取值范围应为

　　

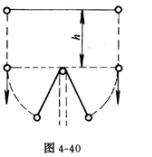　　3． 两个质量均为m的小球，用长度为l的细线相连，两手分别握住一个小球，使细线恰好能沿水平方向伸直（如图4-40），这时细线的中点正好处在沿水平方向固定着的细杆的正上方，细线与细杆互相垂直，两者之间的距离为h。细线能承受的最大拉力为T₀。
　　让两个小球同时开始自由落下，试问h多大时，在细线与细杆相碰后，细线才会被拉断？
　　[解析] 细线的中点碰到细杆后，小球即以细杆为圆心作半径 的圆周运动；在小球运动到最低点时，速度最大，细线受到的拉力也最大。
　　根据动能定理，可以求得小球运动到最低点时的速度v。
　　 ①
　　设小球运动到最低点时，细线上的拉力为T，则
　　 ②
　　① ②联立：
　　
　　可见，要使细线被拉断，细线与细杆之间的距离h应满足条件
　　
　　从上式可以看出，只有T₀>3mg上式才有意义；表明在T₀<3mg时，从上述高度自由下落时，小球还没有到达最低点时，线细就已经被拉断。
　　如要细线与细杆相碰时立即就被拉断，则
　　
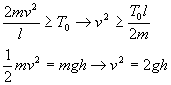
　　可见

　　4． 如图4-42所示。粗细均匀的U形玻璃管，三段直管的长度均为l，水平直管中有一段长度恰好等于l的水银柱。将右侧管口封住，让U形管以左侧管为轴匀速转动时，水银柱沿封口的一侧管子上升了 。设大气压强为p₀，水银密度为ρ，求匀速转动的角速度多大？
　　　　　　　　
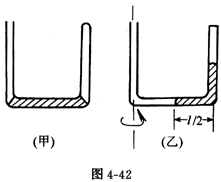
　　[解析] 以管中被封闭的空气为研究对象。开始时其体积V₁=lS，压强p₁=p₀；以角速度ω匀速转动时，体积 ，根据玻意耳定律，这时压强p₂=2p₀。
　　U形管匀速转动时，竖直管中长度为 的水银柱作匀速圆周运动所需向着心力，由玻璃管壁的支持力提供；水平管中长度为 的水银柱作匀速圆周运动所需向心力，由该段水银柱两端的压力的合力提供。
　　该段水银柱的质量 ，它的中心到转动轴的距离，即圆半径 ；若大气压强p₀以水银柱的高度表示，则该段水银柱两侧受到的压力指向转动轴的合力为 ；可见，它的运动方程为
　　得角速度： 。
　　（请注意：如要具体计算时，l应该用m（米）作单位，p₀应该用mHg（米汞柱）作单位，g取9.8m/s²或10m/s²。）
　　作为发散思维训练：如果让图4-42（甲）所示的U形玻璃管，沿水平方向向左作匀加速直线运动，加速度多大时水平直管中的水银柱沿封口的竖直管上升 高度？[答案 ]

　　小结　
　　圆周运动的合力可能会是多种性质的力的合力，包括气体的压力、万有引力、电磁场力等。

　　例6、地球的质量M=6.0×10²⁴kg、半径R=6.4×10⁶m、自转周期T=8.64×10⁴s，万有引力常量G=6.67×10^-11N·m²/kg²。假定地球是一个规则的球体。
　　（1）质量为m（kg）的物体，在地球表面上受到的地球对它的吸引力多大？
　　（2）质量为m（kg）的物体，在南、北极对水平地面的压力多大？在赤道上，对水平地面的压力多大？
　　（3）地球自转周期减小到多大时，赤道上的物体对地面的压力恰好减小为零？

　　思维过程　
　　（1）根据万有引力定律
　　（2）在赤道水平地面上的质量为m的物体，由于地球自转作匀速圆周运动，所需向心力为
　　静止在赤道水平地面上的物体受地球吸引力和地面支持力作用，它们的合力是向心力F_向心=F_万有-N
　　根据牛顿第三定律，该物体对水平地面的压力与地面对它的支持力大小相等、方向相反：N'=N=F_万有-F_向心=9.74m(N)。
　　静止在南、北极水平地面上的质量为m的物体不作圆周运动，它对水平地面的压力为9.77m(N)。
　　（3）设地球自转周期为T'时，赤道水平地面上的物体对地面压力减小为零，则
　　 得 。

　　误区点拨　
　　请注意：5082s也是人造地球卫星的最小周期。

　　思维迁移　
　　卫星运动的题，v、T是两个经常用到得量。由这两个量，可以较容易导出其它的物理量。

　　变式题　
　　1． 已知人造地球卫星运动的最小周期T_min=5082s，万有引力常量G=6.67×10^-11N·m²/kg²，试分析计算地球的平均密度。
　　[解析] 设地球质量为M，半径为R；人造地球卫星的质量为m，周期为T，轨道半径为r；则卫星绕地球的运动方程为 得 。设地球平均密度为ρ，则 ，将M代入T的表达式，得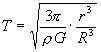
　　r=R时，人造地球卫星的周期最小，所以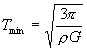
　　可见：地球的平均密度为

　　2． 我国在1984年4月8日成功地发射了一颗通讯卫星。这颗通讯卫星距地面的高度h=3.60×10⁴km，绕地球转动的角速度为ω₁、线速度为v₁；地球的半径R=6.4×10³km，自转角速度为ω₂、赤道上各点的自转线速度为v₂。则：
　　（1）ω₁：ω₂=________：_______；
　　（2）v₁：v₂=________：_______。
　　[解析] （1）通讯卫星一般是同步卫星，ω₁=ω₂，所以ω₁：ω₂=1：1。
　　　　　 （2）同步卫星的轨道半径r=R+h=4.24×10⁴km，同步卫星相对“静止”在赤道正上方，角速度相等，所以v₁：v₂=（R+h）：R=6.625：1。

　　3． 甲、乙两颗人造地球卫星，在同一轨道平面中绕地球同向作匀速圆周运动；甲距地面的高度h₁=0.5R，乙距地面的高度h₂=5R；上述R为地球半径。已知某时刻甲、乙两颗卫星之间的距离最小。
　　（1）甲、乙两颗卫星的线速度比v₁：v₂=________：_______；
　　（2）甲、乙两颗卫星的周期比T₁：T₂=________：_______；
　　（3）以乙卫星的周期（T₂）为量度时间的单位，至少要过________时间，两颗卫星相距最大。
　　[解析] （1）由 ，得 。r₁=1.5R，r₂=6R； .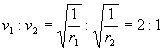
　　（2） .所以 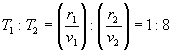。（甲卫星运动“快”）
　　（3）某时刻甲、乙两颗卫星之间距离最小，表明两颗卫星恰好处在地面某处的正上方，如图4—1（甲）所示。两颗卫星相距最远的情况如图4—1（乙）所示。
　　　　　
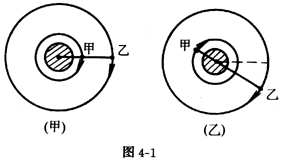
　　设甲、乙两颗卫星绕地球转动的角速度分别为ω₁与ω₂； ，所以ω₁：ω₂=T₁：T₂=8：1。显然，相距最大的条件是（ω₁-ω₂）t=（2n-1）π，n=1、2、……；n=1时得最短的时间
　　即至少要经过 时间，两颗卫星间的距离才最大。

　　小结　
　　这类题综合圆周运动和万有引力两部分知识，解这类题的一般思路是万有引力提供向心力。另外，这部分的计算较繁琐，需要注意。

　　例7、一质量为m、电量为q的带电粒子，在磁感强度为B的匀强磁场中作圆周运动，其效果相当于一环形电流。则此环形电流强度I=____________。
　　（本题是1991年全国高考统一试题第28题。）

　　思维过程　
　　带电粒子在匀强磁场中（垂直于磁场的平面里）作匀速圆周运动，如速度为v，则所受磁场力（洛仑兹力）f=Bqv，磁场力的方向与速度方向垂直，对带电粒子不做功，洛仑兹力的作用只是改变速度的方向，所以带电粒子一定作匀速圆周运动，磁场力为向心力，运动方程为
　　带电粒子作匀速圆周运动的轨道半径为 ，沿圆周运动的周期为 ，频率为 。
　　根据电流强度的定义 ，环形电流强度为

　　误区点拨　
　　电流强度I除了通过UR可以求出之外，还有其它很多的方法，它的定义 也是很重要的方法。

　　思维迁移　
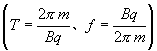　　1、带电粒子在匀强磁场中垂直于磁场的平面里作匀速圆周运动时，最显著的特征是：①轨道半径 与速度大小成正比；②运动周期和频率 均与速度大小无关。
　　2、带电粒子在匀强磁场中作圆周运动形成的环形电流强度 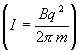也与带电粒子的速度无关。

　　变式题　
　　1．氢的同位素氕、氘、氚的原子核，在同一匀强磁场中作匀圆圆周运动，轨道半径相同，则：
　　（1）它们的动量值之比P₁：P₂：P₃=_________：_________：_________；
　　（2）它们的动能值之比E₁：E₂：E₃=_________：_________：_________。
　　[解析] 由运动方程 ，得 P=mv=BqR 氕、氘、氚的核带电量相等，B、R也相等，所以 P₁：P₂：P₃=1：1：1

　　（有的人根据 ，认为动能跟质量成反比，并写出E₁：E₂：E₃=m₃：m₂：m₁=3：2：1。请读者想一想，他错在哪些地方？他是怎样搞错的？）

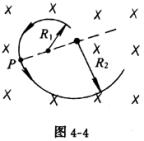
　　2． 如图4-4所示。一个质量为m、带电量为q的带电粒子，在匀强磁场中垂直于磁场方向的平面里做半径为R₁的匀速圆周运动；在P点该粒子吸收了若干个原来静止的电子后做半径为R₂的圆周运动；经测量R₂：R₁=2：1。试分析计算：该带电粒子在P点吸收了几个电子（设电子电量为e）？
　　[解析] 根据图中箭头所指示的运动方向，可知该粒子原来带正电（电量为q），在P点吸收了几个电子（设n个）后，仍带正电（设电量为q'），但所带电量减少了：q'=q-ne。
　　粒子原来带正电，其质量肯定远大于电子质量（带正电荷的质量最小的粒子是质子），吸收几个原来静止的电子后，质量和速率几乎没有发生变化。带电粒子在匀强磁场中作匀速圆周运动的轨道半径 与带电量成反比，可见 R₁：R₂=q'：q=(q-ne)：q=1：2 所以吸收的电子数n=q/2e。
　　（请注意：①n=1、2、……为正整数；②所以，粒子原来的带电量q=2ne肯定是“元电荷”的偶数倍，且是正电荷。读者可以把这道题目改变为选择题；试试看，为它配上四个选择项。学习改编题目，是一种积极、主动的学习方法。）

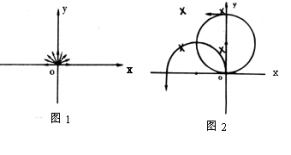
　　3．如下图1，在x轴的上方（y≥０）存在着垂直于纸面向外的匀强磁场，磁感应强度为Ｂ。在原点Ｏ有一个离子源向x轴上方的各个方向发射出质量为m电量为q的正离子，速率都为v。对那些在xy平面内运动的离子，重力不计。在磁场中可能到达的最大x＝_____________，最大y＝_____________。　　　　　　
　　解析：如右下图2，正离子在磁场中运动时，重力忽略，做匀速圆周运动，可能到达的最大x、y恰好是匀速圆周运动的直径。 ( )。
　　　　　　

　　小结　
　　两个粒子，带电量相等，在同一匀强磁场中只受磁场力而作匀速圆周运动（ BC）
　　A、若速率相等，则半径必相等
　　B、若质量相等，则周期必相等
　　C、若动量大小相等，则半径必相等
　　D、若动能相等，则周期必相等
　　（本题是1995年全国高考统一试题第16题。）

　　质子和α粒子在同一匀强磁场中作半径相同的圆周运动，由此可知质子的动能E_k和α粒子的动能E₂之比E₁：E₂等于（　B　）
　　A、4：1 B、1：1 C、1：2 D、2：1
　　（本题是1994年全国高考统一试题第10题。）

　　1、上述几道高考试题，都涉及带电粒子在匀强磁场中作匀速圆周运动的基本特征，这些基本特征都是来源于洛仑兹力的基本特性；①力的大小（f=Bqv）与速度大小成正比；②力的方向与速度方向垂直，不做功，不改变速度的大小，不改变动能。 。所以，了解力的基本特性，把握物体在力的作用下运动的基本特征，是十分重要的。
　　2、罗列上述几道高考试题的目的，除了说明了了解力的基本特性，把握运动的基本特征的重要性以外，还想说明：①基本知识的重要性。如质子与α粒子的质量比、电量比必须了解并能运用；②基本方法必须掌握。

　　例8、（2000全国高考题）一辆实验小车可沿水平地面(图1—72 中纸面)上的长直轨道匀速向右运动，有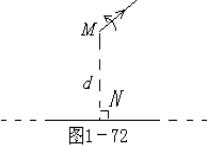一台发出细光束的激光器装在小转台M上，到轨道的距离MN为d＝10m，转台匀速转动，使激光束在水平面内扫描，扫描一周的时间为T=60s，光束转动方向如图中箭头所示，当光束与MN的夹角为45°时，光束正好射到小车上，如果再经过Δt＝2.5s，光束又射到小车上，则小车的速度为多少?(结果保留两位有效数字)

　　思维过程
　　思路：激光束所在的转台做匀速圆周运动，在Δt的时间内转过的角度Δφ的过程中，存在两种可能性，如图1—73所示，一种是小车正在接近N点，另一种是小车正在远离N点．
　　解析：在Δt内，光束转过角度
　　Δφ＝ 360°＝15° ①
　　有两种可能：
　　(1)光束照射小车时，小车正在接近N点，Δt时间内光束与MN的夹角由45°变为30°，小车走过L₁，速度应为
　　 ②
　　由图知：L₁=dtan45°-dtan30° ③
　　由②③两式代入数值，得v₁=1.7m／s．
　　(2)光束照射到小车时，小车正在远离N点，Δt内光束与MN的夹角从45°变为60°，小车走过L₂，速度为
　　 ④
　　由图可知：L₂＝dtan60°-dtan45° ⑤
　　由④⑤两式代入数值，得v₂＝2.9m／s：

　　误区点拨　
　　看不懂题目所描述的测速装置与测速原理，对示意图不理解，又不能把小车当质点看待，认为光束照射在小车上的光点随小车一起向右运动，混淆了小车的运动与光点的运动．

　　思维迁移　
　　分析小车运动存在的两种可能情形是本题的关键．

　　变式题　
　　1．一个小球做平抛运动，光源在抛出点在它前面有一块墙，正好映出它的影，请分析影是做什么运动？
　　答案：匀速直线运动

　　2、如图所示，点光源发出的光垂直射到平面镜M上，经反射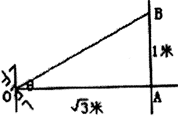在正对着平面镜相距为 米的墙上有一光斑，若使光斑沿墙向上移动1米，平面镜M应以O点为轴转过的角θ度是（C）
　　A、5° B、10° C、15° D、20°

　　3、如图所示，水平桌面上一点光源S，平面镜M与桌面成30°角。现保持光源不动，平面镜M以速度v竖直方向向上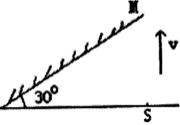平动，则点光源S在平面镜中的像将（E）
　　A、以速度v运动，方向与v相同
　　B、以速度2v运动，方向与v相同
　　C、以速度v运动，方向与v相同
　　D、以速度v运动，方向与v相同
　　E、以上说法都不正确

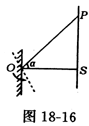　　4、如图18-16所示，竖直墙上有一点光源S，发出一束水平向左的光束射到平面镜上的O点，当平面镜绕过O点垂直纸面的轴，以角速度ω逆时针转动时，被平面镜反射的光在墙上形成的光点便沿墙运动。已知S与O点间的距离为d，试问当反射光与入射光间的夹角α=60°时，墙上光点P在这时刻沿墙运动的速度多大？
　　答案： 8ωd

　　小结　
　　光点（或影子、像等）的运动问题，要注意运动的合成和分解。一般情况下，光点实际的运动为合运动。
　　第4题中的光点在墙上的运动为合运动，可以分解为两个运动：垂直和平行于光线两个方向的运动。

　　回味反思
　　1.物体做曲线运动的条件是初速度方向和合力方向不在一条直线上。我们判断物体运动情况首先要做的便是判断合力。这也是牛顿定律作为经典物理学的基础的原因。
　　2.我们现在所谈的合力，已经不再局限在高一的重力、弹力、摩擦力三种力的合力，它还包括如万有引力、库仑力、洛仑兹力等我们在中学阶段学过的各种力。
　　3.我们七个专题围绕的一个中心便是力和运动的关系。从横向的角度来看待这些知识，可能会对知识的理解（特别是知识之间的联系）起到一定的作用。