高三物理模拟(六)
班级: 姓名:
一、单项选择题
1.设电子在运动过程中只受电场力作用,则在下述哪种电场中,只要初速度取合适的值,电子既可能始终沿某条电场线运动,也可能始终沿某个等势面运动
A.匀强电场 B.单位正电荷产生的电场
C.单位负电荷产生的电场 D.上述电场都不可以
2.目前普遍认为,质子和中子都是由被称为u夸克和d夸克的两类夸克组成.u夸克带电量为2e/3,d夸克带电量为-e/3,e为基元电荷.下列论断中可能正确的是
A.质子由1个u夸克和1个d夸克组成,中子由1个u夸克和2个d夸克组成
B.质子由2个u夸克和1个d夸克组成,中子由1个u夸克和2个d夸克组成
C.质子由1个u夸克和2个d夸克组成,中子由2个u夸克和1个d夸克组成
D.质子由2个u夸克和1个d夸克组成,中子由1个u夸克和1个d夸克组成
3.频率为ν的光子,具有能量hν,动量hν/C,将这个光子打在处于静止状态的自由电子上,光子将偏离原来的运动方向,这种现象称光子的散射,散射后的光子
A.虽然改变原来运动方向,但频率不变
B.由于从电子碰撞中获得能量,因而频率增大
C.散射后的光子运动方向将与电子运动在一条直线上,但方向相反
D.由于碰撞,散射后的光子频率低于入射光子的频率
4.如图4所示,ABCD是固定的水平放置的足够长U形金属导轨,整个导轨处于竖直向上的匀强磁场中,在导轨上放一金属棒ab,给ab一个水平向右的冲量,使它以初速v0运动起来,最后静止在导轨上,在导轨是光滑和粗糙两种情况下
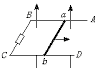
图4
A.安培力对ab所做的功相等 B.电流通过整个回路做功相等
C.整个回路产生的热量相等 D.到停止运动时,两棒运动距离相等
5.轮船在大海中航行,受到波浪的冲击力使轮船左右摇摆,可能使轮船倾覆,为了减弱这种左右摇摆,下列办法一定可行的是
①.改变轮船的航向 ②.改变轮船的航速
③.轮船的航向与波浪前进方向一致,减小正对面积,减小冲击力
④.轮船的航向与波浪前进方向相反,减小正对面积,减小冲击力
A.①② B.①②③④ C.③④ D.②③④
6.一只标有“220 V,60 W”的白炽灯泡,当用多用电表的欧姆挡去测它的电阻值时,测得的值约为
A.明显小于800 Ω B.接近1000 Ω C.明显大于800 Ω D.约800 Ω
7.在粗糙、绝缘且足够大的水平面上,固定一个带负电的点电荷Q,今有一质量为M的带电量为+q的小物体放在水平面上,并由静止释放,小物体沿远离Q的方向运动,最后停下来,则这一过程中:
A.电场力对小物体所做的功等于其增加的机械能;
B.小物体的电势能先减小后增大
C.小物体的加速度一直减小
D.电场力对小物体所做的功等于摩擦产生的热量.
8.为了利用海洋资源,海洋工作者有时根据水流切割地磁场所产生的感应电动势来测量海水的流速.假设海洋某处的地磁场竖直分量为B=0.5×10-4 T,水流是南北流向,如图8所示,将两个电极竖直插入此处海水中,且保持两电极的连线垂直水流方向.若两电极相距L=10 m,与两电极相连的灵敏电压表读数U=0.2 mV,则海水的流速大小为
A.4 m/s B.40 cm/s C.4 cm/s D.4 mm/s
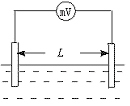
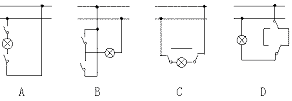
图8 图9
9.楼梯的照明灯可用楼上楼下两个开关中的任何一个都可使灯点亮或灭掉,满足上述要求的电路应是如图9所示的
10.水中气泡看起来比较亮,对这一现象有以下不同的解释,其中正确的是
A.空气泡对光线有会聚作用,因而较亮 B.空气泡对光线有发散作用,因而较亮
C.从水中到达空气泡的界面处的光一部分发生全反射,因而较亮
D.从空气泡到达水中的界面处的光一部分发生全反射,因而较亮
二、填空题
11.如图11所示,在地面上方有一个匀强电场,在该电场中取一点O作为圆心,以R=10 cm为半径,在竖直平面内做一个圆,圆平面平行于匀强电场的电场线,在O点固定一个电量为Q=-5×10-4 C的电荷,当把一个质量为m=9 g,电量为q=2×10-10 C带电小球放在圆周的a点时,它恰好能静止不动,那么匀强电场的电场线跟oa线夹角为 .若将带电小球从a点缓慢移到圆周上最高点b,外力做功W= J.

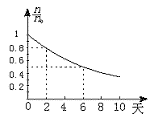
图11 图12
12.如图12所示,通过实验得到某种放射性元素的衰变规律(纵坐标n/n0表示的是任意时刻放射性元素的原子数与t=0时的该原子数之比),该放射性元素的半衰期是 天.在从某古迹中发掘出来的木材中,所含![]() C的比例是正在生长的植物中的80%,放射性
C的比例是正在生长的植物中的80%,放射性![]() C的半衰期是5700年,根据图象可以推算,该古迹距今约
年.
C的半衰期是5700年,根据图象可以推算,该古迹距今约
年.
三、计算题
13.如图13所示的是示波管的示意图.水平x和竖直y偏转电极的板长都为l=4 cm,电极间距离都为d=1 cm,板右端到荧光屏L=18 cm,电子沿中心轴线进入偏转电极时的速度为v0=1.6×107 m/s,基本电荷e=1.6×10-19 C,质量为0.91×10-30 kg.求:
(1)为使电子束不会打在偏转电极的极板上,加在偏转电极上的电压不能超过多少?
(2)若在偏转电极上加某一频率为50 Hz的正弦交变电压时,观察到荧光屏上的竖直亮线长4 cm,试写出该交变电压的表达式.
(3)若在水平方向(x)加上恒定电压Ux(小于最大偏转电压),在竖直方向加Uy=Uysin100πt(小于最大偏转电压),画出荧光屏上亮线大致的形状.
(4)若在水平方向(x)加Ux=Ucos100πt(小于最大偏转电压),在竖直方向(y)加Uy=Usin100πt(小于最大偏转电压),画出荧光屏上亮线大致的形状.
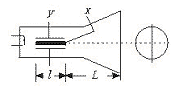
图13
14.太阳与地球的距离为1.5×1011 m,太阳光以平行光束入射到地面.地球表面2/3的面积被水面所覆盖,太阳在一年中辐射到地球表面水面部分的总能量W约为1.87×1024 J.设水面对太阳辐射的平均反射率为7%,而且将吸收到的35%能量重新辐射出去.太阳辐射可将水面的水蒸发(设在常温、常压下蒸发1 kg水需要2.2×106 J的能量),而后凝结成雨滴降落到地面.
(1)太阳辐射到地球的能量中只有约50%到达地面,W只是其中的一部分.太阳辐射到地球的能量没能全部到达地面,这是为什么?请说明二个理由.
(2)估算整个地球表面的年平均降雨量(以毫米表示,球面积为4πR2,已知地球半径为6.37×106 m).
15.讨论有关简谐运动的问题:
(1)用简明的语言表述简谐振动的定义.
(2)如图15所示,一根劲度系数为k的轻质弹簧上端固定在A点,下端挂一质量为m的金属小球,系统静止时金属小球球心位置为O,现用力向下拉小球到B点,待稳定后由静止释放小球,以后小球在BOC之间上下往复运动过程中弹簧处在弹性限度内,不计空气阻力和摩擦.试论述小球在BOC之间的往复运动属于简谐振动.
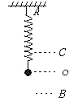
![]()
图15 图16
16.如图16所示, 长木板A右边固定着一个挡板, 包括挡板在内的总质量为1.5M, 静止在光滑的水平地面上.小木块B质量为M, 从A的左端开始以初速度v0在A上滑动, 滑到右端与挡板发生碰撞,已知碰撞过程时间极短, 碰后木块B恰好滑到A的左端就停止滑动.已知B与A间的动摩擦因数为μ, B在A板上单程滑行长度为l.求:
(1)若μl=![]() , 在B与挡板碰撞后的运动过程中, 摩擦力对木板A做正功还是负功?做多少功?
, 在B与挡板碰撞后的运动过程中, 摩擦力对木板A做正功还是负功?做多少功?
(2)讨论A和B在整个运动过程中, 是否有可能在某一段时间里运动方向是向左的.如果不可能, 说明理由; 如果可能, 求出发生这种情况的条件.
高三物理模拟(六)答案
一、单项选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | B | D | C | A | A | D | B | D | C |
二、填空题
11. 45°,9×10-3
12. 6 1900
三、计算题
13. (1)![]() L=v0t U=91
V
L=v0t U=91
V
 (2)U=36sin314t V
(2)U=36sin314t V
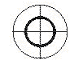
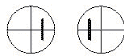
(3)如图所示的左图或中图
(4)如图所示的右图
14. (1)大气层的吸收、散射式反射、云层遮挡等.
(2)设水面所能吸收的能量W′为:
W′=W×(1-7%)×(1-35%)=1.13×1024 J
则凝结成雨滴降到地面水的质量m为:
m=W′/W=5.14×1017 kg
则地球表面年平均降雨量h为:
h=![]() =
=![]() mm=1.01×103 mm
mm=1.01×103 mm
15. ![]() (1)物体在跟位移的大小成正比,并且总是指向平衡位置的力作用下的振动叫简谐振动.
(1)物体在跟位移的大小成正比,并且总是指向平衡位置的力作用下的振动叫简谐振动.
(2)设小球运动中受到竖直向下的力为正,竖直向上的力为负,O是它的平衡位置,ΔL是小球在O点弹簧的伸长量.
在O点时,F合=mg-kΔL=0解出mg=kΔL
以O点为原点建立如图坐标系Ox,方向向下
设小球在BOC之间运动的任意时刻的位移为x,
该点小球受的力为:mg和-k(x+ΔL)
F合=mg-kΔL=-kx
式中“-”表示力的方向与位移方向相反.由于x是任意时刻的位移,所以它在任意时刻的回复力都跟位移x的大小成正比且方向总指向平衡位置.
16.解: (1)B与A碰撞后, B相对于A向左运动, A受摩擦力向左, A的运动方向向右, 故摩擦力做负功.
设B与A碰撞后的瞬间A的速度为v1,B的速度为v2.A、B相对静止后的共同速度为v.整个过程中A、B组成的系统动量守恒,
Mv0= (M + 1.5M)v
v=![]()
碰撞后直至相对静止的过程中, 系统动量守恒, 机械能的减少量等于系统克服摩擦力做的功, 即
Mv2+ 1.5Mv1= 2.5Mv ①
![]() ×2.5Mv2=Mμgl ②
×2.5Mv2=Mμgl ②
可解出v1=![]() (另一解v1=
(另一解v1=![]() v0因小于v而舍去)
v0因小于v而舍去)
这段过程中, A克服摩擦力做功
W=![]() ×1.5Mv12-
×1.5Mv12-![]() ×1.5Mv2
×1.5Mv2
=![]() Mv02(0.068Mv02)
Mv02(0.068Mv02)
(2)A在运动过程中不可能向左运动, 因为在B未与A碰撞之前, A受到的摩擦力方向向右, 做加速运动, 碰撞之后A受到的摩擦力方向向左, 做减速运动, 直到最后, 速度仍向右, 因此不可能向左运动.
B在碰撞之后, 有可能向左运动, 即v2< 0.
先计算当v2= 0时满足的条件, 由①式,
v1=![]() , 当v2= 0时, v1=
, 当v2= 0时, v1=![]() .
.
代入②式,
得![]() ×1.5M
×1.5M![]() =Mμgl,解出μgl=
=Mμgl,解出μgl=![]()
B在某段时间内向左运动的条件是μl<![]()
有什么问题请来信至: mailto: