高三物理公式证明题总复习
[内容精讲] 在高考物理考试说明的题型示例中，出现了公式证明题。在解这类问题时，要有一定的文字说明，首先必须交待所用的每个物理量的含义，其次要分析过程，并说明所用的物理概念或规律。下面给出的是高中物理公式证明题总复习的示例。
一．证明运动学中的几个推论
设物体做匀变速运动，初速度为v0，末速度为vt，加速度为a，运动时间为t，中间时刻的速度为vt/2，中间位置的速度为vs/2，证明：
1．
2.
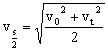
3.vt2-vo2=2as
4.Δs=aT2
[证明]1．根据运动学公式：vt=vo+at, s=vot+at2/2,
中间时刻的速度：vt/2=vo+at/2
平均速度：
又(v0+vt)/2=(v0+v0+ at)/2= vo+at/2,
所以
2．vt2-vo2=2as……（1） vs/22-vo2=2a(s/2)……（2)
(1)/(2):vs/22=(vo2+vt2)/2,
所以有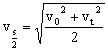
3.根据vt=vo+at, 得：t=(vt-vo)/a,把t代入
s=vot+at2/2, 得：vt2-vo2=2as
4.从第一个T秒开始时计时，在该时刻t=0,速度为v0，有：
s1=v0T+aT2/2, s2=（v0+aT）T+aT2/2, s3=（v0+2aT）T+aT2/2,……
sn=[v0+（n-1）aT]T+aT2/2,
s2 -s1= s3 –s2=……=Δs=aT2
二．证明动能定理：外力对物体所做的总功等于物体动能的增加．
证明：一个质量为m的物体原来的速度为v1，动能为m v12/2，在恒力F的作用下，发生一段位移s，速度为v2，动能增加到m v22/2，设外力方向与运动方向相同，外力F做的功W=Fs，根据牛顿第二定律F=ma，由运动学公式v22-v12=2as,得：s= (v22-v12)/2a,所以
Fs=ma(v22-v12)/2a= m v22/2- m v12/2
或W=EK2- EK1
上述结论由假定物体受一个力推导出来的，如果不只受一个力而是几个力， 总功就是各个力做功的代数和．
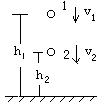三．证明机械能守恒定律：在只有重力做功的情形下，物体的动能和重力势能发生相互转化，但总的机械能保持不变．
证明：如图所示，取地为零势能点，设物体只受重力作用，向下做匀加速运动。在位置1时速度为v1，高度为h1，在位置2时速度为v2，高度为h2，由匀加速运动公式可得：v22-v12=2g(h1-h2)
v12+2gh1= v22+2gh2 ,
mv12/2+mgh1=m v22/2+mgh2
即，E1=E2
所以机械能守恒．
四．求证在串联电路中：1．串联电路的总电阻，等于各导体的电阻之和．2．串联电路中各个电阻两端的电压跟它的阻值成正比．3．串联电路中各个电阻消耗的功率跟它的阻值成正比．
证明：1．根据流过串联电路各电阻的电流相等和串联电路两端的总电压等于各部分电路两端的电压之和，可得：
I=I1=I2=……=In …………（1）
U=U1+U2+……+Un …………（2）
根据欧姆定律：U=IR，U1=IR1, U2=IR2，…… Un=IRn， …………（3）
把上述关系式代入（2）式，整理后可得：R=R1+R2+……+Rn
2．由欧姆定律，将（3）式改写成
I=U/R,I1=U1/R1,I2=U2/R2, ……，In=Un/Rn，代入（1）式得：
U1/R1=U2/R2……=Un/Rn =I，所以U∝R
3．由功率公式 :
P1=I12R1, P2=I22R2……， Pn=In2Rn，代入（1）式得：
P1/R1=P2/R2=……Pn/Rn=I2，所以P∝R
五．求证在并联电路中：1．并联电路总电阻的倒数，等于各个导体的电阻倒数之和．2．并联电路中通过各导体的电流跟它的电阻成反比．3．并联电路中各个电阻消耗的功率跟它的阻值成反比．
证明：1．根据并联电路中各支路两端的电压相等和并联电路中的总电流等于各支路电流之和，可得：
U=U1=U2=……=Un …………（1）
I=I1+I2+……+In …………（2）
由欧姆定律，I=U/R,I1=U1/R1,I2=U2/R2, ……，In=Un/Rn，代入（2）式并考虑到（1）式，得：
1/R=1/R1+1/R2+……1/Rn
2.在并联电路中，根据欧姆定律：
U=IR，U1=I1R1, U2=I2R2，…… Un=InRn， …………（3）
代入（1）式得：
I1R1=I2R2，…… =InRn =U所以I∝1/R
3．由功率公式：P1=U12/R，P2=U22/R，……Pn=Un2/R，即：
U12=P1R，U22=P2R，……Un2=PnR，将其代入（1）式并平方，得：
P1R=P2R=……PnR= U2，所以P∝1/R
六．求证：电流与自由电子定向移动速率的关系式I=neSv．
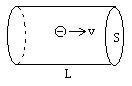证明：如图所示,设对一段导线通以强度为I的电流，导线截面积为S，电子定向移动速率为v，单位体积内电子数为n，通电时间为t.
则在这段时间内，电子定向移动的距离为L=vt,
通过导线截面的电量为q=enV=enSL=neSvt.
所以电流为I=q/t=neSv．
七．证明：洛仑兹力公式f=qvB.
证明：设导线中单位体积内含有的运动电荷数是n，每个电荷的电量是q，电荷的平均定向移动速率是v，导线的横截面积是S，那么通过导线的电流就是
I=nqvS
磁场对电流的作用力是F=ILB．这个力可看作是作用在每个运动电荷上的洛仑兹力的合力，设洛仑兹力为f，这段导线内运动电荷的总数为N，则
Nf=F，即Nf=ILB,
代入I=nqvS，得到Nf=nqvSLB
又N等于单位体积内的运动电荷数跟体积的乘积，即N=nSL，因此上式简化为
f=qvB
八．求证：半径公式r=mv/Bq，周期公式T=2πm/Bq
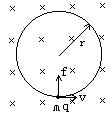证明：如图所示，设一带电粒子质量为m，带电量为q，匀强磁场的磁感强度为B，粒子做匀速圆周运动的向心力为洛仑兹力，即
Fn=qvB=mv2/r
所以运动半径为r=mv/Bq．
根据周期公式T=2πr/v,将r=mv/Bq代入得
带电粒子的运动周期为T=2πm/Bq．
九．证明：导体切割磁感线产生的电动势ε=BLv.
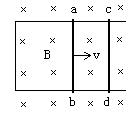证明：如图所示，假设垂直水平轨道放置的导体棒长L，以速度v在轨道上向右运动，设在Δt时间内棒由原来的位置ab移到cd，这时线框的面积变化量ΔS=LvΔt，
穿过闭合电路的磁通量变化量ΔΦ=BΔS=BLvΔt，
由法拉第电磁感应定律ε=ΔΦ/Δt,将上式代入得
导体切割磁感线产生的电动势ε=BLv．
十．证明：交流电动势公式ε=nBSωsinωt.（从中性面计时）
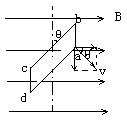
证明：如图所示，设线圈从中性面开始转动，角速度是ω，经时间t，线圈转过的角度为ωt，ab边线速度的方向跟磁感线方向的夹角也为θ=ωt，设磁感强度为B，线圈面积为S，ab边、cd边的感应电动势为
εab=εcd=B·ab·vsinωt= B·ab·(bc/2) ωsinωt=BSωsinωt/2
并且两者串联，所以线圈中的电动势为ε=BSωsinωt.
若线圈有n匝，则电动势为ε=nBSωsinωt.
[课外作业]
1．证明动量定理。
2．试用万有引力定律证明：对于某个行星的所有卫星来说，R3/T2是一个恒量。其中R是卫星的轨道半径，T是卫星的运行周期。
3．行星的密度是ρ，靠近得星表面的卫星运动周期是T。试证明ρT2是一个普遍适用的恒量，即它对任何行星都相同。