高三物理第二轮综合复习牛顿运动定律
基础过关检测试题一
一、单项选择题:每题6分、共48分
1.做平抛运动的物体,每秒的速度增量是( )
A.大小相等,方向相同 B.大小相等,方向不同
C.大小不等,方向相同 D.大小不等,方向不同
2.下面关于匀速圆周运动的说法正确的是( )
A.匀速圆周运动是一种平衡状态
B.匀速圆周运动是一种匀速运动
C.匀速圆周运动是一种匀变速运动
D.匀速圆周运动是一种速度和加速度都不断改变的运动
3.以速度V0水平抛出一小球,如果从抛出到某时刻小球的竖直分位移与水平分位移大小相等,以下判断正确的是 ( )
A.此时小球的竖直分速度大小等于水平分速度大小
B.此时小球的速度大小为![]() V0
V0
C.小球运动的时间为![]()
D.此时小球速度的方向与位移的方向相同
4.关于作用力与反作用力以及相互平衡的两个力的下列说法中正确的是 ( )
①作用力与反作用力是同一性质的力
②作用力与反作用力大小相等,方向相反,因而可以相互抵消
③相互平衡的两个力性质可以相同,也可以不同
④相互平衡的两个力大小相等,方向相反,同时出现,同时消失
A.①② B.②③ C、①④ D.①③ :
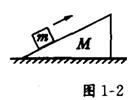 5.如图1—2所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中 ( )
5.如图1—2所示,斜劈形物体的质量M,放在水平地面上,质量为m的粗糙物块以某一初速沿斜劈的斜面向上滑,至速度为零后又加速返回,而斜劈始终保持静止,物块m上、下滑动的整个过程中 ( )
①地面对斜劈M的摩擦力方向先向左后向右
②地面对斜劈M的摩擦力方向没有改变
③地面对斜劈M的支持力总小于(M+m)g
④物块m上、下滑动时的加速度大小相同
A.①③ B、①④
 C.②③ D.②④
C.②③ D.②④
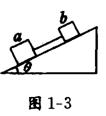
6,如图1—3所示,两个物体d、占的质量满足:ma=2mb,用细绳连接后放在倾角为θ的光滑斜面上,在下滑的过程中 ( )
①它们的加速度为a=gsinθ
②它们的加速度为a<gsinθ
③细绳的张力为零
④细绳的张力为mgsinθ
A.①⑧ B.①④ C.②③ D.②④
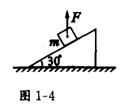 7.如图1—4所示,一个质量为m=2.0kg的物体,放在倾角为θ=300的斜面上静止不动.若用竖直向上的力F=5.0N提物体,物体仍静止(g=10m/s2),则下述结论正确的是 ( )
7.如图1—4所示,一个质量为m=2.0kg的物体,放在倾角为θ=300的斜面上静止不动.若用竖直向上的力F=5.0N提物体,物体仍静止(g=10m/s2),则下述结论正确的是 ( )
A. 物体受到的合外力减少5.0N
B,物体受到的摩擦力减少5.0N
C.斜面受到的压力减少5.0N
 D.物体对斜面的作用力减少5.0N
D.物体对斜面的作用力减少5.0N
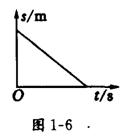
8.物体在粗糙的水平面上运动,其s-t图象如图l—6所示,已知沿运动方向的作用力为F,所受的滑动摩擦力为f,则由图可知 ( )
A.F>f B.F=f
 C.F<f D.以上三种情况都有可能
C.F<f D.以上三种情况都有可能
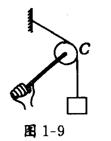
9.手握轻杆,杆的另一端安装有一个小滑轮C,支持着悬挂重物的绳子,如图1—9所示.现保持滑轮C的位置不变,使杆向下转动一个角度,则杆对滑轮C的作用力将( )
A.变大 B.不变
C.变小 D.无法确定
二、计算论述题:
10.雨滴从高空竖直落到地面的过程中,由于空气阻力的作用,雨滴在下落一段距离后就做匀速运动.已知空气阻力f=kSv2,其中,是雨滴的下落速度,S是雨滴的横截面积,k是常数.将雨滴看做是球形,试导出雨滴落地速度大小与雨滴半径的关系式,说明什么样的雨滴落地时速度较大.
11.羚羊从静止开始奔跑,经过50m的距离能加速到最大速度为25m/s,并能维持一段较长时间,猎豹从静止开始奔跑,经过60m的距离能加速到最大速度为30m/s,以后只能维持此速度4.0s.设猎豹距离羚羊x时开始攻击,羚羊则在猎豹开始攻击后1.0s才开始奔跑.假设羚羊和猎豹在加速阶段分别做匀加速运动,且均沿同一直线奔跑,则
(1)猎豹要在其加速阶段追到羚羊,x值应在什么范围?
(2)猎豹要在最大速度减速前追到羚羊,x值应在什么范围?
12.一个质量为4kg的物体,放在动摩擦因数为0.1的水平面上,开始时处于静止状态.先给它施加一个水平向西的12N的力F1,作用2s后,撤去这个力,同时给它一个水平向东的大小为12N的力F2,又作用2s后再撤去这个力.求这个物体在这4s内通过的位移与它在第4s末的速度,
13.一辆汽车通过某一拱形桥顶点时的速度大小为36 km/h,汽车对桥顶的压力为车重的3/4,如果要使汽车在桥顶对桥面没有压力,汽车过桥时的速度至少应为多大?(g取10m/s2)
参考答案
一、选择题:
1A、2D、3C、4D、5C、6A、7D、8B、9B
二、计算论述题:
10、解:设雨滴的形状为球形,其半径为R,横截面积为S,体积为V,则:
V=![]() πr3=
πr3=![]() SR
SR
雨滴落地时已做匀速运动,设其质量为m,则
mg-KSv2=0
设雨滴的密度为ρ,则:m=ρV
解以上三式得:v=![]()
由此可知:v∝![]() ,所以,雨滴越大(
,所以,雨滴越大(![]() 越大),其落地时的速度越大。
越大),其落地时的速度越大。
11、解:⑴根据题意,猎豹奔跑时的加速度为:
a1=![]() =
=![]() m/s2=7.5m/s2
m/s2=7.5m/s2
猎豹的加速时间为:t1=![]() =
=![]() s=4s
s=4s
羚羊奔跑时的加速度为:a2=![]() =
=![]() m/s2=6.25m/s2
m/s2=6.25m/s2
羚羊加速的时间为:t2=![]() =
=![]() s=4s
s=4s
由于羚羊晚跑1s,所以猎豹在加速阶段追到羚羊,x值的范围应为:
x≤![]()
⑵根据题意,猎豹以最大的速度且在极限时间内奔跑的距离是:30m/s×4s=120m,猎豹一共奔跑的距离为:s=60m+120m=180m
羚羊在猎豹开始攻击1.0s后才开始奔跑,设羚羊以最大速度奔跑了3s,羚羊以最大速度奔跑的距离为:25m/s×3s=75m,羚羊一共奔跑的距离为:
s′=50m+75m=125m
猎豹攻击羚羊的距离范围为:x≤180m—125m=55m。
12、解:设向西为正,则:
a1=![]() =2m/s2
=2m/s2
v1=a1t1=4m/s
s1=![]() a1t12=4m
a1t12=4m
a2=—![]() =—4m/s2
=—4m/s2
v2=v1+a2t2=4—4t2
当t2=1s时,v2=0
s2=![]() =2m
=2m
接下来的t3=1s内,有:a3=—![]() =—2m/s2
=—2m/s2
故第4s末的速度为:v3=a3t3=—2m/s,(方向向东)
s3=![]() =—1m,(方向向东)
=—1m,(方向向东)
4s内通过的位移为:s=s1+s2+s3=(4+2—1)m=5m
13、解:汽车以v1=36km/h=10m/s的速度通过拱形桥顶点时,有:
mg—![]() mg=m
mg=m![]() ,
,
设汽车过桥速度为v2时对桥面没有压力,则:
mg=m![]()
解之得:v2=2v1=20m/s=72km/h