高三物理寒假力学综合练习

北　京　四　中

年　　级：高　三　 　　科　　目：物　理　　期　数：0121

编稿老师：李建宁　　　 审稿老师：李建宁　　录　入：申容

校　　对：刘红梅

高三物理寒假力学综合练习

一、选择题：

1、有两颗人造地球卫星A、B，它们的轨道半径分别为r_A和r_B，且r_A<r_B。设它们的速度大小分别为v_A和v_B，它们的周期分别为T_A和T_B，则有：

A、v_A>v_B　T_A>T_B　 B、v_A>v_B　T_A<T_B

C、v_A<v_B　T_A>T_B　 D、v_A<v_B　T_A<T_B

2、一个物体在多个力作用下处于静止状态，如果仅使其中一个力的大小逐渐减小到零，然后逐渐从零恢复到原来的大小，而保持其方向不变，则下列图中能够正确描述物体的速度随时间变化情况的是：

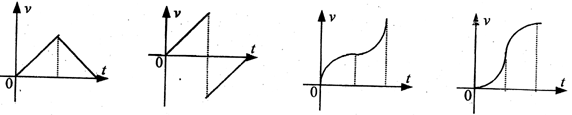
　　　A、　　　　  B、　　　　　　  C、　　　　 D、

3、关于摩擦力做功的问题，以下说法正确的是（　　）

A、滑动摩擦力总是做负功

B、滑动摩擦力既可能做正功，也可能做负功

C、静摩擦力对物体总是做正功

D、一对相互作用的静摩擦力做功之和为相对静止的两个运动物体产生的热能之和

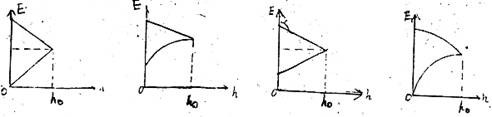4、将一个物体竖直上抛，上抛运动过程中所受到的空气阻力大小恒定，若以地面为零势能参考面则在物体从抛出至落地的过程中，物体机械能与物体距地面高度的图象是（如图IV·4——2中h_o为上抛的最大高度）（　　）

　　　　A、　　　　B、　　　　　  C、　　　　D、

5、如图所示，一物块以6米/秒初速度从曲面A点下滑，运动到达B点速度仍为6米/秒，若物块以5米/秒的初速度仍由A点下滑，则运动到B点时的速度

A、等于5米/秒；

B、大于5米/秒；

C、小于5米/秒；

D、条件不足，无法判断。

6、做简谐振动的弹簧振子如图所示，其振子的质量为m，振动过程中最大速率为V，从某一时刻算起，在半个周期内（　　）

A、弹力做的功一定为零　

B、弹力做的功可能是零到mv²之间的某一值

C、弹力的冲量一定为零

D、弹簧和振子系统的机械能和动量都守恒

7、以初速度10米/秒从地面竖直向上抛一物体，空气阻力是物体重力的0.2倍，g取10米/秒²，当物体动能与重力势能相等时，物体离地面的高度是（　　）

A、1.85米　　B、2.5米　C、2.27米 D、3.7米

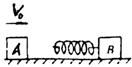8、如图所示，光滑水平面上有A、B两个物体，其中带有轻弹簧的物体B静止，质量为m的物体A以速度v₀向着B运动，在A通过弹簧与B发生相互作用的过程中：

A、弹簧恢复原长时，A的速度一定最小；

B、两物体速度相等时弹簧的压缩量最大；

C、任意时刻A的动量总小于mv₀；

D、任意时刻系统的总动量均为mv₀；

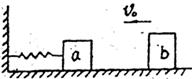9、如图所示，在光滑水平面上，有a、b两物体，质量分别为m_a=3m, m_b=m, a与轻弹簧相连，弹簧的另一端固定在墙上，弹簧无形变。b物体以V₀的速度与a物体发生正碰，碰后两物体以相同的速度一起运动并压缩弹簧，当弹簧被压缩到最短时，具有的弹性势能为（　　）

A、mV₀²　 B、mV₀²　 C、mV₀²　 D、mV₀²

10、如图所示，为波沿着一条右端固定的绳子传播到B点的波形示意图，由图可判断出A开始振动的方向是：（　　）

A、向左　B、向右　C、向上　D、向下

11、质量相等的A、B、C三个小球，从同一高处抛出，A球竖直上抛、B球竖直下抛，C球水平抛出，下列叙述正确的是：（　　）

A、着地前，在相等时间内三球动量变化量相等

B、着地时，三个小球的动能相等

C、着地时，三球动量相等

D、从抛出到着地的过程中重力对A球做功的平均功率最小

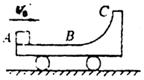12、如图所示，质量为M的小车静止在光滑水平面上，车上AB段是水平、粗糙的直线轨道，而BC段是光滑的1/4圆弧轨道，现有质量为m的小滑块以水平速度v₀冲上小车，则滑块从AÕBÕCÕBÕA的过程中，

A、滑块与小车组成的系统动量始终守恒；

B、摩擦力对滑块所做的功为零；

C、滑块到达C点时，小车的速度最大；

D、滑块从C返回到B点时，小车的速度最大；

二、填空题：

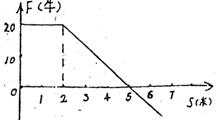
13、某物体在合外力F作用下作初速度为零的加速直线运动，F随位移S变化的图象如图所示。可以看出，在位移为________米处，物体的动能最大。最大的动能是________焦耳。

14、质量为5吨的载重汽车的额定功率为1´10⁵瓦，在平直公路上行驶时受到的阻力为1´10³牛，若载重汽车保持5´10³中的牵引力行驶，则至多只能维持________秒。

15、一质点在O点附近作简谐振动，它离开O点向M点运动，2秒后第一次到达M点，再经过2秒后，第二次到达M点，则再经过________秒后，它将第三次到达M点，这个质点的振动频率为________赫。

16、一个物体受到n个外力作用而处于平衡状态，其中一个力的大小为F₁=4N，方向向右。若其外力都保持不变，只将F₁的方向改变90⁰，大小变为3N，那么，该物体所受合外力的大小是________，方向与第二次的拉力F₁成________角。

17、如图所示，一个质量为M的物体放在水平面上，物体上安装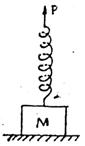了一个长度为L、倔强系数为K的轻弹簧，现用手拉着弹簧上端的P点缓慢向上移动，直到物体离开地面一段距离，在这一过程中，P点的位移是H（开始时弹簧为原长），则物体的重力势能增加量是_______。

18、从地面竖直向上发射一枚礼花弹，当其上升速度为30米/秒时，距地面高度为125米，恰好此时礼花弹炸开，分裂为质量相等的两部分（火药质量损失不计），其中一部分经5秒钟落回发射点，则另一部分的速度大小是_______米/秒，方向是_______。（不计空气阻力，取g=10米/秒）

19、一质量为M的小车，在光滑水平面上以速度V前进，另一质量为m的物体从h高处自由下落到小车上，并与小车共同运动，小车速度为_______；若此物体又从小车上的小孔中落下，这时小车的速度为_______。

20、在光滑水平面上有一质量900克、边长10厘米的正方形木块，质量为100克、速度为200米/秒的子弹沿水平方向垂直木块表面入射。如果木块固定在水平面上，子弹刚好能穿过木块。如果木块没有固定在水平面上，子弹打进木块的深度为_______厘米，在这过程中产生的热量为_______焦耳。（子弹在木块中所受阻力可认为是一恒量）

三、计算题：

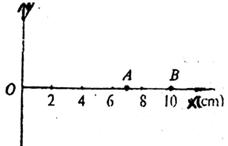21、一列横波沿x轴传播，速度为12米/秒，在x轴上有A、B两点，它们各自的坐标分别为x_A=7厘米，x_B=10厘米，当A点在正的最大位移处时，B点恰在平衡位置且振动方向向下，如图所示 ， 求这列波的频率的表达式和各表达式中的最小频率及与之对应的波长。

22、一条传送带始终水平匀速运动，将一个质量为m=20kg的货物无初速地放到传送带上，货物从放上到跟传送带一起匀速运动，经过的时间是0.8s，滑行距离是1.2m(g=10m/s²)。

求：（1）货物与传送带间动摩擦因数的值

　 （2）这个过程，动力对传送带多做的功是多少？

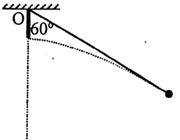23、如图，长为L的不可伸长的轻绳一端系于固定点O，另一端系一质量为m的小球，将小球从O点正下方L处以一定的初速水平向右抛出，经过一段时间绳被拉直，以后小球将以O点为圆心在竖直平面内摆动，已知绳刚被拉直时与竖直方向成60⁰角，求：

　　（1）小球被抛出的初速度

（2）小球将以O点为圆心在竖直平面内摆动的过程中，通过最低点时的速度大小，以及绳子受到的拉力。

24、质量为3吨的汽车，额定功率为80千瓦，汽车在保持额定功率不变的情况下沿水平路面匀速行驶时，能达到的最大速度为72千米/小时，若汽车由静止出发以2米/秒²的加速度匀加速行驶时，汽车匀加速的时间为多少秒，2秒末汽车的即时功率为多少千瓦。（设路面阻力大小不变）

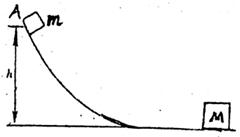25、如图所示，在光滑的曲面AB上有一质量m的小物体，由高为h处从静止滑下它与静止在光滑水平面BC上的质量为M的物体相碰撞，碰后小物体m又返回曲面，然后又从曲面下滑与物体M作第二次碰撞，若两物体是弹性碰撞。问：（1）第一次碰撞后，物体m的速度是多大？（2）要使物体m、M发生第二次碰撞，m与M间应满足何种关系？

26、质量为m的钢板与直立轻弹簧的上端连接，弹簧下端固定在地上，平衡时，弹簧的压缩量为x₀，如图所示，一物块从钢板正上方距离为3x₀的A处自由落下，打在钢板上并立刻与钢板一起向下运动，但不粘连，它们到达最低点后又向上运动，已知物块质量也为m时，它们恰能回到O点，若物块质量为2m, 仍从A处自由落下，则物块与钢板回到O点时，还具有向上的速度，求物块向上运动到达的最高点与O点的距离。

[参考答案]：

一、选择题：

1、B　2、D　3、B　4、C　5、B

6、A　7、AC　8、BCD　9、B　10、D

11、AD　12、D

二、填空题

13、5米　70焦耳

14、25秒

15、10秒　 赫

16、5牛　53⁰

17、mg(H-)

18、60米/秒　竖直向上

19、V　 不变

20、9厘米　1800焦耳

三、计算题

21题：

（1）若波沿x轴正方向传播，则

x_B-x_A=(n+)λ(n=0, 1, 2, 3, ……)

λ=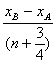(n=0, 1, 2, 3, ……)

f=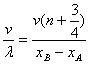(n=0, 1, 2, 3)

最小频率n=0，f_min=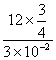=300Hz

最小波长n=0, λ_min=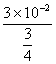=4×10^-2m.

（2）若波沿x轴负方向传播，则

x_B-x_A=(n+)λ(n=0, 1, 2, 3, ……)

λ=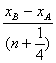(n=0, 1, 2, 3, ……)

f=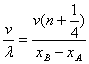(n=0, 1, 2, 3, ……)

最小频率n=0, f_min=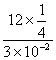=100Hz

最小波长n=0,λ_min=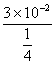=12×10^-2m.

22题：

（1）货物做初速为零的匀加速运动，传送带做匀速运动，设货物相对地位移S₁，相同时间传送带相对地位移S₂，则

S₂-S₁=L，f=N=mg,

S₁=at², a==g

S₂=vt, v=at

代入vt-at²=L

at²-at²=L

gt²=L

==0.375.

（2）动力对传送带做功一部分使货物动能增加；一部分转变成热能fL,

W=mv²+fL=m(at)²+mgL

　=×20×3²+0.375×20×10×1.2

　=180J

23题：

（1）小球在绳被拉直前做平抛运动，

x方向：v₀t=l·sin60⁰,

y方向：l·cos60⁰-=gt²,

l·cos60⁰-=g()²,

v₀=.

（2）确定小球在绳拉直时速度方向，

小球平抛时间：t==,

x方向：v_x=v₀=.

y方向：v_y=gt=g=,

v===.

与竖直之间夹角为，tg==，则=60⁰。

即v与绳同一直线，小球受到外力的冲量动量减为零。以后小球作圆周运动。

根据动能定理，mgl(1-cos60⁰)=mv'²-0.

则v'²=gl,

根据牛顿二定律，设绳拉力为T，

T-mg=m,

T=mg+m=2mg.

24题：

（1）汽车匀速运动时，P₀=Fv_m=fv_m,

则阻力f===4000N,

根据牛顿二定律：（匀加速运动时）

F₁-f=ma,

F₁=f+ma=4000+3000×2=10000N,

汽车匀加最大速度v₁===8m/s,

汽车匀加时间t===4s.

（2）汽车2秒末速度v₂=at₂=2×2=4m/s,

汽车即时功率P'=F₁v₂=40千瓦。

25题：

（1）小物体由光滑曲面下滑机械能守恒，然后与M物体发生弹性碰撞，

mgh=mv₀², （此水平面E_P=0）

v₀=,

m、M、F=0动量守恒，以水平向右为正方向，

mv₀=mv₁+Mv₂ 　v₁=v₀,

mv₀²=mv₁²+Mv₂²　　v₂=v₀

（2）若要使m与M发生第二次碰撞需v₁<0，且v₁>v₂，

-v₀>v₀,

即M>3m.

26题：

（1）钢块自由下落与钢板碰前速度v₀,

v₀²=2g·3x₀，v₀=,

钢块与板碰撞，动量守恒，设碰后速度v₁,

mv₀=(m+m)v₁,　v₁==v₀,

碰后一起下移，再次回到O点过程中机械能守恒。设O点E_P=0，碰时弹簧弹性势能为E_P1，则

E_P1+(m+m)v₁²-2mgx₀=0,

E_P1=2mgx₀-mv₁²=2mgx₀-m×v₀²=mgx₀……(1),

（2）若用2m钢块自由下落与钢板碰撞，动量守恒，设碰后速度为v₂,

2mv₀=(m+2m)v₂,　v₂=v₀,

此刻弹簧弹性势能仍为E_P1，机械能守恒，

E_P1+(3m)v₂²-3mgx₀= (3m)v₃²,

将(1)代入，v₃²=gx₀,

物以v₃上抛h, v₃²=2gh,

则h==x₀.