力学计算题专项测试（二）

力学计算题专项测试（二）

1、  如图所示，质量为M的木块放在水平地面上，一轻质弹簧下端固定在木板上，上端固定一个质量为m的小球，小球上下跳动时，木块始终没有跳起，求在木块对地面压力为零的瞬间，小球的加速度是多大？小球跳动的全过程中木板对地面的最大压力是多少？

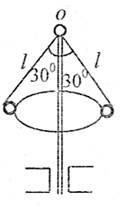2、蒸汽机中自动控制转速的装置叫做离心节速器，它的工作原理和下述力学模型类似：在一根竖直硬质细杆的顶端O用铰链连接两根轻杆，轻杆的下端分别固定两个金属小球。当发动机带动竖直硬质细杆转动时，两个金属球可在水平面上做匀速圆周运动，如图所示。设与金属球连接的两轻杆的长度均为l，两金属球的质量均为m，各杆的质量均可忽略不计。当发动机加速运转时，轻杆与竖直杆的夹角从30°增加到60°，求这一过程中发动机对小球所做的功。忽略各处的摩擦和阻力。

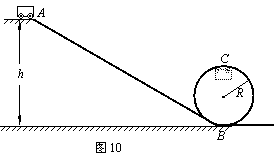3、如图10所示是一个设计“过山车”的试验装置的原理示意图，光滑斜面AB与竖直面内的圆形轨道在B点平滑连接，圆形轨道半径为R。一个质量为m的小车（可视为质点）从距地面h高处的A点由静止释放沿斜面滑下。已知重力加速度为g。

  （1）求当小车进入圆形轨道第一次经过B点时对轨道的压力；　

　（2）假设小车恰能通过最高点C完成圆周运动，求小车从B点运动到C克服摩擦阻力做的功。

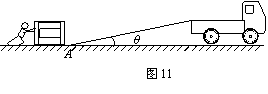4、某人欲将质量m=2.0×10²kg的货箱推上高h=1.0m的卡车，他使用的是一个长L=5.0m的斜面(斜面与水平面平滑连接)，如图11所示。假设货箱与水平面和斜面的动摩擦因数均为μ=0.10，此人沿平行于地面和斜面对货箱所施的最大推力均为F_m=4.0×10²N。（为计算方便可认为cosθ≈1，g=10m/s²）。

（1）从斜面底端用平行于斜面的力把货箱匀速推上卡车，需多大的推力？

（2）若货箱在水平面和斜面上时，人对货箱所施加的推力F_m分别平行与水平面和斜面，那么，为把静止在水平地面上的货箱推到斜面顶端的卡车上，需从距A点至少多远的地方推动货箱？

（3）通过推导说明，用最大推力为F_m将货箱推上卡车时做功最少。

答案：1、解：当木块对地压力为零时，弹簧对m有向下的拉力为Mg，分析m受力由牛顿第二定律有Mg+mg=ma　…………2分　　  得　………………2分

　  在最低点小球的加速度和最高点的加速度相同　…………2分

　  分析m有　　……2分　　分析M有　…2分

2、解：设小球在偏角为30°和60°做匀速圆周运动的速度大小分别为v₁和v₂，

　  上升的高度为h，根据牛顿第二定律有　 …………2分

　  　 …………2分　　上升的距离　 　…………2分

根据动能定理得　　　由以上方程解得　　……2分

3、（1）N= （2）W_f=mg

4、1）ΔF= 600N(或596N)　（2）5.0m（或s=4.9m）

（3）设此人沿水平方向和沿斜面方向推力均为F，在水平面上移动的距离为s，滑动摩擦力为f₁,在斜面上的滑动摩擦力为f₂，把货箱推到卡车上时货箱的速度恰好为零，根据动能定理F(s+L)-f₁s-f₂L-mgLsinθ=0，则F=μmg+,

　 解得W_F= F(s+L)= μmgs+μmgLcosθ+mgLsinθ，因为μ、m、g、h、L都是定值，

　　推力做功的大小取决于s大小，s大时，F则小。所以，F_m最大时，s最少，W_F最少。