力学计算题专项测试（三）
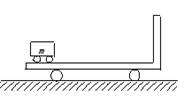1、如图所示,质量为M=20 kg的平板车静止在光滑的水平面上;车上最左端停放着质量为m=5kg的电动车,电动车与平板车上的挡板相距L=5 m.电动车由静止开始向右做匀加速运动,经时间t=2s电动车与挡板相碰,问:
(1) 碰撞前瞬间两车的速度大小各为多少?
(2) 若碰撞过程中无机械能损失,且碰后电动机关闭并刹车,使电动车只能在平板车上滑动,要使电动车不脱离平板车,它们之间的动摩擦因数至少多大?
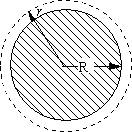
2、设想宇航员完成了对火星表面的科学考察任务，乘坐返回舱返回围绕火星做圆周运动的轨道舱，如图所示。为了安全，返回舱与轨道舱对接时，必须具有相同的速度。已知返回舱返回过程中需克服火星的引力做功
，返回舱与人的总质量为m，火星表面的重力加速度为g ，火星的半径为R，轨道舱到火星中心的距离为r，不计火星表面大气对返回舱的阻力和火星自转的影响，则该宇航员乘坐的返回舱至少需要获得多少能量才能返回轨道舱？
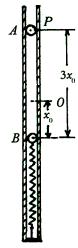3、质量为m的小球B用一根轻质弹簧连接．现把它们放置在竖直固定的内壁光滑的直圆筒内，平衡时弹簧的压缩量为
，如图所示，小球A从小球B的正上方距离为3x0的P处自由落下，落在小球B上立刻与小球B粘连在一起向下运动，它们到达最低点后又向上运动，并恰能回到0点(设两个小球直径相等，且远小于略小于直圆筒内径)，已知弹簧的弹性势能为
，其中k为弹簧的劲度系数，Δx为弹簧的形变量。求：
(1)小球A质量。
（2）小球A与小球B一起向下运动时速度的最大值．
答案：1、(1)设两车从静止到碰撞前瞬间,平板车相对地发生的位移为x,则电动车相对地发生的位移为L-x.
由动量守恒定律,有:m-M=0
解得x=1 m
设碰前电动车、平板车的速度分别为V1、V2,因两车在碰前均做初速度为零的匀加速直线运动,由平均速度公式:V——==
V1=2×=…=4m/s
V2=2×=…=1m/s
(2) 因碰撞过程中系统动量守恒且无机械能损失,说明两车碰后分别以原速度大小沿相反方向运动
欲使电动车不脱离平板车,由能量守恒定律可知:
mV12+MV22≤µmgL
代入已知数据,可得:µ≥0.2
2、.解：返回舱与人在火星表面附近有：
（2分）
设轨道舱的质量为m0，速度大小为v，则：
（2分）
解得宇航员乘坐返回舱与轨道舱对接时，具有的动能为
（2分）
因为返回舱返回过程克服引力做功
所以返回舱返回时至少需要能量
（4分）
3、解：（1）由平衡条件可知：mg=kx0 （1分）
设A的质量为m'，A由静止下落后与B接触前的瞬时速度为v1，则：
（2分）
设A与B碰撞后的速度为v1'，有：
（2分）
由于A、B恰能回到O点，据动能定理有：
解得：m'=m （3分）
（2）设由B点再向下运动x1时，它们的速度达到最大，此时它们的加速度为零，有：
（2分）
据机械能守恒定律有：
（2分）
解得：
（1分）