高三物理学科内综合
物理学科内综合测试题以物理学科基本知识、基本方法、各部分知识内容间综合知识为考查内容，强调物理理论和实际相结合，学以致用，不再局限在将科学方法应用于处理物理问题、推测答案，仅仅考查学生的归纳、演绎、推理等思维能力的环节上，而是全面考查学生观察能力、发现问题和提出问题的能力、自学能力、知识迁移能力，特别是创造性思维能力。它反映了以创新精神和实践能力为核心的素质教育的要求。因此，在物理学科的学习中，必须注重综合能力的培养。
(一)在知识形成的过程中培养综合能力
知识是形成能力的基础，没有知识根本谈不上能力。但知识的获得不能只靠记忆、背诵一些现成的结论，要注意知识形成的过程，在过程中渗透物理思想和物理方法。对于概念、规律，要知道其发展的来龙去脉，不但要知其然，更要知其所以然。如对于一个概念，要弄清楚问题怎样提出的，为什么要引入这个概念，怎样引入，它的定义是什么，内涵和外延是什么，它与其相近和有关联的概念的联系和区别是什么，与相关联的物理量形成什么规律，这些规律的适用条件是什么，如何应用这些规律，等等。这样的知识不是靠死记硬背，而是建立在理解基础之上的，只有这样，才能更深刻的把握和灵活的运用，才能形成物理能力，从而发展综合能力。
(二)在构建物理知识和方法的结构体系中培养综合能力
物理学研究的是物质世界最基本、最普遍的运动形态和规律。因此，物理知识之间的逻辑关系也最为明显和清晰，能形成非常严密的结构体系。知识形成体系，知识在体系中的位置、地位以及与其它知识的联系才能明显的暴露出来，便于同学理解、掌握，有利于知识的存储、记忆和提取。特别是对综合能力的培养，在很大程度上依赖于学生认知结构体系建立的好坏。经常有这样的情况，有些同学在物理课上觉得都听懂了，都明白了，但就是不会做题，复习的时候也觉得知识都掌握了，但就是不会应用，更不会解综合性的问题。原因就在于他的知识是无序的，知识点彼此孤立，形不成结构，不知道知识之间的内在联系，无法综合。
我们的同学在平时的学习中和复习中，一定要有意识地去认识和构建知识的结构体系。知识点要形成线，线要形成面，面要形成网络。这种有层次的网络化了的结构体系，能发挥巨大的功能。首先，能了解哪些知识是普遍适用的，哪些知识是在一定条件下才适用的，它的适用条件是什么，从而明确各种知识解决具体问题所能达到的程度。其次，有助于认识知识之间的内在联系和深刻本质，有助于进一步产生丰富的联想，形成综合能力。构建结构体系的形式和方法多种多样，可以是一章的，也可以是某一部分的，还可以是某一个专题的。
知识能形成结构，物理方法同样也能形成结构。物理方法是形成知识和应用知识解决问题的途径，对形成综合能力来说方法比知识更重要。我们在学习中要不断总结物理方法，同样形成体系。明确哪些是一般的普遍适用的方法，哪些是特殊的方法，什么情况下才能使用，如何运用它们。如，研究力学问题的方法是：确立研究对象，分析受力，确定运动状态，列方程解方程。研究热学问题的方法是：确立研究对象，分析状态参量，列方程解方程。显然，研究问题的总思路是一致的，但具体操作又有不同。形成了方法的结构体系，就如同摆放有序的武器库，能随时针对不同的问题，灵活的提取不同的武器加以解决。
综合能力的考试，可以是在相结合的知识点上展开，也可以是在相结合的研究方法上展开。物理研究物质世界的基本结构和运动的最一般规律，因此，它有一些思想和方法也是最一般并且带有普遍意义的，不但适用于物理，而且适用于其它自然科学，如认识自然规律的普遍方法、实验的方法、建立理想化模型的方法等。有一些是物理学特殊的方法，如整体、隔离法，等效法，对称法，图象法，假设法，逆推法，极端法，近似法，微分法等。方法形成体系，将对形成综合能力起到事半功倍的作用。
第一节 力 学
一、知识结构
(一)质点的运动
1.深刻理解质点、位移、速度等基本概念；
2.认识参考系在描述物体运动时的重要作用，学会巧用相对速度；
3.对几种常见的质点运动规律，要掌握匀速直线运动，匀变速直线运动及曲线运动的特点及有关的公式。
(二)力和运动定律
1.理解重力、弹力、摩擦力及物体平衡，掌握物体受力分析的基本方法，会进行力的合成和分解。
2.理解物体平衡及力矩等概念，掌握共点力及固定转轴的物体的平衡条件。
3.掌握万有引力定律及其应用，理解第一、二、三宇宙速度及人造地球卫星的运行原理。
4.熟练掌握牛顿的三大定律及其应用，具体包括有：①理解惯性的概念，学会运用牛顿第一定律及惯性的概念解释有关物理现象。②掌握运用牛顿第二定律解题的基本方法。③理解作用力与反作用力的概念，注意区分其与平衡力的区别。④理解超重和失重现象，掌握解有关超重、失重问题的方法。⑤掌握物体受力与运动之间的关系，理解匀速圆周运动的特点及有关的概念，掌握向心力，向心加速度，线速度、角速度、周期之间的关系，了解离心现象及其应用。
(三)动量和机械能
1.正确理解动量和冲量的概念，知道他们的矢量性及单位。
2.理解动量定理，会用它分析有关的问题。
3.掌握动量守恒定律，会用动量守恒定律较为灵活地处理一维碰撞问题。
4.了解反冲运动及其应用。
5.理解功、功率、动能、重力势能，弹性势能的定义，掌握它们的计算公式；掌握动能定理，会运用动能定理解决力学问题；掌握重力做功与重力势能变化的关系。
6.理解功和能的关系，熟练掌握机械能守恒定律及其在解决力学问题中的灵活运用。
(四)机械振动和机械波
1.机械振动：①理解描述机械振动的物理量：位移、振幅、周期、频率等的意义；②明确简谐振动的特点；熟练掌握并灵活运用重要的简谐运动的模型——单摆的周期公式；③了解简谐运动图象的物理意义，学会“读、判、求、画”简谐运动的图象；④理解振动能量，自由振动和受迫振动的意义，知道共振产生的条件。
2.机械波：①掌握波长、波速、频率的概念及它们之间的关系；②理解波动图象的物理意义，掌握波动图象的“读、判、求、画”，注意波动图象和振动图象的区别；③了解波的迭加，掌握波的特有现象衍射，干涉产生的条件及《测定重力加速度》实验的原理、步骤和注意要点。
二、例题解析
例1 用长度为L的铁丝绕成一个高度为H的等螺距螺旋线圈。将它竖直地固定于水平桌面。穿在铁丝上的一珠子可沿此螺旋线无摩擦地下滑。这个小珠子从螺旋线圈最高点无初速滑到桌面经历的时间t= 。
【解析】测试学生利用常规物理知识(物体沿光滑斜面滑下)解决本题中的问题。考察学生等效思维能力和变通的能力。
将此螺旋线圈等效长为L，高为H的光滑斜面，倾角为θ。
t=
=
=
=
答案：L
例2 内燃打桩机锤头的质量m1=1800千克，钢筋混凝土桩的质量,m2=1600千克，锤头从距桩顶端上部1.5米的高度自由落下，打击三次后，桩刚好打入土层0.01米，求土层对桩的平均阻力。
【解析】此题可分为三个物理过程来分析，即锤自由下落过程，锤桩相碰过程，锤桩共同打入土层过程。
在第一过程中，是锤自由下落至刚接触桩的顶部，设h=1.5米，由自由落体末速度公式可求出锤刚接触桩顶时的速度v为：
v2=2gh，∴v=
在第二过程中，当锤和桩相碰时，可把锤和桩看成一个系统，并且相碰后一起向下运动，是完全非弹性碰撞，于是有：(1)锤桩相碰时的冲力属于内力，这个内力远大于它们的重力和土层对它们的阻力，所以，在这个过程中可认为系统不受外力。(2)由于相碰时间很短很短，虽然桩已得到速度v1，但还未向下运动，可认为桩还在原地。(3)碰撞时有能量损失(变为声能，内能等)，所以，动能不守恒。综上分析，可以得到系统的动量守恒，即：
(m1+m2)v1=m1v
第三过程中，锤、桩以速度v1共同向下运动打入土层静止，在这一过程中，由于桩受到土层的阻力，运动物体要克服阻力做功，所以，这一过程中动能和动量都不守恒。设三次打入土层的深度L=0.01米，则每次打入的深度为L/3米。设土层的平均阻力为f,根据动能定理得：-f
=
(m1+m2)v21
由上面三个过程得到的三个方程式可得
v1=
-f=
(m1+m2)()2·2gh
=
=
(牛)
≈牛
即f=-牛。负值表示土层的阻力方向和桩运动方向相反。
例3 如右图所示，质量为m的物体恰好能在倾角为α的斜面上匀速下滑，如在物体上施加一个力F使物体沿斜面匀速上滑，为了使得力F取最小值，这个力与斜面的倾斜角θ为多大?这个力的最小值是多少?如果要求力把物体从斜面的底端拉到最高点做功最少，求拉力的方向和所做的最小的功。(设斜面长l)
【解析】物体从斜面的上端恰好能匀速下滑，由平衡条件得
mg sin α＝μmg cos α
μ＝tg α
在F的作用下物体向斜面上运动的过程中，F的沿斜面分量及物体与斜面间的滑动摩擦力均与θ角的大小有关，在力F拉物体沿斜面匀速上升时，根据物体的平衡条件得(选沿斜面向上方向为x轴正方向，垂直于斜面向上为y轴正方向)：
F cosθ - mg sin α-f＝0 (1)
F sinθ + N – mg cos α＝0 (2)
其中N为斜面对物体的支持力，且f＝μN＝tgαN。由(1)、(2)两式可以解得
F＝
mg
上式中分子(sin α+μ cos α)mg是一个确定值，F的大小随分母变化。分母
cosθ+μsinθ＝
＝
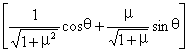
sin(φ＋θ)
当sin(φ＋θ)＝1，即φ＋θ＝90°时，分母最大F最小。
因为φ＝arctg
，所以θ＝90°-φ＝arctgμ时F取小值
mg。
物体从底到最高点力做功最少必须满足两个条件：其一是物体不受斜面的摩擦力，因为没有摩擦时物体在运动到最高点的过程中不需要克服摩擦力做功。其二是物体沿斜面的向上应该是匀速的，在匀速向上运动时，F所做的功不需要增加物体的动能，由以上两点可得
两式比，tgθ＝ctgα,θ＝
-α时F做功最少，根据F
sin θ＝mgcos α，
F＝
＝mg
Wmin＝F cos θl＝mgl sin α
小结：(1)本题第一部分求解必须知道被匀速拉上去是共点力作用下的平衡状态，满足平衡条件，然后用数学方法求得F的极小值。(2)第二问必须学会运用物理方法分析力在什么情况下做功最少。
例4 质量m=2kg的物体原来静止在粗糙水平地面上，现在第1、3、5、…奇数秒内给物体施加方向向北、大小为6N的水平推力，在第2、4、6、…偶数内，给物体施加方向仍向北，但大小等于2N的水平推力。已知物体与地面间的动摩擦因数为0.1，取g=10m/s2，求经过多长时间，物体位移的大小为40.25m。
【解析】该题是一道数理综合应用题。要正确顺利解答此题，既要有奇特巧妙的思路，又要做到数理知识的有机融合。
因为f=μmg=2N,所以，在奇数秒内F合=F-f=4N，物体做加速度为a=
2m/s2的匀加速运动；
在偶数秒内F合=F′-f=0，物体做匀速运动。显然，每一偶数秒内匀速运动的速度就是前一奇数秒内做匀加速运动的末速度，所以
第一个偶数秒内的速度v1=at；
第二个偶数秒内的速度v2=v1+at=2at；
第三个偶数秒内的速度v3=v2+at=3at;
……
第n个偶数秒内的速度vn=vn-1+at=nat。
又因为各奇数秒内物体运动的加速度相同，且后一奇数秒内的初速度正是前一奇数秒内的末速度，所以可以把各奇数秒内的匀加速运动连贯聚合起来看做一个完整的连续匀加速运动，则在n个奇数秒内物体通过的位移
∑S奇=a(nt)2=n2.(因a=2m/s2,t=1s) ①
而各偶数秒内的运动连贯聚合起来就是每个偶数秒速度不同的分段匀速直线运动，则在n个偶数秒内物体通过的位移
∑S偶=v1t+v2t+v3t…+vnt=(v1+v2+v3+…+vn)t
=(at+2at+3at+…+nat)t=(1+2+3+…+n)at2。
因为自然数数列之和sn=
,且a=2m/s,t=1s，所以
∑S偶=n(n+1) ②
从①式、②式可见，当n=4.5个奇数秒时，∑S奇=4.52m=20.25m；当n=4个偶数秒时，∑S偶 =4×(4+1)m=20m。即经过8.5s，物体位移的大小为40.25m。
例5 一个质点在平衡位置O点附近做简谐运动，若从O点开始计时，经过3s，质点第一次经过M点，如图所示；再继续运动，又经过2s，它第二次经过M点，则该质点第三次经过M点所需要的时间是（ ）
A.8s
B.4s
C.14s D.
s
【解析】设图中A、B两点为质点运动过程中的最大位移处，若开始计时刻质点从O点向右运动，O→M运动过程历时3s，M→B→M过程历时2s，显然
=4s，T=16s，质点第三次经过M点所需要的时间△t3=T-2=14s，故正确答案为C。
若开始计时时刻质点从O点向左运动，O→A→O→M运动过程中历时3s，M→B→M运动过程历时2s，显然
+ =4s，所以T=
s。因此质点第三次经过M点所需要的时间△t=T-2=-2=s,故正确答案为D。
综上分析，本题正确的答案为C、D。
例6 如右图所示，一个质量为M、各面均光滑的劈形物体，放在固定的斜面上，劈形
物体的上表面呈水平，其上放一质量为m的光滑小球，劈形物体从静止开始释放，不计空气阻力，小球在碰到斜面前的运动轨迹应是( )
A.平行于斜面向下的直线 B.竖直向下的直线
C.抛物线 D.无规则的曲线
【解析】假设小球在碰到斜面前的运动轨迹不是竖直向下的直线，而是平行于斜面向下的直线，或是抛物线，或是无规则的曲线，那幺小球除刚开始速度为零外，在运动过程中不但在竖直方向速度有变化，而且在水平方向速度有变化。若小球在水平方向速度有变化，则小球在水平方向必受外力作用。因为该球是光滑球，劈形物体的上表面也是有的，劈形物体的上表面对球无水平方向的摩擦力，所以小球在水平方向无外力作用(找不到对小球施水平力的物体!)原来的假设是不成立的，本题的正确选项是B。
例7 如图所示，由于机器带动竖直轴转动，使长为l的轻绳拴着质量为m的小球在水平面做匀速圆周运动，轻绳的运动轨迹为圆锥曲面。开始绳与竖直方向的夹角为30°，后来机器转动速度加大，使绳与竖直方向的夹角变为60°。在此过程中，机器对小球做的功为多大?
【解析】本题是动能定理与匀速圆周运动的综合题，当小球在水平面内做圆锥摆运动时，轻绳的拉力与重力的合力提供向心力，一定沿半径指向圆心，轻绳与竖直方向夹角增大时，所受向心力增加，小球线速度增大，动能增大，同时小球的位置升高，重力势能增大，重力做负功，根据动能定理可求出机器对小球做的功。
设轻绳与竖直杆夹角为θ，对小球受力分析如图，小球所受合力F=mgtgθ，小球运动半径r=lsinθ，由牛顿第二定律
mgtgθ=m
mv2=mgltgθsin
当θ=30°时 mv21=mgltg30°sin30°
当θ=60°时 mv22=mgltg60°sin60°
小球上升的高度h=l(cos30°-cos60°)
设机器做功W，由动能定理
W-mgh=△EK=mv22-mv21
W=mgl(tg60°sin60°-tg30°sin30°)+mgl(cos30°-cos60°)
=0.97mgl
例8 在光滑水平地面上放有一质量为M带光滑弧形槽的小车，一个质量为m的小铁块以速度v沿水平槽口滑去，如右图所示，求：
(1)铁块能滑至弧形槽内的最大高度H；(设m不会从左端滑离M)
(2)小车的最大速度；
(3)若M=m，则铁块从右端脱离小车后将作什么运动?
【解析】(1)当铁块滑至弧形槽中的最高处时，m与M有共同的水平速度，等效于完全非弹性碰撞，由于无摩擦力做功，做系统减小的动能转化为m的势能。
根据系统水平动量守恒：mv=(M+m)v′，
而 mgH=mv2- (m+M)v′2，
可解得 Hm=Mv2/［2g(M+m)］
(2)当铁块滑至最大高度后返回时，M仍在作加速运动，其最大速度是在铁块从右端脱离小车时，而铁和小车间挤压、分离过程，属于弹性碰撞模型，有：
mv=mvm+MVM (1)
mv2=mv2m+Mv2M
(2)
由(1)、(2)式得vm=
v,vM=
v
所以，小车的最大速度为2mv/(M+m)
(3)当M=m时，v′m=0,vM=v，铁块将作自由落体运动。