高三物理巧用极限法分析临界问题
临界问题的分析是中学物理中较为常见，也是很多同学感到困难的问题之一，这就要求我们在教学中能不断探索这类问题的分析方法。
极限法分析临界问题，是通过分析把关键物理量同时推向极大和极小时的物理现象，从而找出解决问题的突破口的一种方法。下面通过几种情况的分析来体会：
一、关键物理量“力F”
【例1】如图1所示，物体A的质量为2kg，两轻绳AB和AC(LAB=2LAC)的一端连接在竖直墙上，另一端系在物体A上，今在物体A上另施加一个与水平方向成α=600角的拉力F。要使两绳都能伸直，试求拉力F的大小范围。(g=10m/s2)
分析与解 如果F很小，由竖直方向平衡知轻绳AB
中必有张力，当AC中张力恰为零时，F最小；如果F很
大，由竖直方向平衡知轻绳AC中必有张力，当AB中张
力恰好为零时，F最大。
设物体的质量为m，轻绳AB中的张力为TAB，AC
中的张力为TAC，F的最小值为F1，最大值为F2
LAB=2LAC，有∠CAB=600
由平衡条件有：
F1sin600+TABsin600=mg , F1cos600=TABcos600
F2sin600=mg
以上各式代入数据得：F1=20√3/3N，F2=40√3/3N
因此，拉力F的大小范围：20√3/3N ＜F＜40√3/3N
此题也可由平衡条件直接列方程，结合不等式关系TAB＞0，TAC＞0求解。
二、关键物理量“加速度a”
【例2】质量为0.2kg的小球用细绳吊在倾角θ=600的斜面体的顶端，斜面体静止时，小球紧靠在斜面上，线与斜面平行，如图2所示，不计摩擦，求当斜面体分别以（1）2√3m/s2，（2）4√3m/s2的加速度向右加速时，线对小球的拉力。
分析与解 很多同学看到题目就会不加分析的列方程
求解，从而出现解出的结果不符合实际。其实，如果我们
仔细审题就会发现题目设问的着眼点是加速度。当小球向
右加速运动时，如果加速度a很小，小球压紧斜面，受力
分析如图2—1；如果加速度a很大，小球将离开斜面，受
力分析如图2—2。
设小球对斜面的压力为零时，斜面体的加速度为a0
（即临界加速度），受力分析得：a0=gcotθ=10√3/3（m/s2）
（1）因为a=2√3（m/s2）＜a0，因此小球仍压紧斜面，
由牛顿第二定律和平衡条件列方程有：
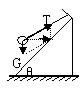Tcosθ-Nsinθ=ma , Tsinθ+Ncosθ=mg
代入数据解得：T=m（gsinθ+acosθ）=1.2√3 N
（2）因为a=4√3 m/s2＞a0，因此小球已飘离斜面，
|
T=m√g2+a2=0.4√37 N （此处也可按（1）的列式
方法求解）。
三、关键物理量“速度v /ω”
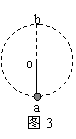【例3】如图3所示，细杆的一端与一小球相连，可绕过O点的水平轴自由转动。现给小球一初速度，使它做圆周运动，图中a、b分别表示小球轨道的最低点和最高点，则杆对球的作用力可能是（ ）
A、a处为拉力，b处为拉力 B、a处为拉力，b处为推力
C、a处为推力，b处为拉力 D、a处为推力，b处为推力
分析与解 a处的分析很容易，只能为拉力；而b处则有两种
可能。当v或ω很小时，小球的重力大于所需的向心力，杆对球
的作用力为推力；v或ω很大时，小球的重力不足以提供小球所需
的向心力，杆对小球的作用力为拉力。故正确答案为AB
【例4】如图4—1所示，在互相垂直的匀强电场和匀强磁场中，一个质量为m、带电量为+q的有孔小球沿着穿过它的竖直长杆下滑，小球与杆之间的滑动摩擦系数为μ，设电场场强为E，磁感应强度为B，电场、磁场范围足够大，求：（1）当小球有最大加速度时的速度为多大？（2）当小球有最小加速度时的速度为多大？
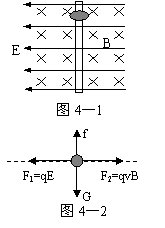分析与解 对小球受力分析，如图4—2，开始
速度很小，所受的杆的弹力向右，大小N=qE-qvB，
随着速度的增大，N减小，f=μN减小，加速度
a=（G-f）/m增大；小球速度很大时，所受弹力向左，
大小为N= qvB –qE，随着速度的增大，N增大，
f=μN增大，加速度a=（G-f）/m减小，直至为零。
（1）当N= qvB –qE =0时，小球有最大加速度
v=E/B。
（2）小球的最小加速度为a=0，则有
mg=f ，f=μN ，N= qvB –qE
由以上各式解得：v=mg/μqB+E/B
四、关键物理量“动量 / 冲量”
【例5】宇航员在某一星球上以速度v0竖直向上抛出一个小球，经过时间t，小球又落回到原抛出点。然后他用一根长为l的细绳把一个质量为m的小球悬挂在O点，使小球处于静止状态，如图5所示，现在最低点给小球一个水平向右的冲量I，使小球能在竖直平面内运动，若小球在运动的过程中始终对
细绳有力的作用，则冲量I应满足什么条件？
分析与解 如果给小球的冲量I很小，小球在竖直平面
内摆动，细绳中必有张力；如果给小球的冲量I很大，小球
在竖直平面内做圆周运动，只要过最高点时的速度大于临界
速度，细绳中也有张力。
宇航员所在星球的重力加速度：g=2v0/t
设使小球在竖直平面内摆动的最大冲量为I1，小球获得
的初速度的最大值为v1，由机械能守恒定律：
（1/2）mv12=mgl
解得I1=m v1=2m√v0l/t
设使小球在竖直平面内做圆周运动的最小冲量为I2，小球获得的初速度的最小值为v2，小球过最高点的临界速度为v临
由机械能守恒定律：（1/2）mv临 -（1/2）mv22= - mg2l
由牛顿第二定律与向心力公式：mg=mv临2/l
解得I2=m v2=m√10v0l/t
所以，要使小球在运动过程中始终对细绳有力的作用，给小球的冲量：
I＜2m√v0l/t或I＞m√10v0l/t
五、关键物理量“磁感强度B”
【例6】M、N两板间相距为d，板长均为5d，两板未带电，板间有垂直纸面的匀强磁场，如图6—1所示，一大群电子沿平行于板的方向从各处位置以速度v射入板间，为了使电子都不从板间穿出，磁感强度B的范围应为多少？
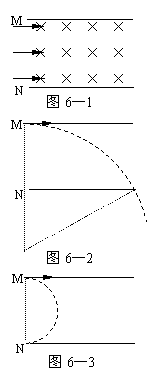分析与解 根据左手定则，电子受洛仑兹力向下，
只要从板的最上端进入的电子不从板间穿出，则所有
电子都不会从板间穿出。如果B很小，电子运动的轨
道半径很大，将会从板的右端穿出，当电子恰好从N
板的右边缘穿出时，B最小（如图6—2）；如果B很
大，电子运动的轨道半径很小，将会从板的左端穿出，
当电子恰好从N板的左边缘穿出时，B最大。（如图
6—3）
设电子不从板间穿出，磁感应强度最小值为B1，
轨道半径为R1，电子的质量为m，带电量为e，则有：
mv2/R1=evB1， R12=（5d）2 +（R1-d）2
解得B1=mv/13de
设电子不从板间穿出，磁感应强度最大值为B2，
轨道半径为R2，电子的质量为m，带电量为e，则有：
m v2/R2=evB2 ， 2R2=d
解得B2=2mv/de
因此，电子不从板间穿出，磁感强度B的范围是
mv/13de＜B＜2mv/de
六、关键物理量“厚度d”
|
（1）求每种波长的光入射玻璃板上表面后的折射角；
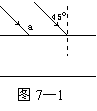（2）为了使光束从玻璃板下表面出射时能分成不交叠的两束，玻璃板的厚度d至少为多少？
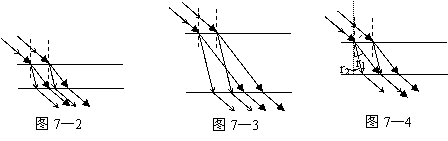
分析与解 两种波长的光射到玻璃板表面后，
如果玻璃板的厚度d较小，光束从下表面出射时，
仍相互交叠，如图7—2；如果玻璃板的厚度d较
大，光束从下表面出射时，将分成不交叠的两束，
如图7—3，临界厚度如图7—4。
 |
（1）设入射角为i，经玻璃板折射后，折射率为n1的光的折射角为r1，折射率为n2的光的折射角为r2，根据折射定律：n1=sini/sinr1 ，n2=sini/sinr2
代入数据解得：r1=arcsin√2/3 ，r2=arcsin√6/6
（2）如图9—3，由几何关系有：dtanr1 – dtanr2
= √2 a
又tanr1=√14/7 ，tanr2 =√5/5
代入数据解得：d= 70a/（10√7 – 7√10）
极限法分析临界问题在解题中的应用远不止这些，只要我们用心体会，定会收益匪浅，深感其妙。