高三物理热 学
(时间: 60分钟, 满分:100分)
一、选择题(每题5分)
1.布朗运动的发现,在物理学上的主要贡献是 [ ]
A.说明了悬浮微粒时刻做无规则运动
B.说明了液体分子做无规则运动
C.说明悬浮微粒无规则运动的激烈程度与温度有关
D.说明液体分子与悬浮微粒间有相互作用力
2.两个分子甲和乙相距较远(此时它们之间的分子力可忽略),设甲固定不动,乙逐渐靠近甲直到不能再靠近的整个过程中
[ ]
A.分子力总是对乙做正功
B.乙总是克服分子力做正功
C.先是乙克服分子力做功,然后分子力对乙做正功
D.先是分子力对乙做正功,然后乙克服分子力做功
3.一定质量的0℃的水,变成0℃的冰时,体积膨胀则
[ ]
A.分子平均动能减少,分子势能增加
B.分子平均动能增大,分子势能减少
C.分子平均动能不变,分子势能减少
D.分子平均动能不变,分子势能增大
4.一定质量的气体,可经不同的过程从状态1(P1V1T1)变到状态2(P2V2T2),已知T2〉T1,则在这过程中
[ ]
A.气体一定从外界吸收热量
B.气体和外界交换的热量都是相等的
C.外界对气体做的功都是相等的
D.气体内能的变化量都是相等的
5.在一个上下水温均匀,并保持恒温的水池中,有一个小气泡缓慢上升,则上升过程中正确的说法是(设泡内为理想气体) [ ]
A.气泡内能减少,放出热量
B.气泡内能不变,对外做功,吸收热量
C.气泡内能不变,不放热也不吸热
D.气泡内能增加,吸收热量
6.如图所示,a和b为一定质量的某种理想气体的两条等容图线,如果气体由状态A变到状态B,则此过程中关于气体的正确说法是 [ ]
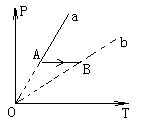
A.外界不做功,吸热,内能增加
B.外界做功,放热,内能减少
C.不对外界做功,放热,内能减少
D.对外界做功,吸热,内能增加
7.一端封闭粗细均匀的玻璃管内,用一段水银柱封闭了一部分气体,当玻璃管开口向上竖直放置时,管内空气柱长度为L,如图所示,当玻璃管自由下落时,空气柱的长度将 [ ]
![]()
A.增长 B.减小 C.不变 D.不能确定
8.如图所示,U形管两臂竖直固定,一小段水银柱A与管底部水银间有一段空气柱B被封于右臂管子的中部,设U形管内粗细均匀,两端均开口与大气相通,现再向左管注入一些水银,等平衡后可知 [ ]
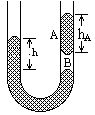
A.空气柱B的压强增大
B.空气柱B的长度变小
C.图中h与hA长度相等
D.图中h比原来增大
9.如图所示,一个绝热活塞P把容器分隔成A、B两部分,它们的容积之比是1∶3,A、B内装有同种气体,温度均为t1=0℃,此时活塞处于平衡状态,现将两部分气体温度都升高到t2=273℃,则活塞将 [ ]
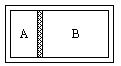
A.仍保持平衡状态 B.向右移动
C.向左移动 D.左右运动
10.如图所示,是一定质量气体的P-V图线,在这些图线中,能反映出气体在状态A时内能大于状态B的是 [ ]
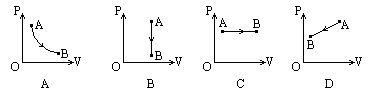
二、填空题(每题5分)
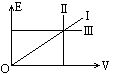
11.如图所示,表示一定质量理想气体,在等压、等温、等容变化过程中内能E和体积V的关系图线,则E-V图中反映等温变化过程的图线是 ,反映等压变化过程的图线是 ,反映等容变化过程的图线是 .
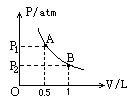
12.如图所示,为0.05mol理想气体的等温图线,A、B是变化过程中的两个状态,则状态B的压强P2= ,这条等温线,表示它的温度是 ℃.
13.如果大气压为P,已知水下某一深度为h处,有一个气泡,该气泡的半径为在水面时半径的1/2,可知该气泡距水面的深度h= .
14.空气在标准状态下的密度是1.12×10-3kg/L,当温度升高到83℃,压强增大到2atm时,空气的密度是 kg/L.
三、计算题(每题10分)
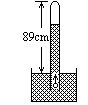
15.如图为托里拆利实验装置,管内横截面积为1cm2,此时,大气压强为75cm水银柱高,若实验中不慎有一个体积为0.2cm3的气泡从管口进入管内,并上升至管顶部,求管内水银面的高度差.
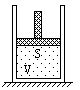
16.一圆筒形气缸静置于地面上,如图所示,气缸筒的质量为M,活塞(连同手柄)的质量为m,气缸内部的横截面积为S,大气压强为P0,平衡时气缸内的容积为V,现用手握住活塞柄缓慢向上提,设气缸足够长,在整个上提过程中,气体温度保持不变,并不计气缸内气体的重力及活塞与气缸壁的摩擦,求将气缸刚提离地面时,活塞上升的高度.
17.如图所示,气缸A和B,分别置于水平台上,它们的横截面积之比为1∶2,分别用活塞封住一部分气体,两活塞间用一连杆连接在一起,在气缸内可无摩擦滑动.在温度为27℃,大气压强为1.0×105Pa时,A气缸内气体的压强为2×105Pa,活塞均处于平衡状态,求:(1)此时B气缸内气体的压强;(2)当两气缸内气体的温度都变化相同的△t时,活塞运动状态将如何变化?
参考答案
一、选择题
1.B 2.D 3.C 4.D 5.B
6.D 7.A 8.C 9.A 10.BD
二、填空题
11. Ⅲ,Ⅰ,Ⅱ
12. 1atm,-29
![]()
14. 1.72×10-3
三、计算题
15.解:以气泡为研究对象
初态:P1=75cmHg, V1=0.2cm3
末态:P2=(75-h)cmHg, V2=(89-h)Scm3
根据玻意耳定律P1V1=P2V2
75×0.2=(75-h)(89-h)×1
解得:h=74cm(舍去不合理的答案)
16.解:以气缸内的气体为研究对象,设活塞上升距离为x,
![]()
末态:以气缸为研究对象,对它进行受力分析,如图所示,
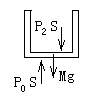
根据平衡条件:
有Mg+P2S-P0S=0, 得P2=P0-Mg/s, V2=V+xS
根据玻意耳定律P1V1=P2V2
![]()
![]()
17.解:
(1)两活塞均处平衡状态,根据平衡条件,
(PA-P0)SA=F1......(1)
(PB-P0)SB=F2......(2)
F1=F2......(3)
由(1)(2)(3)解得,PB=1.5×105Pa
(2)设活塞不移动,则缸内气体体积不变,根据查理定律,
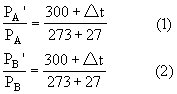
![]()
若Δt为正值,则温度升高,压强应增大,
设PA′ 为2.4×105Pa
![]()
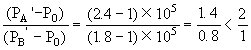
![]()
若Δt为负值,则温度降低,压强减小,
![]()
![]()
![]()
两气缸内气体温度发生变化时,活塞不能处于平衡状态,
当温度升高时,活塞将从B向A移动,当温度降低时,
活塞将从A向B移动.