磁场必做题
A1、(94全国)质子和α粒子在同一匀强磁场中作半径相同的圆周运动.由此可知质子的动能E1和α粒子的动能E2之比E1:E2等于多大？
A2、（93全国）如图19-19所示,一带电质点,质量为m,电量为q,以平行于Ox轴的速度v从y轴上的a点射入图中第一象限所示的区域.为了使该质点能从x轴上的b点以垂直于Ox轴的速度v射出,可在适当的地方加一个垂直于xy平面、磁感应强度为B的匀强磁场.若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径.重力忽略不计.
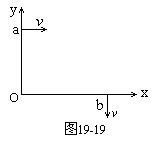
B1、（96全国）设在地面上方的真空室内存在匀强电场和匀强磁场.已知电场强度和磁感应强度的方向是相同的,电场强度的大小E=4.0伏/米,磁感应强度的大小B=0.15特.今有一个带负电的质点以v=20米/秒的速度在此区域内沿垂直场强方向做匀速直线运动,求此带电质点的电量与质量之比q/m以及磁场的所有可能方向(角度可用反三角函数表示).
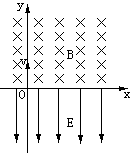
B2、（98全国）如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E。一质量为m，电量为-q的粒子从坐标原点O沿着y轴正方向射出。射出之后，第三次到达x轴时，它与点O的距离为L。求此粒子射出时的速度v和运动的总路程s（重力不计）。
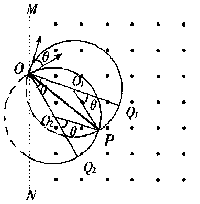
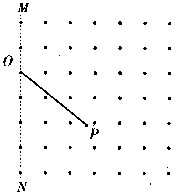C1、（99全国）图中虚线MN是一垂直纸面的平面与纸面的交线，在平面右侧的半空间存在一磁感强度为B的匀强磁场，方向垂直纸面向外是MN上的一点，从O点可以向磁场区域发射电量为＋q、质量为m 、速率为的粒于，粒于射入磁场时的速度可在纸面内各个方向已知先后射人的两个粒子恰好在磁场中给定的P点相遇，P到0的距离为L不计重力及粒子间的相互作用
(1)求所考察的粒子在磁场中的轨道径
(2)求这两个粒子从O点射人磁场的时间间隔
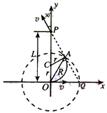
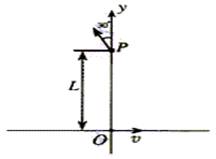C2、（04全国4）一匀磁场，磁场方向垂直于xy平面，在xy平面上，磁场分布在以O为中心的一个圆形区域内。一个质量为m、电荷量为q的带电粒子，由原点O开始运动，初速为v，方向沿x正方向。后来，粒子经过y轴上的P点，此时速度方向与y轴的夹角为30°，P到O的距离为L，如图所示。不计重力的影响。求磁场的磁感强度B的大小和xy平面上磁场区域的半径R。
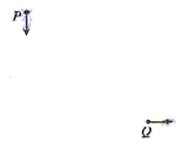
D2、（04全国老课程）空间中存在方向垂直于纸面向里的匀强磁场，磁感应强度为B，一带电量为+q、质量为m的粒子，在p点以某一初速开始运动，初速方向在图中纸面内如图中P点箭头所示。该粒子运动到图中Q点时速度方向与P点时速度方向垂直，如图中Q点箭头所示。已知P、Q间的距离为l。若保持粒子在P点时的速度不变，而将匀强磁场换成匀强电场，电场方向与纸面平行且与粒子在P点时速度方向垂直，在此电场作用下粒子也由P点运动到Q点。不计重力。求：
|
（2）两种情况中粒子由P
运动到Q点所经历的时间之差。
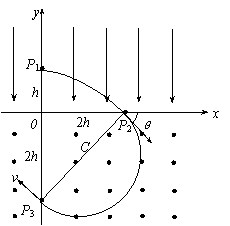
D1、（04全国1）如图所示，在y＞0的空间中存在匀强电场，场强沿y轴负方向；在y＜0的空间中，存在匀强磁场，磁场方向垂直xy平面（纸面）向外。一电量为q、质量为m的带正电的运动粒子，经过y轴上y＝h处的点P1时速率为v0，方向沿x轴正方向；然后，经过x轴上x＝2h处的 P2点进入磁场，并经过y轴上y＝
处的P3点。不计重力。求
（l）电场强度的大小。
（2）粒子到达P2时速度的大小和方向。
（3）磁感应强度的大小。
|
答案
A1、（略）
A2、质点在磁场中作半径为R的圆周运动,
根据题意,质点在磁场区域中的轨道是半径等于R的圆上的1/4圆周,这段圆弧应与入射方向的速度、出射方向的速度相切.过a点作平行于x轴的直线,过b点作平行于y轴的直线,则与这两直线均相距R的O′点就是圆周的圆心.质点在磁场区域中的轨道就是以O′为圆心、R为半径的圆(图中虚线圆)上的圆弧MN,M点和N点应在所求圆形磁场区域的边界上.
在通过M、N两点的不同的圆周中,最小的一个是以MN连线为直径的圆周.所以本题所求的圆形磁场区域的最小半径为
所求磁场区域如图中实线圆所示.
B1、根据带电质点做匀速直线运动的条件,得知此带电质点所受的重力、电场力和洛仑兹力的合力必定为零.由此推知此三个力在同一竖直平面内,如右图所示,质点的速度垂直纸面向外.
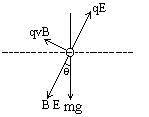
解法一:由合力为零的条件,可得
求得带电质点的电量与质量之比
因质点带负电,电场方向与电场力方向相反,因而磁场方向也与电场力方向相反.设磁场方向与重力方向之间夹角为θ,则有
qEsinθ=qvBcosθ,
即磁场是沿着与重力方向夹角θ=arctg0.75,且斜向下方的一切方向.
解法二:因质点带负电,电场方向与电场力方向相反,因而磁砀方向也与电场力方向相反.设磁场方向与重力方向间夹角为θ,由合力为零的条件,可得
qEsinθ=qvBcosθ, ①
qEcosθ+qvBsinθ=mg, ②
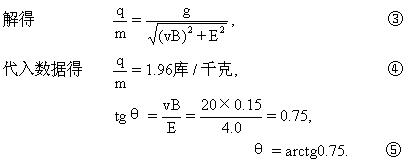
即磁场是沿着与重力方向成夹角θ=arctg0.75,且斜向下方的一切方向
B2、粒子运动路线如图示有
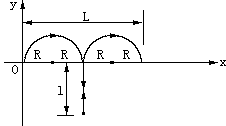
L＝4R ①
粒子初速度为v，则有
qvB=mv2/R ②
由①、②式可算得
v=qBL/4m ③
设粒子进入电场作减速运动的最大路程为l，加速度为
a，v2=2al ④
qE=ma ⑤
粒子运动的总路程 s=2πR+2l ⑥
由①、②、④、⑤、⑥式，得s=πL/2+qB2L2/(16mE) ⑦
C1、（1）设粒子在磁场中作圆周运动的轨道半径为R，由牛顿第二定律，有
qvB=mv2/R 得R=mv/qB ①
（2）如图所示，以OP为弦可画两个半径相同的圆，分别表示在P点相遇的两个粒子的轨道。圆心和直径分别为 O1、O2和OO1Q1,OO2Q2,在0处两个圆的切线分别表示两个粒子的射入方向，用θ表示它们之间的夹角。由几何关系可知
| ∠PO1Q1=∠PO2Q2θ ② 从0点射入到相遇，粒子1的路程为半个圆周加弧长Q1P Q1P＝Pθ ③ 粒子2的路程为半个圆周减弧长PQ2=2 PQ2=Rθ ④ 粒子1运动的时间 t1=(1/2T)+(Rθ/v) ⑤ 其中T为圆周运动的周期。粒子2运动的时间为 t2=(1/2T)-(Rθ/v) ⑥ 两粒子射入的时间间隔 △t=t1-t2=2Rθ/V ① 因 Rcos(θ/2) =1/2L 得 θ =2arccos (L/2R) ③ 由①、①、③三式得 △t=4marccos(lqB/2mv)/qB |
|
C2、粒子在磁场中受各仑兹力作用，作匀速圆周运动，设其半径为r，
|
①
据此并由题意知，粒子在磁场中的轨迹的圆心C必在y轴上，
且P点在磁场区之外。过P沿速度方向作延长线，它与x轴相交
于Q点。作圆弧过O点与x轴相切，并且与PQ相切，切点A即
粒子离开磁场区的地点。这样也求得圆弧轨迹的圆心C，如图所示。
由图中几何关系得
L=3r ②
由①、②求得
③
图中OA的长度即圆形磁场区的半径R，由图中几何关系可得
（1）粒子在磁场中做匀速圆周运动，以v0表示粒子在P点的初速度，R表示圆周的半径，则有 qv0B=m
①
由于粒子在Q点的速度垂直它在p点时的速度，可知粒子由P点到Q点的轨迹为
圆周，故有 
②
以E表示电场强度的大小，a表示粒子在电场中加速度的大小，tE表示粒子在电场中由p点运动到Q点经过的时间，则有
qE=ma ③
④
R=v0tE ⑤
由以上各式，得 
⑥
（2）因粒子在磁场中由P点运动到Q点的轨迹为圆周，故运动经历的时间tE为圆周运动周期T的，即有 tE=T ⑦
而 
⑧
由⑦⑧和①式得
⑨
由①⑤ 两式得 
⑩
11
④
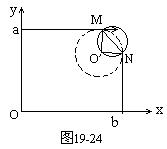
D2、（1）粒子在电场、磁场中运动的轨迹如图所示。设粒子从P1到P2的时间为t，电场强度的大小为E，粒子在电场中的加速度为a，由牛顿第二定律及运动学公式有
qE ＝ ma ①
v0t ＝ 2h ②
③
由①、②、③式解得
④
（2）粒子到达P2时速度沿x方向的分量仍为v0，以v1表示速度沿y方向分量的大小，v表示速度的大小，θ表示速度和x轴的夹角，则有
⑤
⑥
⑦
由②、③、⑤式得
v1＝v0 ⑧
由⑥、⑦、⑧式得
⑨
⑩
（3）设磁场的磁感应强度为B，在洛仑兹力作用下粒子做匀速圆周运动，由牛顿第二定律
⑾
r是圆周的半径。此圆周与x轴和y轴的交点分别为P2、P3。因为OP2＝OP3，
θ＝45°，由几何关系可知，连线P2P3为圆轨道的直径，由此可求得
r＝
⑿
由⑨、⑾、⑿可得
⒀