高中物理专题一：常见的物理解题方法
专题新平台
本专题将介绍物理解题中几种常用的方法
一、分解的方法
分解是人类了解复杂事物、解决复杂问题时最常用的方法之一。医院里分内、外科等，是将复杂的人体分解，以便把握各类疾病的规律；要想了解小闹钟的构造特征，最直接的方法是将其分解―――拆开看看；甚至连吃西瓜时先将西瓜切成几片，也可以说是借助于分解的手段（切开）解决了整个西瓜无法囫囵吞下的“难题”。物理解题也是这样，对物理问题中所给出的复杂运动、复杂过程，对物理问题中所涉及的复杂事物、复杂模型等，均可以借助于分解的手段予以简化。
二、几何的方法
物理学涉及到的物理量中，相当一部分是既有大小又有方向的矢量，而反映物理量间关系的物理规律中，也有相当多的一部分是反映矢量间的关系，这些矢量间的关系除了反映各物理量的物理意义间的本质联系外，其数学表现形式实际上给出的是某种几何关系。因此，运动几何的方法来处理矢量间的几何关系就成了物理解题中的常用方法。从思维科学的角度来看，几何的方法的本质在于思维方式的转换―――化抽象思维为形象思维。
三、图象的方法
解决物理问题的依据主要是相应的物理规律，定量给出的物理规律实际上就是物理量间的函数关系式，而采用数、形转换这一解析几何的手段将给出的函数关系式以图象的形式表现出来就称为函数的图象，它和用公式的形式给出的物理规律相比，除了表现的形式不同外，其物理本质应该是一致的。因此，在应用物理规律解决物理问题时，既可以用公式的表达形式，也可以用图象的表达形式。和几何的方法一样，图象的方法也是一种化抽象为形象的方法，但应该注意，与几何的方法关注着矢量间方位的几何关系不同的是，图象的方法关注的是由函数图象的形式给出的物理量间的数量关系。
四、等效的方法
等效代换作为物理解题中的常用方法之一，通常有“过程等效代换”和“模型等效代换”两大类，也就是说，通过等效的方法，我们或者可以将较为复杂的物理过程转换为较为简单的物理过程；或者可以把较为复杂的事件转换为相对简单的物理模型。和几何方法及图象方法相比，其相同之处是等效的方法的基本思想也是所谓的“转换思想”；其不同之处则是，等效的方法是通过转换思维活动的作用对象（物理过程和物理模型）以降低思维活动的难度，而几何的方法及图象的方法则是通过转换思维活动自身的形式（把抽象思维转换为形象思维）来降低思维活动的难度的。
必须强调的是：等效的方法的应用，应该受到“效果相同”的基本原则的制约，而对所谓的“效果相同”的理解，则应关注到“效果”这一概念的“多侧面”的特性。具体地讲，在如图所示的物块上的a、b两点分别作用大小与方向均相同的水平推力和水平拉力，就改变物块的转动状态而言，这两个力就不等效了。
五、模型的方法
任何物理过程都是由具体的物理模型所参与的，如果参与物理过程的物理模型具有鲜明的特征，则往往会将这鲜明的特征带入它所参与的物理过程之中，这就给我们一种“借助于了解参与物理过程的物理模型的特征去把握物理过程的特征”的方法，即所谓的“模型的方法”。
一般来说，特征鲜明的物理模型往往是以参与物理过程的实际装置为背景，将其次要因素忽略而使其主要因素明显地凸现出来而构建起来的。在一些从生产、生活实践中出发的物理问题中，参与物理过程的物理模型的抽象程度一般较低，这就要求以模型的方法求解这类问题，首先要把握物理模型的关键性因素构建起抽象程度高、特征表现明显的物理模型，而这种模型的构建过程，其实质就是借助于某种特定的思维活动方式，去把握物理模型的本质特征，进而把握物理模型所参与物理过程的本质特征。
六、平均的方法
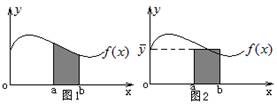“平均”概念的本意，通常应作如下理解：若物理量y随另一物理量x变化关系为：
；在xoy平面内上述函数关系所对应的函数图象如图1所示，若取某一给定的区间：
；在这区间内函数图象下的“面积”为S（图2中阴影部分），并令S＝（b-a）
，其中的几何意义相当于图中“面积”也为S的阴影矩形的高，则把称为：物理量y在区间上对物理量x的平均值。由此可见：“平均”概念存在着如下两个重要的前提。
（1）首先必须指明所提出的“平均”概念是对什么物理量的平均；（2）其次还必须明确所提出的“平均”概念是在什么区域内求得平均。
平均的方法，从思维的角度看，实质上是建立在转化的思想基础上的一种特殊的思维方式，通过取平均值的操作，用相对稳定的平均值取代不断变化的物理量。特别应该指出的是：对于某种随x均匀变化的物理量y来说，物理问题的分析中经常采用“平均的方法”，因为此时的平均值往往等于y在均匀变化的区间内始、末值的和的一半，即：
七、假设的方法
在一些物理问题中，所涉及到的物理过程的发生、发展以及变化的方向存在着多种可能性，而在对这些过程作出定量分析之前，往往很难对各种可能性作出正确的取舍，于是，这就需要运用所谓的“假设法”，该方法的一般操作程序如下：
（1）对物理过程作出粗略的定性或半定量分析，明确过程的发展、变化所存在的各种可能性Ai（i=1,2,┉k,┉,n）；
（2）在过程发展、变化所存在的各种可能性中不失一般性地作出假设：Ai为真；
（3）在“Ai为真”这一假设的基础上运用相应的物理规律对物理过程进一步作出精确的定量分析，求得相应的结论Bi；
（4）以相应的后继检验手段Ck进行验证，以确定Ak 的真伪，进而确定相应的结论Bk的真伪；
应当注意的是：在物理发展、变化的众多可能性中选择一种并假设其为真时，第一应该做到的是“不失一般性”；第二则应同时考虑到与该假设相关的后继检验手段的确定。因为从思维规律上讲，建立在未经过检验的假设基础上的任何结论都是不可靠的。
八、微元的方法
作为一种特殊的思维方法“微元法”在被应用于物理解题时，常能将题中给出的变化的事物和题中所涉及到的变化过程转化为简单的不变的事物和不变的过程来处理。之所以能做到这一点，是因为“微元法”抓住了“任何变化都必须在一定的时、空范围内才得以实现”这一本质特征。借助于选取“微元”这一手段来限制变化赖以实现的时、空，从而使变化的事物与过程在极短的时间和极小的空间内，均可视为不变的事物与不变的过程。
1、“微元法”的操作程序是：
（1）适当地读取微元Δx，用以量化题中给出的事物的“元事物”或是题中反映过程的“元过程”；
（2）视所取的微元对应的“元事物”或“元过程”为恒定，根据相应的物理规律给出待求量y 的微元Δy=f(x)Δx；
（3）在上式的定义域S：内施以叠加演算，进而求得题中所给完整事物或题中反映的完整过程的解：
2、“微元法”在选取微元时，应遵循如下几个基本原则：
（1）可加性原则：由于所选取的微元Δx最终必须参与叠加演算，因此对微元Δx所对应的量x提出了一个最基本的要求：必须是一个具有“可加性”特征的物理量。
（2）有序性原则：为了保证所选取的微元Δx所对应的Δy能够在所给出的定义域内较为方便地获得不遗漏、不重复的完整的叠加，因此在选取微元Δx时还应注意到必须按照某种特定的顺序来进行。
（3）平权性原则：对于所选取的微元Δx对应的Δy，在相应的定义域内叠加演算实际上是以
为权函数的加权叠加，而这种加权叠加在最为一般的意义上，实质上就是求定积分，
若当权函数具备形如＝k（常量）的所谓的“平权”的特征，即权函数在叠加的区域内处处相等，那么，叠加演算中复杂的定积分将转化为简单的数学操作
，因此，为使“微元法”中复杂的叠加演算转化为上述所示的简单形式，选取微元Δx时还应遵守所谓的“平权性原则”，即使权函数在定义域内处处相等（平权）
高考专题新例析
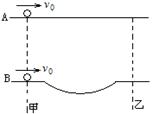例题1，如图所示，A、B两小球同时从甲点出发以相同的初速度v0向乙点运动，A球沿水平路面一直运动到乙点，B球在运动途中经过一段凹形路面，若B球始终不离开路面，且两球均不受摩擦的作用，则：
A、两球同时到达乙点； B、A球先到达乙点；
C、B球先到达乙点； D、条件不足，无法确定；
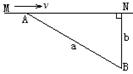例题2、如图所示，质点A沿直线MN以速度v做匀速运动，开始时质点B与A相距为a，与MN间的垂直距离为b，则质点B沿什么方向做匀速直线运动能以最小的速度与质点A相遇？这最小速度为多大？
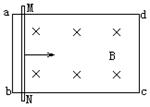例题3、如图所示，硬质粿导线做成的闭合矩形线框abcd固定在匀强磁场中，ab＜bc，磁场方向与线框平面垂直。另一段同种规格的导线MN与导线框保持良好的接触，在外力作用下从导线框的左端匀速滑至右端，在这一过程中，导线框中消耗的电功率的变化情况是：（ ）
A、保持恒定； B、先变大后变小；
C、先变小后变大； D、以上结论都不对；
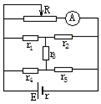
例题4、如图所示的电路中，如滑动变阻器接入电路的阻值分别取R1＝2.5Ω,R2=4.5Ω时，电流表的示数分别为I1＝1A，I2＝0.6A，为使电流表示数I3＝0.5A，则滑动变阻器接入电路的阻值应取R3＝？
例题5、用网球拍以速度v击打以速度v0迎面飞来的网球，则被打击后的网球飞回的速率最大不会超过＿＿＿＿＿＿。
例题6、如图所示，质量为m，长为L的均匀金属棒MN，通过两根金属丝悬挂在绝缘支架的P、Q两点上，P与Q间又和充电至电压为U0的电容器相连，电容为C。整个装置处在方向竖直的匀强磁场中，磁感应强度为B，接通电键S，设在极短的时间内电容器放电完毕后立即断开电键，则金属棒MN能摆起的最大高度H＝＿＿＿＿＿＿＿；若接通电键S后在极短的时间内便断开，发现金属棒MN所能摆起的最大高度只有h=H/2，则此时电容器两极间的电压为U＝＿＿＿＿＿＿＿。
例题7、竖直上抛一个小球，空气阻力不计，g取10m/s2，若前5s内小球通过的路程为65m，则小球的初速度大小可能为：（ ）
A、38m/s； B、30m/s； C、25m/s； D、20m/s；
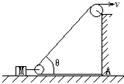
例题8、如图所示，绳头被拉着向右以速度v做匀速运动，当倾斜绳与水平线夹角为θ时，物体M沿水平面运动的速度为多大？
专题训练一
一、选择题
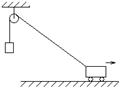1、如图所示，当小车沿水平面向右匀速运动时，绳中拉力大小F与重物的重力大小G间的关系为：（ ）
A、F＞G； B、F＝G； C、F＜G； D、无法确定；
2、如图所示，物块穿在水平杆上，绳的一端系在物块上，另一端穿过定滑轮，大小恒定的拉力F作用于绳端，把物块从a点拉到b点时，拉力做功W1，把物块从b点拉到c点时，拉力F做功W2，若ab=bc，则：（ ）
A、W1＞W2； B、W1＝W2； C、W1＜W2； D、无法确定；
3、手榴弹在空中飞行，当速度方向水平时，其动能为800J，若此时炸裂成质量相等的两块，其中一块的动能为625J，则另一块的动能可能为：（ ）
A、200J； B、300J； C、4000J； D、6000J；
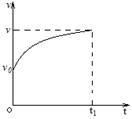
4、如图所示的是质点沿直线运动时速度随时间变化的曲线，在t1时间内速度从v0变为v，则这段时间内平均速度可能为：（ ）
A、
； B、
C、
； D、无法确定；
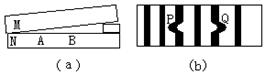
5、如图a所示，用单色光照射透明标准板M来检查零件N的表面情况，观察到如图b所示的条纹，P和Q说明：（ ）
A、N的表面A处向上凸起； B、N的表面B处向上凸起；
C、N的表面A处向上凹起； D、N的表面B处向下凹起；
二、填空题
6、如图所示，长为l的绝缘线把小球A悬于O点，另一小球B被固定在O点正下方l。使两小球带同种电荷，平衡时悬线与竖直方向夹角为θ1，悬线中张力大小为F1；若两小球带电量均减少，再次平衡时悬线与竖直方向夹角为θ2，悬线中张力大小为F2，则应有：θ1＿＿＿＿θ2；F1＿＿＿＿F2。.
7、如图所示，已知R1＝12Ω，其余电阻的阻值均相同，测得A与B间总电阻为4Ω，今将R1换成另一个阻值为R2＝6Ω的电阻，则A与B间的总电阻为＿＿＿＿Ω。
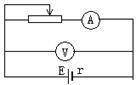8、如图所示的是测量电池电动势和内电阻的电路，测量的原理是：利用电流表测量干路电流I，利用电压表测量路端电压U，根据闭合电路欧姆定律即可得电池的电动势和内电阻。但由于电压表的分流，使得电流表所测得的电流实际上并还是干路电流，若电压表内阻为RV，电流表内阻为RA，电池电动势与内电阻的真实值分别为E和r，
则其测量值分别为
。
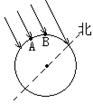9、摆长为L，摆球质量为m的单摆做小角度摆动时最大速度为v，则在半个周期内，回复力对时间的平均值最小为＿＿＿＿；最大为＿＿＿＿＿。
10、古希腊地理学家通过长期观察，发现6月21日正午时刻，在北半球A城阳光与竖直方向成7.5°角向下射，而在A城正南方，与A城之间的地面距离为L的B城，阳光恰好沿竖直方向向下射，如图所示，射到地球的太阳光可视为平行光。据此可估算出地球的半径。试写出估算地球半径的表达式R＝＿＿＿＿＿＿＿＿。
三、计算题
11、质点做匀减速直线运动，第1s内位移大小为10m，停止前进前的最后1s内位移大小为2m，则质点运动的初速度和加速度分别为多大？
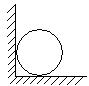
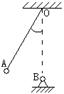
12、如图所示，若水平地面粗糙而竖直墙壁光滑，均匀的球静止于墙角，试分析球的受力情况。
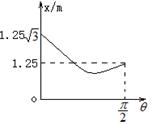
13、物体以一定初速度
沿斜面向上运动，所能达到的最大位移
与斜面倾角θ的关系如图所示，取重力加速度g=10m/s2，试求：当θ为多大时，x的值最小。
14、某质点从静止开始做匀加速直线运动，当速度为v时又立即做匀减速直线运动至静止，若这过程中质点通过的总位移为S，则所经历的时间为多长？
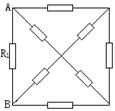
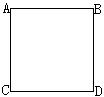15、如图所示中A、B、C、D是匀强电场中一正方形的四个顶点，已知A、B、C三点的电势分别为UA＝15V，UB＝3V，UC＝－3V，求D点的电势。
16、如图所示，半径为R的圆环形导线内通以强度为I的电流，电流为逆时针方向，当圆环形通电导线处在磁感应强度为B，方向垂直于环面的匀强磁场中时，圆环形导线中的张力大小为多少？
17、质点沿直线运动，初速度为v1，受到大小为I的合外力冲量作用后，末速度为v2，则这过程中质点的动能增量ΔEk＝？
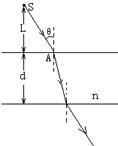
18、在折射率为n，厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以角度θ入射到玻璃板上表面，经过玻璃板后从下表面射出，如图所示。若沿此线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等，点光源S到玻璃板上表面的垂直距离L应是多少？