专题三、带电粒子的运动-高中三年级物理试题练习、期中期末试卷、测验题、复习资料-高中物理试卷-试卷下载

专题三、带电粒子的运动

分析带电粒子在电场、磁场中运动，主要是两条线索：

（1）力和运动的关系。根据带电粒子所受的力，运用牛顿第二定律并结合运动学规律求解。

（2）功能关系。根据场力及其它外力对带电粒子做功引起的能量变化或全过程中的功能关系，从而可确定带电粒子的运动情况，这条线索不但适用于均匀场，也适用于非均匀场。因此要熟悉各种力做功的特点。

【例1】（2004天津理综）钍核发生衰变生成镭核并放出一个粒子。设该粒子的质量为、电荷量为q，它进入电势差为U的带窄缝的平行平板电极和间电场时，其速度为，经电场加速后，沿方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场，垂直平板电极，当粒子从点离开磁场时，其速度方向与方位的夹角，如图所示，整个装置处于真空中。

（1）写出钍核衰变方程；

（2）求粒子在磁场中沿圆弧运动的轨道半径R；

（3）求粒子在磁场中运动所用时间。

解析：（1）钍核衰变方程　 ①

（2）设粒子离开电场时速度为，对加速过程有　②

粒子在磁场中有　　　　　　　　　　③

由②、③得　　　　　　　　　④

（3）粒子做圆周运动的回旋周期⑤

粒子在磁场中运动时间　　　　　　　　　⑥　　　　　　　　　

由⑤、⑥得　　　　　　　　　　　　　　⑦

【例2】（2004湖南理综）如图所示，在y＞0的空间中存在匀强电场，场强沿y轴负方向；在y＜0的空间中，存在匀强磁场，磁场方向垂直xy平面（纸面）向外。一电量为q、质量为m的带正电的运动粒子，经过y轴上y＝h处的点P₁时速率为v₀，方向沿x轴正方向；然后，经过x轴上x＝2h处的 P₂点进入磁场，并经过y轴上y＝处的P₃点。不计重力。求

（l）电场强度的大小。

（2）粒子到达P₂时速度的大小和方向。

（3）磁感应强度的大小。

解析：（1）粒子在电场、磁场中运动的轨迹如图所示。设粒子从P₁到P₂的时间为t，电场强度的大小为E，粒子在电场中的加速度为a，由牛顿第二定律及运动学公式有

qE ＝ ma　　　　　　　　　　　　 ①

v₀t ＝ 2h　　　　　　　　　　　　 ②

　　　　　　　　　　　　 ③

由①、②、③式解得　　　　　　　　④

（2）粒子到达P₂时速度沿x方向的分量仍为v₀，以v₁表示速度沿y方向分量的大小，v表示速度的大小，θ表示速度和x轴的夹角，则有

　　　　　　　　　　 ⑤

　　　　　　　　 ⑥

　　　　　　　　　　 ⑦

由②、③、⑤式得

v₁＝v₀　　　　　　　　　　　　　 ⑧

由⑥、⑦、⑧式得

　　　　　　　　　　　 ⑨

　　　　　　　　　　　　 ⑩

（3）设磁场的磁感应强度为B，在洛仑兹力作用下粒子做匀速圆周运动，由牛顿第二定律　　　　　　　　　　　　　　　　　　　 ⑾

r是圆周的半径。此圆周与x轴和y轴的交点分别为P₂、P₃。因为OP₂＝OP₃，θ＝45°，由几何关系可知，连线P₂P₃为圆轨道的直径，由此可求得

r＝　　　　　　　　　　　　　 ⑿

由⑨、⑾、⑿可得　　　　　　　　　　　　　　 ⒀

【例3】（2004北京理综）如图所示，正方形区域abcd中充满匀强磁场，磁场方向垂直纸面向里。一个氢核从ad边的中点m沿着既垂直于ad边又垂直于磁场的方向，以一定速度射入磁场，正好从ab边中点n射出磁场。若将磁场的磁感应强度变为原来的2倍。其他条件不变，则这个氢核射出磁场的位置是　（答案：C ）

A．在b、n之间某点　　 B．在n、a之间某点

C．a点　　　　　　　　 D．在a、m之间某点

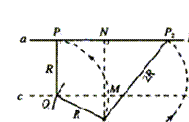
【例4】（2004广东）如图，真空室内存在匀强磁场，磁场方向垂直于纸面向里，磁感应强度的大小B=0.60T，磁场内有一块平面感光板ab，板面与磁场方向平行，在距ab的距离处，有一个点状的放射源S，它向各个方向发射粒子，粒子的速度都是，已知粒子的电荷与质量之比，现只考虑在图纸平面中运动的粒子，求ab上被粒子打中的区域的长度。

解析：粒子带正电，故在磁场中沿逆时针方向做匀速圆周运动，

用R表示轨道半径，有　 ①

文本框: 由此得

代入数值得R=10cm　　可见，2R>l>R.

因朝不同方向发射的粒子的圆轨迹都过S，由此可知，某一圆轨迹在图中N左侧与ab相切，则此切点P₁就是粒子能打中的左侧最远点.为定出P₁点的位置，可作平行于ab的直线cd，cd到ab的距离为R，以S为圆心，R为半径，作弧交cd于Q点，过Q作ab的垂线，它与ab的交点即为P₁.　　　　②

再考虑N的右侧。任何粒子在运动中离S的距离不可能超过2R，以2R为半径、S为圆心作圆，交ab于N右侧的P₂点，此即右侧能打到的最远点.

由图中几何关系得　　　③

所求长度为　　　④　　　代入数值得 P₁P₂=20cm　　 ⑤

【例5】如图甲所示，一对平行放置的金属板M、N的中心各有一小孔P、Q，PQ连线垂直金属板；N板右侧的圆A内分布有方向垂直于纸面向外的匀强磁场，磁感应强度大小为B，圆半径为r，且圆心O在PQ的延长线上。现使置于P处的粒子源连续不断地沿PQ方向放出质量为m、电量为＋q的带电粒子（带电粒子的重力和初速度忽略不计，粒子间的相互作用力忽略不计），从某一时刻开始，在板M、N间加上如图乙所示的交变电压，周期为T，电压大小为U。如果只有在每一个周期的0―T/4时间内放出的带电粒子才能从小孔Q中射出，求：

（1）在每一个周期内哪段时间放出的带电粒子到达Q孔的速度最大？

（2）该圆形磁场的哪些地方有带电粒子射出，在图中标出有带电粒子射出的区域。

解析：（1）在每一个周期内放出的带电粒子到达Q孔的速度最大。设最大速度为v，则据动能定理得，

求得。

（2）因为，解得带电粒子在磁场中的最小

偏转角为。　所以图中斜线部分有带电粒子射出。

【例6】如图（1）所示，虚线上方有场强为E的匀强电场，方向竖直向下，虚线上下有磁感应强度相同的匀强磁场，方向垂直纸面向外，a b是一根长的绝缘细杆，沿电场线放置在虚线上方的场中，b端在虚线上，将一套在杆上的带正电的小球从a端由静止释放后，小球先作加速运动，后作匀速运动到达b端，已知小球与绝缘杆间的动摩擦系数μ＝0.3，小球重力忽略不计，当小球脱离杆进入虚线下方后，运动轨迹是半圆，圆的半径是/3，求带电小球从a到b运动过程中克服摩擦力所做的功与电场力所做功的比值。

解析：从分析带电小球在绝缘杆上运动时的受力情况入手，由最终小球运动的平衡方程求出电场力与洛仑兹力大小的关系。再由磁场中所作R＝/3的圆周运动列出动力学方程，求出小球从b端飞出时速度大小。小球从a到b运动过程中受的摩擦力是变力，可以由动能定理求出其所做功的值。

解析： ①小球在沿杆向下运动时，受力情况如图（2），向左的洛仑兹力F，向右的弹力N，向下的电场力qE，向上的摩擦力f。

F＝Bqv，N＝F＝Bqv₀

∴f＝μN＝μBqv

当小球作匀速运动时，qE＝f＝μBqv₀

②小球在磁场中作匀速圆周运动时，

又　　　　　 ∴v_b＝Bq/3m

③小球从a运动到b过程中，由动能定理得　　

所以　　　　　

【例7】如图所示，固定的半圆弧形光滑轨道置于水平方向的匀强电场和匀强磁场中，轨道圆弧半径为R，磁感应强度为B，方向垂直于纸面向外，电场强度为E，方向水平向左。一个质量为m的小球（可视为质点）放在轨道上的C点恰好处于静止、圆弧半径OC与水平直径AD的夹角为α(sinα=0.8)。

（1）求小球带何种电荷，电荷量是多少？并说明理由。

（2）如果将小球从A点由静止释放，小球在圆弧轨道上运动时，对轨道的最大压力的大小是多少？

解析：（1）小球在C点受重力、电场力和轨道的支持力处于平衡，电场力的方向一定是向左的，与电场方向相同，如图所示。因此小球带正电荷。

（2）小球从A点释放后，沿圆弧轨道滑下，还受方向指向轨道的洛伦兹力f，力f随速度增大而增大，小球通过C点时速度（设为v）最大，力f最大，且qE和mg的合力方向沿半径OC，因此小球对轨道的压力最大。

由　　②

通过C点的速度

球在重力、电场力、洛伦兹力和轨道对它的支持力作用下沿轨道做圆周运动，有

　 ③

最大压力的大小等于支持力

【例8】如图18所示，与纸面垂直的竖直面MN的左侧空间中存在竖直向上场强大小为E=2.5×10²N/C的匀强电场（上、下及左侧无界）。一个质量为m=0.5kg、电量为q=2.0×10^—2C的可视为质点的带正电小球，在t=0时刻以大小为V₀的水平初速度向右通过电场中的一点P，当t=t₁时刻在电场所在空间中加上一如图19所示随时间周期性变化的磁场，使得小球能竖直向下通过D点，D为电场中小球初速度方向上的一点，PD间距为L，D到竖直面MN的距离DQ为L/π。设磁感应强度垂直纸面向里为正。（g=10m/s²）

（1）如果磁感应强度B₀为已知量，试推出满足条件时t₁的表达式（用题中所给物理量的符号表示）。

（2）若小球能始终在电场所在空间做周期性运动。则当小球运动的周期最大时，求出磁感应强度B₀及运动的最大周期T的大小。

解析：当小球进入电场时：mg=Eq将做匀速直线运动

（1）在t₁时刻加入磁场，小球在时间t₀内将做匀速圆周运动，圆周运动周期为T₀

若竖直向下通过D点，由图甲1分析可知必有以下两个条件：

t₀=3T₀/4　…………2分

PF－PD=R　即：　V₀t₁－L=R　

qV₀B₀=mV₀²/qB₀　

所以：V₀t₁－L=mV₀/qB₀　　

t₁=L/V₀+m/qB₀

（2）小球运动的速率始终不变，当R变大时，T₀也增加，小球在电场中的运动的周期T增加，

在小球不飞出电场的情况下，当T最大时有：

DQ=2R　　L/π=2mV₀/qB₀　　

B₀=2πmV₀/qL

T₀=2πR/V₀=2πm/qB₀=L/V₀

由图分析可知小球在电场中运动的最大周期：

T=8×3T₀/4=6L/V₀

【例9】如图所示，在一个光滑绝缘足够长的水平面上，静置两个质量均为m，相距l的大小相等的可视为质点的小球，其中A球带正电，电荷量为q，B球不带电。现在水平面上方加上一个场强大小为E，方向沿AB连线方向水平向右的匀强电场，匀强电场充满水平面上方的整个空间。在电场力作用下，A球沿水平面向右运动并与B球发生碰撞，碰撞中A、B两球无动能损失且无电荷转移，两球碰撞时间极短。求

（1）A、B两球第一次碰撞前A球的速度v_A1;

（2）A、B两球第一次碰撞后B球的速度v′_B1；

（3）两球第一次碰撞后，还会再次不断发生碰撞，且每次碰撞后两球都交换速度，则第一次碰撞结束到第二次碰撞前的时间间隔△t₁和第二次碰撞结束到第三次碰撞前的时间间隔△t₂之比为多少？

解析：（1）第一次碰撞前，电场力对A球做正功，由动能定理得

　　　 ①

　（2）A、B两球第一次碰撞过程中，动量守恒和总动能守恒，则

　　　　　　　　 ②

　　　　　 ③

由②、③解得 ④

　（3）第二次碰撞前，设A球速度为v_A₂，A球为为追上B球与它发生碰撞应满足

　　　　　⑤

　　　　对A球由动量定理得qE△t₁=mv_A2－mv′_A1　 ⑥

第二次碰撞后，A、B两球交换速度，

v′_A2 = v′_B1= v_A1，v′_B2= v_A2=2 v_A1　　　　　　　⑦

第三次碰撞前，设A球速度为v_A₃，A球为追上B球与它生生碰撞应满足

　　　　　 ⑧

由⑦、⑧得v_A3=3v_A1　　　　　　　　 ⑨　

对A球由动量定理得　 qE△t₂=mv_A₃－mv′_A₂　 ⑩

由④⑤⑥⑦⑨⑩得　　　　　　　　11

【例10】在水平桌面上有一矩形真空管，管内O点（O点在真空管的上表面上）的正下方有一阴极射线源A，阴极射线源A连续发射速度大小和方向均不变的电子束.实验要求测A至O点的距离，当在真空管内加互相垂直的匀强电磁场时，电场强度的方向竖直向下，磁场方向垂直纸面向里，电子束沿水平方向做匀速直线运动.当在真空管内部只加前述的匀强电场而不加磁场时，电子束沿水平方向做匀速直线运动.当在真空管内部只加前述的匀强电场而不加磁场时，电子束打在真空管上表面的C点，测得OC之间的距离为，当在真空管内只加与前述磁感应强度大小相同、方向相反的匀强磁场而不加电场时，电子束打在真空管上表面的D点，测得OD之间的距离为，求A点到O点的距离.

解析：电子束沿水平方向做匀速直线运动时：

　　　　　　　　　　　 ……①

　　　当只有电场存在时：　 l₁=v·t……②

　　　　　　　　　　　 ……③

只有磁场时：……④　　由几何关系可知：…⑤

　　　由①~⑤式解得：

【例11】如图所示，一束波长为λ的强光射在金属板P的A处发生了光电效应，能从A处向各个方向逸出不同速率的光电子。金属板P的左侧有垂直纸面向里的匀强磁场，磁感强度为B，面积足够大，在A点上方L处有一涂荧光材料的金属条Q，并与P垂直。现光束射到A处，金属条Q受到光电子的冲击而发出荧光的部分集中在CD间，且，光电子质量为m，电量为e，光速为c，

　（1）金属板P逸出光电子后带什么电？

　（2）计算P板金属发生光电效应的逸出功W。

　（3）从D点飞出的光电子中，在磁场中飞行的最短时间是多少？

解析：（1）由电荷守恒定律得知P带正电　

　（2）所有光电子中半径最大值　

逸出功　　

（3）以最大半径运动并经B点的电子转过圆心角最小，运动时间最短

　　　且　所以

【例12】如图甲所示，A、B两块金属板水平放置，相距为d=0．6cm，两板间加有一周期性变化的电压，当B板接地(=0)时，A板电势随时问变化的情况如图乙所示，现有一带负电的微粒在t=0时刻从B板中央小孔射入电场，若该带电微粒受到的电场力为重力的两倍，且射入电场时初速度可忽略不计。求：

　（1）在0～和～ T这两段时间内微粒的加速度大小和方向；

　（2）要使该微粒不与A板相碰，

所加电压的周期最长为多少?(g=10m／s²)

解析：（1）设电场力大小为F，则F=2mg

　　对于t=0时刻射入的微粒，在前半个周期内，

方向向上　　　　　　

后半个周期的加速度a₂满足

方向向下　　　　　　　　　　

（2）前半周期上升的高度.前半周期微粒的末速度为

后半周期先向上做匀减速运动，设减速运动时间为t₁，则

此段时间内上升的高度

则上升的总度高为　　　　　　　　　

后半周期的时间内，微粒向下加速运动.

下降的高度　　　　　　　　　　　　　　　　

上述计算表明，微粒在一个周期内的总位移为零，只要在上升过程中不与A板相碰即可，则

所加电压的周期最长为　　

【例13】在直径为d的圆形区域内存在均匀磁场，磁场方向垂直于圆面指向纸外。一电量为q。质量为m的粒子，从磁场区域的一条直径AC上的A点射入磁场，其速度大小为v₀，方向与AC成α角。若此粒子恰好能打在磁场区域圆周上的D点，AD与AC的夹角为β，如图所示，求该匀强磁场的磁感应强度B的大小。

解析：一带正电的小球质量为m=1×10^－2kg, 带电量为q=1×10^－2C，小球在相互垂直的均强电场和匀强磁场的空间中沿一斜线向下做匀速直线运动。如图所示，已知其水平分速度为v_x=6m/s，磁感应强度大小为B=1T，方向垂直纸面向里，电场力做负功的功率大小为P_E=0.3W。试求：电场强度大小和方向。（g取10m/s²，方向可用反三角函数表示）。

解析：设粒子在磁场中圆周运动半径为R，其运动轨迹如图所示，O为圆心，则有：

　　　 ①　

　　又设AO与AD的夹角为γ，由几何关系知：

　　可得：　⑤

　　代入①式得：　⑥（

【例14】如图所示，在竖直平面内建立xOy直角坐标系，Oy表示竖直向上的方向。已知该平面内存在沿x轴负方向的区域足够大的匀强电场，现有一个带电量为2.5×10^－4C的小球从坐标原点O沿y轴正方向以0.4kg.m/s的初动量竖直向上抛出，它到达的最高点位置为图中的Q点，不计空气阻力，g取10m/s².

　（1）指出小球带何种电荷；

　（2）求匀强电场的电场强度大小；

　（3）求小球从O点抛出到落回x轴的过程中电势

能的改变量.

解析：（1）小球带负电

（2）小球在y方向上做竖直上抛运动，在x方向做初速度为零的匀加速运动，

最高点Q的坐标为（1.6m, 3.2m）　由 ①　

代入数据得　（1分）由初动量p=mv₀　②　

解得 m=0.05kg　　又 ③　

④　　由③④代入数据得E=1×10³N/C　

（3）由④式可解得上升段时间为t=0.8s　

所以全过程时间为　

代入③式可解得x方向发生的位移为x=6.4m　

由于电场力做正功，所以电势能减少，设减少量为△E，代入数据得△E=qE_x=1.6J

【例15】如图所示，真空室内，在d≤x≤2d的空间中存在着沿+y方向的有界匀强电场，电场强度为E；在－2d≤x≤－d的空间中存在着垂直纸面向里的有界匀强磁场，磁场强度为B。在坐标原点处有一个处于静止状态的原子核，某时刻该原子核经历一次衰变，沿+x方向射出一质量为m、电荷量为q为粒子；质量为M、电荷量为Q的反冲核进入左侧的匀强磁场区域，反冲核恰好不从磁场的左边界射出。如果衰变过程中释放的核能全部转化为粒子和反冲核的动能，光速为c，不计粒子的重力和粒子间相互作用的库仑力。求：

　　（1）该核衰变过程中的质量亏损△m；

　　（2）粒子从电场右边界射出时的坐标。

解析：（1）依据题意知反冲核在磁场中做匀速圆周运动的半径为d，设原子核衰变后M、m的速度分别为v₁、v₂

根据牛顿第二定律为

衰变过程中M、m系统满足动量守恒定律：Mv₁－mv₂=0

衰变后反应总动能为

根据质能方程有：E_k=△mc²

联立解得：

　（2）设m进入电场运动过程中，沿电场方向偏转的距离为y，则有

m的加速度为

m在电场中运动的时间为

联立得：

所以坐标为：

【例16】显像管的工作原理是阴极K发射的电子束经高压加速电场（电压U）加速后垂直正对圆心进入磁感应强度为B、半径为r的圆形匀强偏转磁场，磁场右端Q点到荧光屏的距离为l，如图所示，偏转后轰击荧光屏P，荧光粉受激而发光，在极短时间内完成一幅扫描。若去离子水质不纯，所生产的阴极材料中会有少量SO，SO打在屏上出现暗斑，称为离子斑，如发生上述情况，[电子质量为9.1×10^－31kg，硫酸根离子（SO）质量为

　　1.6×10^－25kg，不计重力].

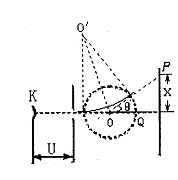
　　（1）试推导电子偏转后射到荧光屏上偏离荧光屏中心的距离的表达式

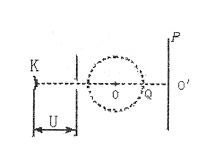文本框: 　　（2）试求分析说明暗斑集中在荧光屏中央的原因

解析：（1）粒子（电子）在加速电场中加速　

　　粒子垂直进入磁场做匀速圆周运动，设轨道半径为R。

文本框: 　

设粒子在偏转磁场中速度偏转角为θ，有：

　　如图所示有

　　（2）由（1）式可知：

　　由于硫酸根离子荷质比远小于电子的荷质比，高速硫酸根离子经过磁场几乎不发生偏转，而集中打在荧光屏中央，形成暗斑

【例17】如图所示，坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场，y轴为两种场的分界面，图中虚线为磁场区域的右边界，现有一质量为m，电荷量为－q的带电粒子从电场中坐标位置（－l，0）处，以初速度v₀，沿x轴正方向开始运动，且已知。试求：使带电粒子能穿越磁场区域而不再返回电场中，磁场的宽度d应满足的条件。

解析：带电粒子在电场中做类平抛运动，设运动的加速度为a，由牛顿运动定律得：

　　qE=ma

　　设粒子出电场、入磁场时速度的大小为v，此时在y轴方向的分速度为v_y，粒子在电场中运动的时间为t，则有：

　　v_y=at

文本框: ( 　　l=v₀t

　解得：v_y=v₀　 v=

　设v的方向与y轴的夹角为θ。则有：

粒子进入磁场后洛仑兹力作用下做圆周运动，如图所示，则有：

由图中的几何关系可知，要使粒子穿越磁场区域，磁场的宽度条件为：

d<R(1+cosθ)

结合已知条件，解以上各式可得

【例18】真空中有一半径为R的圆形匀强磁场区域，磁场方向垂直纸面向外，OX为边界上O点的切线，如图所示，从O点在纸面内向各方向发射速率均为V的粒子，设粒子间相互作用力和重力都忽略，且粒子在磁场中偏转半径也为R，已知粒子的电量为，质量为m，试回答下列各问：

　（1）速度方向分别与OX方向夹角成30°和90°的的粒子在磁场中运动的时间分别

　　　　是多少？

　（2）所有从磁场边界射出的粒子，速度方向有何特征。（简要说明理由）

　（3）若在OX上距O点L处有一点P（L>2R），请设计一种匀强磁场分布，使得从上述

　　　　磁场边界射出的粒子都能够汇聚到P点.

解析：（1）V；V　（2）与OX平行　（3）以P点正上方距离P点r处为圆心，半径为r，垂直纸面向外的匀强磁场.

【例题3】图为一种质谱仪示意图，由加速电场、静电分析器和　　磁分析器组成．若静电分析器通道的半径为R，均匀辐向电场的场强为E．磁分析器中有垂

直纸面向外的匀强磁场，磁感应强度为B．问：

　　(1)为了使位于A处电量为q、质量为m的离子，从静止开始经加速电场加速后沿图中圆弧虚线通过静电分析器，加速电场的电压U应为多大?

　　(2)离子由P点进入磁分析器后，最终打在乳胶片上的Q点，该点距入射点P多远?若有一群离子从静止开始通过该质谱仪后落在同一点Q，则该群离子有什么共同点?

答案：（1）U=ER/2；（2）该群离子都打在Q点必同带正电荷，且具有相同的荷质比。

练习

1．当带电粒子垂直进入匀强磁场和匀强电场时，称这种场为偏转磁场和偏转电场，下列说法正确的是：　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．要想把速度不同的同种带电粒子分开，既可采用偏转磁场，也可以采用偏转电场

　　　 B．要想把动量相同的质子和粒子分开，只能采用偏转磁场

　　　 C．要想把初速度为零，经同一电场加速后的的质子和粒子分开，既可采用偏转电场，也可采用偏转磁场

D．要想把荷质比不同的粒子（初速度相同）分开，只可采用偏转电场，不可采用偏转磁场

2．（2002年广西、河南、广东卷）在图中虚线所示的区域

存在匀强电场和匀强磁场。取坐标如图。一带电粒子沿

x轴正方向进入此区域，在穿过此区域的过程中运动方

向始终不发生偏转。不计重力的影响，电场强度E和磁

感强度B的方向可能是　　　　　　　　　（　　）

　　　 A． E和B都沿x轴正方向　　　　　 B.　 E沿y轴正向，B沿z轴正向

　　　 C． E沿x轴正向，B沿y轴正向　　　　　　D． E、B都沿z轴正向

5．如图，光滑水平面上带电量为q、质量为m的小球P靠在一劲度系数为k的轻弹簧的右端。现将弹簧向左压缩长度为L后自A点静止释放小球P，小球P运动到B处时恰与静止的不带电的相同小球Q相碰并粘在一起，进入水平向右的匀强电场中。C点右侧是垂直纸面向里的匀强磁场，小球运动到C点时，电场突然变为竖直向上，但大小不变。此后物体开始在竖直平面内作圆周运动，到达最高点时撤去电场，小球正好又落回B点。已知AB=BC=L，弹簧的弹性势能与其形变量x的关系是E_p=，式中k为弹簧的劲度系数。

求：（1）小球的带电性并说明理由

（2）场强E的大小

（3）磁感应强度B的大小。

7．（2002年全国理综卷）电视机的显像管中，电子束的偏转是用磁偏转技术实现的。电子束经过电压为U的加速电场后，进入一圆形匀强磁场区域，如图所示。磁场方向垂直于圆面。磁场区中心为O，半径为r。当不加磁场时，电子束将通过O点而打到屏幕的中心M点。为了让电子束射到屏幕边缘P点，需要加一匀强磁场，使电子束偏转一已知角度，此时磁场的磁感应强度B应为多少？

9．带电量为q的粒子（不计重力），匀速直线通过速度选择器（电场强度为E，磁感应强度为B₁），又通过宽度为l，磁感应强度为B₂的匀强磁场，粒子离开磁场时速度的方向跟入射方向间的偏角为θ，如图所示.试证明：入射粒子的质量m=.

10．某空间存在着一个变化的电场和一个变化的磁场，电场方向向右（如图（a）中由B到C

的方向），电场变化如图（ｂ）中E-t图象，磁感应强度变化如图（c）中B-t图象.在A点，从t=1 s（即1 s）开始，每隔2 s，有一个相同的带电粒子（重力不计）沿AB方向（垂直于BC）以速度v射出，恰能击中C点，若=2d且粒子在AC间运动的时间小于1 s，求

（1）图线上E₀和B₀的比值，磁感应强度B的方向.

（2）若第1个粒子击中C点的时刻已知为（1+Δt）ｓ，那么第2个粒子击中C点的时刻是多少?

参考答案：

1.A2.AB　解析：E和B都沿x轴正方向，由于带电粒子速度与磁感应强度B平行或反向平行，故不受磁场力只受电场力，而不论粒子带何种电荷，电场力与速度均共线，由此知粒子作直线运动，A正确。若E沿y轴正向则电场力沿y轴正向（带正电）或负向（带负电），而B沿z轴正向，则由左手定则知其所受洛仑兹力沿y轴负向（带正电）或正向（带负电），合外力可能为零，故B正确。若E沿z轴正向，则电场力沿z轴正向（带正电）或负向（带负电），B沿y轴正向，则洛仑兹力也沿z轴正向（带正电）或负向（带负电），合力不为零，且与速度不共线，粒子必然发生偏转，故C错。若E、B都沿z轴方向，则电场力也沿z轴方向，而洛仑兹力沿y轴方向，合力不为零，且与速度不共线，粒子必发生偏转，故D错。