关山中学2007届第一轮高三物理单元测试题
机 械 能
一、选择题．每小题3分。共36分。在每小题给出的四个选项中．只有一个选项是符合题目要求的。
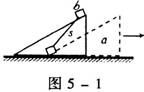1．如图5—1所示，劈α放在光滑的水平面之上，斜面光滑，把b物体
放在光滑的斜面α的顶端，由静止下滑，则在下滑过程中α对b的弹
力对b做功为W1，b对α的弹力对α做功为W2则下列关于W1、W2
的说法中正确的是 ( )
A．W1 = 0 W2 = 0 B．W1 ≠ 0 W2 = 0
C．W1 = 0 W2 ≠ 0 D. W1 ≠ 0 W2 ≠ 0
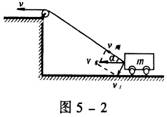
2．如图5—2所示，人用绳通过滑轮在一平台上拉一辆处在平
台下水平地面上的车。设人以速度υ匀速拉绳，那么，当绳
与水平夹角为α，小车的动能为 ( )
A．
B． C． D．
3．下面关于重力势能的说法中，正确的是 ( )
A．有A、B两个物体，A的高度是B高度的2倍，那么物体A的重力势能的数值一定是物体B的2倍
B．从同一高度将某一物体以相同的速度竖直上抛或平抛，从抛出到落地的过程中，物体重力势能的变化是相同的
C．有一物体从楼顶落到地面，如果受到空气阻力，物体重力势能的减小量小于自由下落时重力势能的减小量
D．重力做功时，不仅与物体运动的高度差有关，还与物体运动的路径有关
4．两个质量不同的物体在同一水平面上滑行，物体与水平面间的动摩擦因数相同，比较它们滑行的
最大距离,下列判断中错误的是 ( )
A．若两物体的初速度相等，则它们的最大滑行距离相等
B．若两物体的初动能相等，则它们的最大滑行距离相等
C．若两物体的初动能相等，则质量小的最大滑行距离大
D．若两物体停止前的滑行时间相等，则两物体的最大滑行距离相等
5．一个物体静止在水平面上，现用两种情形对物体施力，使物体在水平面上作直线运动。第一次受
水平力F1作用，第二次受F2作用，且F1 > F2，撤去水平力，物体继续滑行，直到静止，若两次运动总位移相等，FI和F2的冲量分别为，I1和I2，两次作用力所做的功分别为Wl 和W2，那么I1和I2, Wl和W2的大小关系是 ( )
A．I1 = I2 Wl = W2 B． I1 ＜ I2 Wl = W2 C．I1 = I2 Wl ＞W2 D．I1 ＞ I2 Wl ＜W2
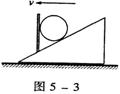6．如图5—3所示,光滑的斜劈放在水平面上,斜面上用固定的竖直
板挡住一个光滑球，当整个装置沿水平面以速度υ匀速运动时，
以下说法中正确的是 ( )
A．小球的重力不做功 B．斜面对球的弹力不做功
C．挡板对球的弹力不做功 D．以上三种说法都正确
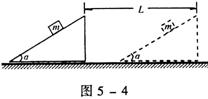
7．有一质量为m的物体始终静止在倾角为α的斜面上，现将斜面在水平面上沿直线匀速向右移动距离L(如图5-4所示)如果斜面作用于m的弹力和摩擦力对m做的功分别形Wl 和W2，则( )
A．W1 = 0 W2 = O
B．W1 = mgLsin2α W2 = mgLcos2α
C．Wl = mgLcos2a W2 = mgLsinαcosα
D．Wl =
mgLsinαcosα W2 = mgLsinαcosα
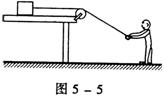
8．如图5-5所示，光滑平台上有一个质量为m的物块，用绳子跨过定滑轮由地面上的人向右拉动，当人以速度υ从平台的边缘处向右匀速前进了s，不计绳和滑轮的质量及滑轮轴的摩擦，且平台离人手作用点竖直高度始终为h，则 ( )
A．在该过程中，物块的运动也是匀速的 B．人对物块做的功为
C．人对物块做的功为
D．物块的运动速率为
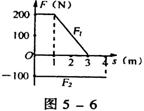
9．某物体同时受到两个在同一直线上的力Fl、F2的作用，物体由静止开始做直线运动,其位移与力Fl、F2的关系图像如图5-6所示,在这4m内，物体具有最大动能时的位移是 ( )
A．1m B．2m C．3m D．4m
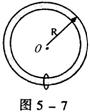10．圆形光滑轨道位于竖直平面内，其半径为R，质量为m的金属小球环套
在轨道上,并能自由滑动，如图5-7所示,以下说法正确的是 ( )
A．要使小圆环能通过轨道的最高点,小环通过最低点时的速度必须大于
B．要使小圆环通过轨道的最高点，小环通过最低时的速度必须大于
C．如果小圆环在轨道最高点时的速度大于 ，则小环挤压轨道外侧
D．如果小圆环通过轨道最高点时的速度大于 ，则小环挤压轨道内侧
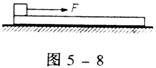11．在光滑水平面上，有一块长木板，长木块左端放一个木块，木块
与长木板间有摩擦，先后两次用相同的水平力F将木块拉离木板，
如图5—8所示，第1次将长木板固定，第2次长木板不固定，比
较这两种情况下，相应的物理量两次相同的应是 ( )
A．木块受到摩擦力的大小不相同
B．恒力F对木块做的功相同
C．因摩擦产生的热相同
D．木块获得的动能相同
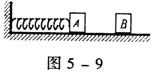12．如图5—9所示,一轻弹簧一端系在墙上,自由伸长时,右端正好
处在B处,今将一质量为m的小物体靠着弹簧，将弹簧压缩到A
处,然后释放,小物体能在水平面上运动到C点静止，AC距离为
s；如将小物体系在弹簧上,在A由静止释放,则小物体将向右运
动,或来回运动后最终停止,设小物体通过的总路程为L ,则下列选项可能的是 ( )
A． L ＞ s B．L = s C．L = 2s D．以上答案都有可能
答 题 卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、实验与填空(4×6=24分)
13．在“验证机械能守恒定律”的实验中：
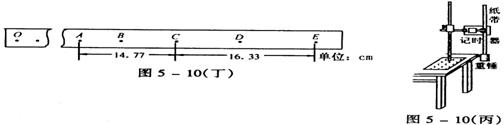①某同学用图5—10(丙)所示装置进行实验，得到如图5—10(丁)所示的纸带。测出点A、C间的距离为14.77cm，点C、E问的距离为16.33cm，已知当地重力加速度为9.8m/s2，重锤的质量为m =1.0kg，则重锤在下落过程中受到的平均阻力大小Fƒ = N．
②某同学上交的实验报告显示重锤的动能略大于重锤的势能，则出现这一问题的原因能是
(填序号)
A．重锤的质量测量错误 B．该同学自编了实验数据
C．交流电源的频率不等于50Hz D．重锤下落时受到的阻力过大
14．物体在水平拉力F作用下沿水平方向做
直线运动，拉力F与时间t的关系和物
体的速度υ，与时间t的关系如图5—11
所示，由图可知，O—7s内拉力对物体做
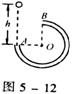的功是 ；拉力在第3s末的功率是 。
15．一根内壁光滑的细圆管，形状如图5—12所示，放在竖直平面内，一个球
自A口的正上方高h处自由下落．第一次小球恰能抵达B点；第二次落入
A口后，自B口射出，恰能再进入A口，则两次小球下的高度之比hl∶h2
。
16．在光滑水平面上有一静止的物体,现以水平恒力甲推该物体,作用一段时间后,换成相反方向的水平恒力乙推该物体,当恒力乙作用时间与恒力甲作用时间相同时,物体恰好回到原处,此时物体的功能为32J,则在整个过程中,恒力甲做的功等于 J，恒力乙做的功等于 J。
三、本题共4小题；40分。解答应写出必要的文字说明、方程式和重要演算步骤。只写出最后
答案的不能得分。有数值计算的题．答案中必须明确写出数值和单位。
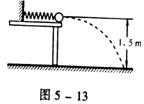17．(8分)如图5—13所示，在高15m的光滑平台上有一个质量为2kg的小球被一细线拴在墙上，球与墙之间有一根被压缩的轻质弹簧，当烧断细线时。小球被弹出，小球落地时的速度方向与水平方向成60°角。求弹簧被压缩时具有的弹性势能．(g = 10m/s2)
18.（10分）一辆质量为5×103kg的汽车，额定功率为60kW,现让汽车保持60kW的功率的水平路面上从静止开始运动，运动中汽车所受阻力恒为车重的0.1倍，求：
（1）启动后0.5s内牵引力做的功；
（2）汽车的加速度为1m/s2时汽车的速度；
（3）汽车的加速度为10m/s时汽车的加速度；
（4）汽车行驶能达到的最大速度（g = 10m/s2）
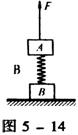
19.（10分）一劲度系数k = 800N/m的轻质弹簧两端分别连接着质量均为12kg的物体A.B,将他们
竖直静止在水平面上，如图5-15所示，现将一竖直向上的变力F作用A上，使A开始向上做匀加速运动，经0.4s物体B刚要离开地面，求：（设整个过程弹簧都在弹性限度内，取g = 10m/s2）
(1)此过程中所加外力F的最大值和最小值；
(2)此过程中力F所做的功
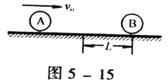20.（12分）在光滑的水平面上轨道上有两个半径都是r的小球A和B,质量分别为m和2m,当两球心间的距离大于L（L比2r大得多）时，两球间无相互作用力；当两球心间的距离等于或小于L时两球间有恒定斥力F设A球从较远处以初速υ0正对静止的B球开始运动（如图5-15），欲使两球不发生接触，υ0必须满足什么条件？
（五）
1．D 2．B 3．B 4．B 5．B 6．A 7．D 8．C 9．B 10．D 11．C 12．B
13．①0.05N ②BC 14．18J、3W 15．4 ：5 16．8J、24J
17．小球落地时的竖直速度 小球落地时的水平速度即离开弹簧时
的速度 由机械能守恒定律可知，原来被压缩时的弹性势能，应等于小球离开弹簧时的动能．即
18．(1)W = Pt = 60×103×0.5 = 3×104J
(2)汽车所受阻力ƒ = 0.1mg = 0.1×5×103×10=5×103N汽车的加速度为1m/s时，设牵引力为
F∴F–ƒ = ma F= ƒ + ma+(5×103×1×5×103)=1.0×104N此时速度υ=P/F=60×103/1.0×104=6m/s
(3)汽车的速度为10m/s时，加速度为
(4)汽车速度最大时,合力为零,牵引力的大小等于阻力,∴汽车的最大速度为υ0=P/ƒ=
19．(1)t = 0时,A所受重力与弹力平衡,此时弹簧的压缩量为 ∴
∴
t = 0.4s时,B受地面支持力为零,此时弹簧的伸长量为
匀加速运动的位移为 外力F最大时，即B刚离地时
(2)过程末了时刻A的速度
在A上升的过程中,弹簧先由压缩 的状态变化为伸长 在上升 阶段，弹力对A作正功,在上升
阶段弹力对A作负功，由对称性可知,在上升阶段弹力所作功的代数和为零,由动能定理有：
 |
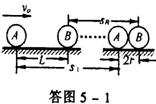20．设两球之间距离从L变化到最小的过程中，它们运动的位移分别为SA、SB (如图答5—1)，相距最近时两球速度分别为 υA 、υB
|
解法一：根据牛顿第二定律，A、B两球运动的
加速度分别为
 |
根据运动学公式有
 |
两球不相接的条件为
由以上六式联立解得
解法二：根据动能定理有
 |
两球不相接触的条件为
由以上三式联立解得
解法三：用相对运动法求解:设A相对B运动,相对初速度为υ0相对末速为零,相对加速度为
相对位移为
根据运动学公式
得