高三物理测试卷：机械能

2005－2006学年度

高三物理测试卷：机 械 能

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。满分150分，考试用时120分钟。

第Ⅰ卷（选择题，共40分）

一、选择题，每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

1．如右图所示，一颗子弹水平射入置于光滑水平面上的木块A并留在A中，A、B用一根轻质弹簧连在一起，则在子弹打击木块及弹簧压缩的整个过程中，对子弹、两木块和弹簧组成的系统　　　　　　　　　　　　　　　　　 （　　）

　　　A．动量守恒，机械能也守恒

A

B

　　　B．动量守恒，机械能不守恒

C．动量不守恒，机械能守恒

D．无法判断动量、机械能是否守恒

2．如图所示，物体以100J的初动能从斜面底端向上运动，当它通过斜面某一点M时，其动能减少80J，机械能减少32J，如果物体能从斜面上返回底端，则物体到达底端时的动能为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．20J　　　　　　　　　　　 B．48J

　　　C．60J　　　　　　　　　　　 D．68J

3．某人用手将1Kg物体由静止向上提起1m，这时物体的速度为2m/s（g取10m/s²），则下列说法正确的是　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　A．手对物体做功12J　　　　　　  　　　B．合外力做功2J

　　　C．合外力做功12J　　　　　　　  　　　D．物体克服重力做功10J

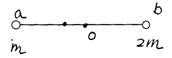
4．如右图所示，在两个质量分别为m和2m的小球a、b间，用一根长为L的轻杆连接，两小球可绕杆的中点O无摩擦地转动，现使杆由水平位置无初速地释放，在杆转动至竖直位置的过程中，下列说法错误的是　　　　　　　　　　 （　　）

　　　A．b球的重力势能减少，动能增加，机械能守恒

　　　B．杆对a球的弹力对a球做正功

　　　C．a球的机械能增加

　　　D．a球和b球组成的系统总机械能守恒

5．利用能量间相互转化，可以储存能量。如图为抽水蓄能电站示

意图，它可调剂电力供应，深夜用电低谷时，用过剩电能把下蓄水

池的水抽到高处的水库内，用电高峰时，则通过闸门放水发电以补

充电能不足。若水库面积为1.2×10⁶m²，抽水机每天从深夜11时

至清晨4时抽水使水库水面增高1m，而抽水过程中水上升高度近

似看成保持为10m不变，若抽水机工作效率为80％，则所有抽水机

抽水总功率为(g=10m/s²，ρ(水)=10³Kg/m³)（　　）

　　　A．6.7×10⁶W　　 　B．8.3×10⁶W　　　C．10⁸W　　 　　　　　 D．10⁷W

6．如图所示，在光滑水平面上紧挨着放置A、B二物块，一颗子弹沿水平直线射穿物块A并进入物块B，最后留在物块B内，设子弹在两物块内运动时所受阻力大小恒定。已知：A、B二物块的质量分别为M_A和M_B，子弹的质量为m；子弹进入物块A时，其速度为v₀；两物块分离时A已移动的距离为S₁，B继续移动距离S₂后子弹与物块B相对静止；物块A和B的长度均为L，根据上述已知条件　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　A．可以求得物块A和B的最后速度v_A和v_B

B

A

B．可以求得子弹在两物块内运动所受阻力

　　　C．可以求得子弹在物块B内进入的深度

　　　D．不可以求出子弹在物块B内进入的深度

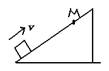
7．下列四个选项的图中，木块均在固定的斜面上运动，其中图A、B、C中的斜面是光滑的，图D中的斜面是粗糙的，图A、B中的F为木块所受的外力，方向如图中箭头所示，图A、B、D中的木块向下运动，图C中的木块向上运动，在这四个图所示的运动过程中机械能守恒的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

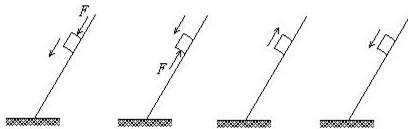
　　A　　　　　　  B　　　　　  C　　　　　　　  D

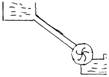
8．水平传送带匀速运动，速度大小为v，现将一小工件放到传送带上。设工件初速为零，当它在传送带上滑动一段距离后速度达到v而与传送带保持相对静止。设工件质量为m，它与传送带间的滑动摩擦系数为μ，则在工件相对传送带滑动的过程中　　　　　 (　　)

　 A．滑摩擦力对工件做的功为mv²／2

　　　B．工件的机械能增量为mv²／2

　　　C．工件相对于传送带滑动的路程大小为v²／2μg

　　　D．传送带对工件做为零

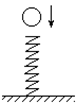
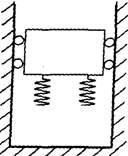9．一升降机在箱底装有若干个弹簧，设在某次事故中，升降机吊　索在空中断裂，忽略摩擦力，则升降机在从弹簧下端触地后直到最低点的一段运动过程中，　　　（　　）

　　　A．升降机的速度不断减小

　　　B．升降机的加速度不断变大

　　　C．先是弹力做的负功小于重力做的正功，

然后是弹力做的负功大于重力做的正功

　　　D．到最低点时，升降机加速度的值一定大

于重力加速度的值。

10．如下图所示，小球从高处下落到竖直放置的轻弹簧上，在将弹簧压缩到最短的整个过程中，下列关于能量的叙述中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A．重力势能和动能之和总保持不变

　　　B．重力势能和弹性势能之和总保持不变

　　　C．动能和弹性势能之和总保持不变

　　　D．重力势能、弹性势能和动能之和总保持不变

第Ⅱ卷（非选择题 共110分）

二、本题共三小题。把答案填在题中的横线上或按题目要求作图

11．在“验证机械能守恒定律”的实验中，已知打点计时器所用的电源频率为50Hz，查得当地的重力加速度为g=9.80m/s²,测得所用重物的质量为1.00kg，实验中得到一条点迹清晰的纸带，如图所示，把第一个点记作O ，另选取连续的4个点A、B、C、D作为测量的点，经测量知道A、B、C、D各点到O点的距离分别为62.99cm,70.18cm,77.76cm.85.73cm,根据以上数据，可知重物由O点运动到C点，重力势能的减少量等于____J，动能的增加量等于____J（取三位有效数字）（8分）

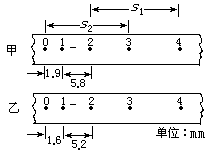
12．在利用自由落体运动验证机械能守恒定律的实验中，(1)若应用公式v=gt计算即时速度进行验证，打点计时器所接交流电的频率为50赫兹，甲、乙两条实验纸带，如图所示，应选________纸带好.（6分）

13．若通过测量纸带上某两点间距离来计算即时速度，进行验证，设已测得点2到4间距离为s₁,点0到3间距离为s₂ ，打点周期为T，为验证重物开始下落到打点计时器打下点3这段时间内机械能守恒、实验后，s₁、s₂和T应满足的关系为T=____________.（6分）

三、本题共7小题，90分。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题答案中必须明确写出数值和单位。

14．一辆汽车质量为m，从静止开始起动，沿水平面前进了s米后，就达到了最大行驶速度v_m，设汽车的牵引功率保持不变，所受阻力为车重的k倍。求：

　　　(a)汽车的牵引力功率。

　　　(b)汽车从静止到开始匀速运动所需的时间(提示：汽车以额定功率起动后的运动不是匀加速运动，不能用运动学公式求解)。（10分）

15．如图所示，有光滑圆弧形轨道的小车静止在光滑水平面上，其质量为M，有一质量为m的小球以水平速度v₀沿轨道的水平部分冲上小车.若小球沿圆弧形轨道上升的最大高度为H，在此过程中圆弧形轨道对小球的弹力所做的功为多大？（10分）

16．如图所示，水平放置的轻质弹簧，左端固定，右端与小物块P接触而不连接，当P在A点时，弹簧为原长，现在用水平向左的推力将P物缓慢地从A推到B点，需做功6J，此时在B点撤去推力后，P从静止开始沿着水平桌面滑到停放在水平光滑地面上的小车Q上（小车与桌面等高），已知P的质量m=1Kg，Q的质量M=4Kg，AB间距5cm，AC间距90cm，P与桌面和Q面间摩擦系数μ=0.4，p与BC间光滑，试求：

　　　⑴小车滑到桌面边缘C处的速度？

　　　⑵P不会从Q的右端滑出，则小车Q至少多长？

　　　⑶从推力作用于P到P与Q一起运动的全过程中产生的热量？（12分）

　　　

17．如图所示，质量为M的滑块B套在光滑的水平杆上可自由滑动，质量为m的小球A用一长为L的轻杆与B上的O点相连接，轻杆处于水平位置，可绕O点在竖直平面内自由转动。

　　　⑴固定滑块B，给小球A一竖直向上的初速度，使轻杆绕O点转过90°，则小球初速度的最小值是多少？

　　　⑵若M=2m，不固定滑块B。给小球A一竖直向上的初速度V₀，则当轻杆绕O点转过90°，A球运动至最高点时，B的速度多大？（14分）

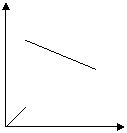
18．如下图所示，质量为M，长L=1.0m，右端带有竖直挡板的木块B，静止在光滑水平面上，一个质量为m的小木块（可视为质点）A，以水平速度v₀=4.0m/s滑到B的左端，而后与右端挡板碰撞，最后恰好滑到木板B的左端。已知M/m=3，并设A与挡板碰撞时无机械能损失，碰撞时间可以忽略，求：

　　　⑴A、B的最后速度。

　　　⑵木块A与木板B间的动摩擦因数。

　　　⑶在图乙所给坐标中画出此过程中B相对地的速度-时间图线。（14分）

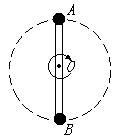
19．如图所示，轻杆长2l，中点装在水平轴O点，两端分别固定着小球A和B，A球质量为m ,B球质量为2m，两者一起在竖直平面内绕O轴做圆周运动。（1）若A球在最高点时，杆A端恰好不受力，求此时O轴的受力大小和方向；（2）若B球到最高点时的速度等于第（1）小题中A球到达最高点时的速度，则B球运动到最高点时，O轴的受力大小和方向又如何？（3）在杆的转速逐渐变化的过程中，能否出现O轴不受力的情况？若不能，请说明理由；若能，则求出此时A、B球的速度大小。（15分）

20．如图所示，球A无初速地沿光滑圆弧滑下至最低点C后，又沿水平轨道前进至D与质量、大小完全相同的球B发生动能没有损失的碰撞。B球用长L的细线悬于O点，恰与水平地面切于D点。A球与水平地面间摩擦系数m=0.1，已知球A初始高度h=2米，CD=1米。问：

　　(1)若悬线L=2米，A与B能碰几次?最后A球停在何处？

　　(2)若球B能绕悬点O在竖直平面内旋转，L满足什么条件时，A、B将只能碰两次？A球最终停于何处？（15分）

　　　　　　　　　　　　 　　　　　　　　　　　　　　　 

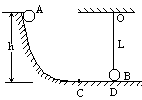
物理参考答案（七）

题号	1	2	3	4	5	6	7	8	9	10
序号	B	A	ABD	CD	B	C	C	ABC	C	D

11．7.62　7.56　　12．(1)甲　　　　13． T=

14．设功率为P　　　 P=F_引V_m　　　　匀速时F_引=kmg　 P= kmgV_m-……5分

 Pt=……2分　 而f= kmg　　 t=……3分

15．水平方向动量守恒　 mv₀=(M+m)v　　　　v=……3分　　对小球应用动能定理

=W_弹+W_重……3分 　W_重=－mgH  W_弹=+mgH……4分

16．（1）W=　　v=2m/s……4分　 (2) mv=(M+m)v_共　

　　----------4分

（3）产生的热量为Q==---------------4分

17．(1)　　v=------------4分　(2)A、B水平方向动量守恒，

A到最高点的速度为V₁滑块的速度为V₂　　m V₁－M V₂=0-　 ---4分

根据能量守恒---------4分解得V₂= -----2分

18．（1）由系统的动量守恒得到　mv₀=(M+m)v　　 v==1m/s　　 向右---------2分

（2）用系统总能量守恒得到　　--------3分

v/m·s－1

(3)设A与B碰前后，A的速度分别为v_A和v_A’　　B的速度分别为V_B和v_B’,根据相碰的过程满足动量和能量守恒得到mv₀=mv_A+MV_B 　　 -------3分

1.7

解得v_A=　　V_B=

0.3

1

v_A’ = 　　 v_B’=

0

0.3

t/s

而后B以1m/s²减速到1m/s－－

则t=1+－1=0.7s-　　  -----3分　　 B的v-t图象如图示　　　　-----3分

19．(1)A在最高点时，对A有mg=m，对B有T_OB-2mg=2m，可得T_OB=4mg。根据牛顿第三定律，O轴所受有力大小为4mg，方向竖直向下 ------------5分 （2）B在最高点时，对B有2mg+ T′_OB=2m，代入（1）中的v，可得T′_OB=0；对A有T′_OA-mg=m, T′_OA=2mg。根据牛顿第三定律，O轴所受的力的大小为2mg，方向竖直向下　　　　　　　　　　　　　　　　　　　　　  ---------------5分

（3）要使O轴不受力，据B的质量大于A的质量，可判断B球应在最高点。对B有T′′_OB+2mg=2m，对A有T′′_OA-mg=m。轴O不受力时，T′′_OA= T′′_OB,可得v′=-　　　　　　　　　　　　　　　  ------5分

20。(1)20次　 A球停在C处　 ------------7分

(2)L£0.76米，A球停于离D9.5米处-　　　　  ------8分