高三物理测试卷：动量

2005－2006学年度

高三物理测试卷：动量

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。共150分考试用时120分钟。

第Ⅰ卷（选择题共40分）

一、每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确。

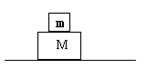
1．如图7-16所示，质量分别为m、M的两物体叠放在水平面上，物体m与物体M间的动摩擦因素为μ₁ , 物体M与水平面间的动磨擦因素为μ₂ ，两物体朝相反方向运动，物体m在物体M上滑动的过程中，正确的说法是　 　　　 （　　）

A．若μ₁≠0　μ₂=0 ，m与M组成的系统动量守恒.

　　　B．若μ₁≠0　μ₂≠0 ，m与M组成的系统动量不守恒.

　　　C．若μ₁=0　 μ₂≠0 ，m与M组成的系统动量守恒.

　　　D．若μ₁=0　μ₂=0 ，m与M组成的系统动量不守恒.

2．质量相同的甲、乙两小球，自同一高度以相同的速率抛出，甲作平抛运动，乙作竖直上抛运动，则在从抛出到落地的过程中 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．两球动量的变化相同.

　　　B．两球所受重力的冲量相同.

　　　C．两球动量的变化不同，乙球动量的变化较大.

　　　D．两球动量的变化率相同.

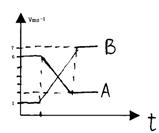
3．一个小孩在蹦床上做游戏，他从高处落到蹦床上又被弹起原高度，小孩从高处开始下落到弹回的整个过程中，他的运动速度随时间变化的图象如图所示，图中oa段和cd段为直线，则根据此图象可知，小孩和蹦床相接触的时间为　　　 （　　）

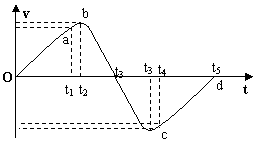
　　　A．t₂~t₄　　　　　　　　　　 B．t₁~t₄

　　　C．t₁~t₅　　　　　　　　　　 D．t₂~t₅

4．在质量为M的小车中挂有一单摆，摆球的质量为m₀，小车和单摆一起以恒定的速度v沿

　 光滑水平面运动，与位于正对面的质量为m的静止木块发生碰撞，碰撞的时间极短，在此碰撞过程中，下列哪个说法是可能发生的　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　A．小车、木块、摆球的速度都发生变化，分别变为v₁、v₂、v₃，满足(M＋m)v=Mv₁＋mv₂＋m₀v₃

　　　B．摆球的速度不变，小车和木块的速度分别变为v₁和v₂，满足Mv=Mv₁＋mv₂

　　　C．摆球的速度不变，小车和木块的速度都变为v，满足Mv=(M＋m)v

　　　D．小车和摆球的速度都变为v₁，木块的速度变为v₂，满足(M＋m₀)v=(M＋m₀)v₁＋mv₂

5．如图为A、B两物体相互作用前后的v-t图线，则由图线可以判断

　　　A．A、B的质量之比为3：2

B．A、B作用前后动量守恒

C．A、B作用前后动量不守恒

　　　D．A、B作用前后，总动能不变

6．A、B两球在光滑的水平面上沿一直线向同一方向运动，A球的动量是5 kg·m/s，B球的动量是7 kg·m/s，当A球追上B球发生碰撞，则碰撞后A、B两球的动量可能值是（　　）

　　　A．P_A=6 kg·m/s，P_B=6 kg·m/s

　　　B．P_A=3 kg·m/s，P_B=9 kg·m/s

　　　C．P_A=－2kg·m/s， P_B=14 kg·m/s

　　　D．P_A= －5kg·m/s， P_B=15 kg·m/s

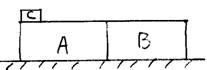
7．物体A、B用轻绳相连挂在轻弹簧下静止不动，如图所示，A的质量为m，B的质量为M，

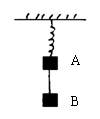　 当连接A、B的轻绳断开后，物体A上升经某一位置时速度大小为v，这时B的速度大小为u，在这段时间里，弹簧的弹力对物体A的冲量为　　　　　　　　　　　　　　　　　（　　）

　　　A．mv　　　　　　　　　　 B．mv－Mu

　　　C．mv+Mu　　　　 D．mv+mu

8．如图所示，一个质量为m的物体，在水平外力F的作用下，

　 沿水平地面匀速滑行，速度的大小为v₀。当运动到M点时撤去

　 外力F，物体由M点继续向前滑行到N点的过程中，以下说法

　 正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　A．v₀越大，摩擦力做功越多，摩擦力对物体的冲量越大

　　　B．v₀越大，摩擦力对物体的冲量越小，摩擦力做功不变

　　　C．v₀越大，摩擦力对物体的冲量越大，摩擦力做功越少

　　　D．v₀越大，摩擦力对物体的冲量越小，摩擦力做功越多

9．质量相等的五个物体在光滑的水平面上，间隔一定的距离排成一直线，如图所示，具有初动能为E₀的物块1向其他4个静止物块运动，依次发生碰撞，每次碰后不在分开，最后5个物体粘成一个整体，这个整体的动能是　　　　　 （　　）

　　　A．E₀　　　　　　　　　　  B．

C．　　  　　　　 D．

10．静止在湖面上的小船上有两个人分别向相反的方向水平地抛出质量相同的小球，甲球先向左抛出，乙球后向右抛出，抛出时两球相对于岸的速率相同，则下列说法正确的是（　　）

　　　A．两球抛出后，船向左以一定速度运动

　　　B．两球抛出后，船向右以一定速度运动

　　　C．两球抛出后，船的速度为零

　　　D．抛出时人给甲球的冲量比人给乙球的冲量大

第Ⅱ卷（非选择题 共110分）

二、本题共三小题。把答案填在题中的横线上或按题目要求作图

11．在以下实验操作中，哪几步有缺陷，并纠正之（正确的写“无”，有缺陷的写出纠正的办法）如图所示.

　　(1)用天平测出两个金属球的质量，并列表进行记录________.

　　(2)将斜槽固定在实验桌上.　

(3)将被碰小球放在小支柱上，看是否放稳____________.

(4)在地上铺一张白纸，记下重锤在纸上的垂直投影位置.（即碰撞时入射球球心的位置）

________________.

(5)让质量较小的球由静止开始从斜槽上某一高度处自由滚下，重复作10次.用圆规把小球落在地面纸上的痕迹圈在尽可能小的圆内，找出这个圆的圆心作为入射球落地点的平均位置____________.

　　(6)被碰小球放在小支柱上，让入射小球从任意高处自由滚下，使两球发生碰撞，

　　  重复作10次，用圆规画圆，确定入射球和被碰球落地点的平均位置____________.

(7)用螺旋测微器测出两小球直径，确定被碰小球碰前重心、在地面白纸上的垂直投影

　____________.

(8)用刻度尺量出各落地点平均位置到两球心垂直投影点的距离，作为两球碰撞前后的速

　度并记录，____________.

　　(9)进行计算、验证两球撞前后动量是否守恒____________.

　　(10) 为了减小误差，下面正确的选择是：

　　(A)m_入＜m_被，r_入＜r_被 ；

　　(B) m_入=m_被，r_入=r_被 ；

　　(C)降低碰撞实验器的高度；

　　(D) m_入＞m_被，r_入=r_被 .

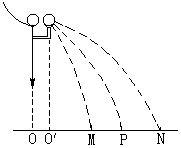
12．某次实验中在纸上记录的痕迹如图所示.测得OO^′=1.00厘米，O^′a=1.80厘米， ab=5.72厘米，bc=3.50厘米，入射球质量为100克，被碰小球质量是50克，两球直径都是1.00厘米，则入射球碰前落地点是纸上的____________点，水平射程是________厘米；被碰小球的水平射程是________厘米，碰撞前后总动量的百分误差是________ %.

13．如果P、M、N三点不在一条直线上，且偏离很大，说明实验中存在什么问题？应该如何校正？

　　　　分析解答：

　　　　

三、本题共7小题，90分。解答应写出必要的文字说明、方程式和重要的演算步骤。只写出最后答案的不能得分。有数值计算的题答案中必须明确写出数值和单位。

14．（10分）如图7-43所示，在光滑水平面上有两个并排放置的木块A和B，已知m_A=500g, m_B=300g,　一质量为80g的小铜块C以25m/s的水平初速开始在A表面滑动，由于C与A、B间有摩擦，铜块C最后停在B上，B和C一起以2.5m/s的速度共同前进，求①木块A的最后速度v'_A ②C在离开A时的速度v'_C.

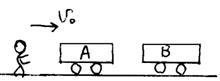
15．（12分）如图7-45所示，质量为m的人和质量均为M的两辆小车A、B处在一直线上，人以速度v_o跳上小车A，为了避免A、B相撞，人随即由A车跳上B车，问人至少要以多大的速度从A车跳向B车才能避免相撞？　　　

16．（12分）静止在太空中的飞行器上有一种装置，能向外发射一种粒子流，从而对飞行器产生反冲力，使其获得加速度.已知飞行器的质量为M，发射出的每个粒子的质量为m，速度为v，且每秒发射N个粒子，不计发射粒子后飞行器质量的变化，则射出粒子后飞行器开始运动的加速度多大？

17．（12分）一个连同装备总质量为M=100kg的宇航员，在距离飞船S=45m处与飞船处于相对静止状态，宇航员背着装有质量为m₀=0.5kg的氧气的贮气筒，贮气筒上有一个可以使氧气以v=50m/s的速度喷出的喷嘴，宇航员必须向着返回飞船的相反方向放出氧气，才能回到飞船，同时又必须保留一部分氧气供途中呼吸用，宇航员的耗氧率为Q=2.5×10^-4kg/s，则瞬时喷出多少氧气，宇航员才能安全返回飞船？

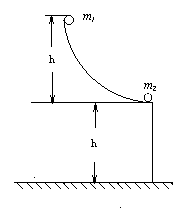18．（14分）如图所示, 在高为h的光滑平台上放一个质量为m的小球, 另一个质量为 m的球沿光滑弧形轨道从距平台高为h处由静止开始下滑, 滑至平台上与球m发生正碰, 若m= m, 求小球m最终落点距平台边缘水平距离的取值范围.

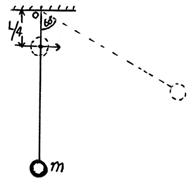
19．（15分）如图所示，长为L的轻绳一端系于固定点O，另一端系一质量为m的小球，将小球从O点正下方L/4处，以水平初速度向右抛出，经一定时间绳被拉直，以后小球将以O为支点在竖直平面内摆动。已知绳刚被拉直时，绳与竖直方向成60°角。求：

　 （1）小球水平抛出的初速度v₀；

　 （2）在绳被拉紧的瞬间，支点O受到的冲量。

20．（15分）如图所示，在光滑的水平面上，有一质量为m₁ =20千克的小车，通过几乎不可伸长的轻绳与质量m₂ =25千克的足够长的拖车连接。质量为m₃ =15千克的物体在拖车的长平板上，与平板间的摩擦系数m=0.2，开始时，物体和拖车静止，绳未拉紧，小车以3米/秒的速度向前运动。求：(a)三者以同一速度前进时速度大小。(b)到三者速度相同时，物体在平板车上移动距离。

　　　　　　　　　　　 

参考答案

题 号	1	2	3	4	5	6	7	8	9	10
序 号	AB	CD	B	BC	AB	BC	C	B	D	CD

11．(1)无　(2)斜槽末端的切线保持水平　(3)两球质心应在同一高度，保证碰撞前后瞬间速度水平　(4)白纸上铺有复写纸　(5)让质量较大的球做入射球，保证碰后两球速度方向相同　 (6)入射球每次都应从同一高度由静止开始滚下(7)无(8)无(9)无　(10)D

12．b ：8.52，　2.8 ，11.02，2.46

13．P、M、N三点不在一条直线上，说明两小球碰撞前后运动方向不在同一直线上，发生斜碰而非正碰，应左右调整小支柱的位置，使被碰小球与入射小球球心的连线与入射小球初速方向一致.

14．m_cv₀=m_Av_A’+(m_c+m_B)V　　　　 v_A’=2.1m/s--------------------------3分

C离开A时，B的速度为2.1m/s-----------------------3分

M_Cv_c'+m_B v_A’=(m_c+m_B) V　　　　 v_c'=4m/s----------------------4分

15．人跳上A车mv₀=(M_A+m)V_车-------------------------3分

人跳离A车时的速度为V₁，A车的速度为V₂，人落在B车上B车的速度为V₃

(M_A+m)V_车=m V₁+ M_A V₂-　　　------------------------3分

m V₁=(M_B+m)V₃

V₃≥V₂　　　　　　　　 -------------------------3分

解得V₁≥　　 ------------------------3分

16．设发射时间△t，发射的粒子流的质量为mN△t，-----------------------3分

动量为mNv△t，-----------------------3分

由动量守衡定律得：MV―mNv△t=0, -----------------------3分

 a=V/△t= mNv/M-----------------------3分

17．0.05kg≤m≤0.45kg：

设喷出m kg氧气能安全返回，则

由动量守衡定律得：(M―m)V+m(―v+V)=0, --------------------6分

t=S/V ， m₀=Qt+m,　--------------------3分

代入数据解得m=0.05Kg或0.45Kg---------------------3分

18．（1）正碰无动能损失，m₁和m₂碰前后速度交换--------------------3分

　　　　速度为V=　　t=

最大的位移为S₁= =2h--------------------5分

（2）若动能损失最大，两物体一起运动的速度为

V=　　　　　　　　 t=

最小的位移为S₂　=  =h　　---- ---------------5分

综合h≤S≤2h ---------------2分

19．小球被抛出后到绳拉紧前做平抛运动，绳拉紧时，小球下落高度为

h=Lcos60°－L/4=L/4

平抛运动时间= ---- ---------------5分

则小球抛出速度v₀=Lsin60°/t=

绳拉紧前瞬间，小球竖直分速度

v_y=gt=　　　　　  ---- ---------------3分

此时小球速度与竖直方向夹角为

tgα=v₀/v_y=　　  α=60°---- ---------------3分

则小球速度恰沿绳方向向外，绳拉紧时，使小球速度减为0，则绳对小球的冲量

I＝0－mv=－m=－m　　　 ---- ---------------4分

则绳对支点为的冲量大小为m，方向沿绳向外。

注意绳拉紧瞬间重力＜＜绳拉力，故忽略了重力对小球的冲量。

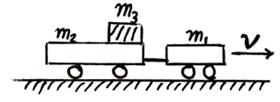
20．系统动量守恒

m₁V=（m₁+m₂+m₃）V_共

V_共=1m/s -　　　　　　  --- ---------------5分

m₁V=（m₁+m₂+）V₁  --- ---------------3分

S--- ---------------5分

解得到S=m　　　　　　　  -------------2分