模拟试卷33
一、填空题:
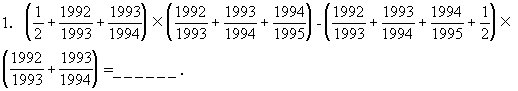
2.甲、乙两人骑车同时分别从A、B两地相对出发,甲每小时行16千米,乙每小时行14千米,两人在距中点2千米处相遇,则A、B两地的距离是______千米.
3.有五个数,每取两个相加,得到10个和,再把这十个和相加,得到的和是2064,原来五个数的和是______.
4.将1至1996这1996个自然数依次写下来,得一多位数12…,则这一多位数除以9的余数是______.
5.如图,共有长方形______个.
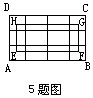
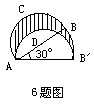
6.如图是半径为6厘米的半圆,让这个半圆绕A点按顺时针方向旋转30°,此时B点移动到B′点,则阴影部分的面积是______平方厘米.
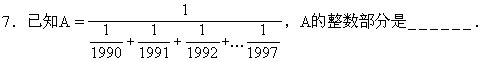
8.有一批零件由老张和小王两人合作完成,原计划老张比小王多做30个,结果小王实际做的比计划做的少20个.他做的总数比老张实际做的总数
![]()
9.有四个数,每次选取其中三个数,算出它们的平均数,再加上另外的一个数,用这样的方法计算了四次,分别得到以下四个数:22、25、34、39,那么原来的四个数中最大的一个数是______.
10.在一次国际象棋的比赛中,每两个人都要赛一场,胜者得2分,平局两人各得1分,负者得0分.现有五位同学统计了全部选手的总分,分别是551,552,553,554,555,但只有一个统计是正确的,则共有______选手参赛.
二、解答题:
1.一件工程,甲单独做16天完成,乙单独做12天完成,若甲先做若干天后,由乙接着单独做余下的工程,完成全部的工程共用了14天,问甲先做了多少天?
2.一个数,除50余2,除65余5,除91余7,求这个数是多少?
3.将200拆成两个自然数之和,其中一个是17的倍数,另一个是23的倍数,那么这两个自然数的积是多少?
4.在1,2,3,4,…,100这100个自然数中任取两个不同的数,使得取出的两数之和是6的倍数,则有多少种不同的取法?
模拟试卷33
一、填空题:
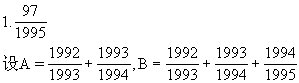
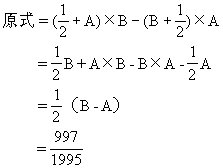
2.60
甲、乙两人相遇的时间:
2×2÷(16-14)=2(小时)
A、B两地距离:
(16+14)×2=60(千米)
3.516
设这五个数为a、b、c、d、e,每两个数相加,得到10个和,这10个和相加为:
(a+b)+(a+c)+(a+d)+(a+e)+(b+c)+(b+d)+(b+e)+(c+d)+(c+e)+(d+e)=4(a+b+c+d+e)=2064
所以a+b+c+d+e=516.
4.1
一个自然数除以9的余数等于这个自然数的各个数位上的数字之和除以9的余数.将0至1999这2000个数分成如下1000组:
(0,1999),(1,1998),(2,1997),…,(998,1001),(999,1000)以上每组两数之和都是1999,且两数相加没有进位,这样1至1999这1999个
自然数的所有数字之和是:(1+9+9+9)×1000=28000
而1997、1998、1999这3个自然数所有数字之和是:
1×3+9×6+7+8+9=81
所以1至1996这1996个自然数所有数字之和为:
28000-81=27919
(2+7+9+1+9)÷9=3…1
故多位数…1996除以9的余数是1
5.133
长方形ABCD与长方形EFGH各有长方形均为:
(1+2+3+4)×(1+2+3)=60(个)
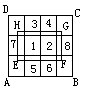
其中中间含有数字1或2的3个长方形被重复计算了,应从中去掉.
再计算特殊情况的,数字3或4所在长方形共3个,它们又与长方形EFGH共同组成了3个长方形,因此含有数字3或4的长方形个数是6个;同理含有数字5或6的长方形个数也是6个;类似得到含有7或8的长方形个数共有2×2=4个.所以图形中共有长方形的个数是:
(1+2+3+4)×(1+2+3)×2-3+6×2+2×2=133(个)
6.9.42
阴影的面积等于半圆ACB的面积加上扇形ABB'的面积减去半圆ADB'的面积,而半圆ACB与半圆ADB'的面积相等,所以阴影部分的面积就是扇形ABB'的面积,它的面积是:
![]()
7.249
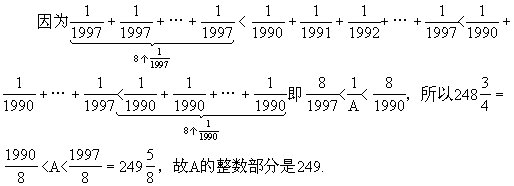
8.266
原计划老张比小王多做30个,而小王实际比计划少做20个,这样老张实际又要比计划多做20个,实际上老张比小王要多做30+20×2个,如果设老张实际做的总数是1,则老张实际做的个数:
![]()
小王实际做的个数是:
![]()
这批零件共168+98=266(个).
9.28.5
设原来的四个数是a、b、c、d,则
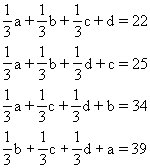
由这四个式子可以看出22+25+34+39之和恰好是a、b、c、d四个数之和的2倍,所以
a+b+c+d=(22+25+34+39)÷2=60
这四个数分别是
(22×3-60)÷2=3
(25×3-60)÷2=7.5
(34×3-60)÷2=21
(39×3-60)÷2=28.5
所以这四个数中的最大数为28.5.
10.24
因为每场比赛不论胜、负还是平局,两人得分之和是2分,所以无论有多少名选手,选手的总分应是偶数,即只有552、554中的一个是正确的.
设有n名选手参赛,则共比赛n(n-1)÷2场,选手总分:2×n(n-1)÷2=n(n-1)(分),即要求选手的总分能写成两个连续自然数之积.
由于552=2×2×2×3×23=24×23,而554=2×277.所以共有24名选手参赛.
二、解答题:
1.甲先做了8天.
设甲做了x天,则
![]()
x=8(天)
所以甲先做了8天.
2.这个数是12.
设这个数为a,则50=aq+2,aq=50-2=48,说明a48,同理a(65-5),a(91-7),则a是48、60、84的公约数,因为(48,60,84)=12,因为a>7,所以这个数只能是12.
3.所求两个自然数的积是9775.
200以内是23的倍数的数是:23,46,69,92,115,138,161,184共有八个.用200依次减去这八个数得177,154,131,108,85,62,39,16,其中只有85是17的倍数.所以200=115+85,
4.有817种不同的取法.
将这100个数分成六类,一类是被6除余1,有17个;二是被6除余2,有17个;三是被6除余3,有17个,四是被6除余4,有17个,五是被6除余5,有16个,六是被6整除,有16个.被6除余1与被6除余5的两数之和能被6整
除,共有17×16种不同的取法;同样被6除余2与被6除余4的两数之和能被6整除,共有17×17种不同的取法;再有被6除余3的数,它们中任意两数之和能被6整除,共有17×16÷2种不同的取法;同理被6整除的数,它们中任意两个数之和也能被6整除,共有16×15÷2种不同的取法.所以这100个数任取两个不同的数,使得其和是6的倍数的不同取法共有:
17×16+17×17+7×16÷2+16×15÷2=817(种).