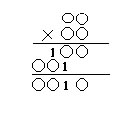小学数学奥林匹克试（决赛）

1994小学数学奥林匹克试题

决赛（民族）卷

1．计算： =_________ 。

4．5个空瓶可以换1瓶汽水，某班同学喝了161瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买汽水_________ 瓶。

5．某个自然数被247除余63，被248除也余63，那么这个自然数被26除余数是________。

6．22名家长（爸爸或妈妈，他们都不是老师）和老师陪同一些小学生参加某次数学竞赛。已知家长比老师多，妈妈比爸爸多，女老师比妈妈多2人，至少有1名男老师，那么在这22人中，爸爸有_________ 人。

7．下面有三组数：（1） （2）0.7，1.55； （3） 。从每组数中取出一个数，把取出的三个数相乘，那么所有不同取法的三个数乘积的和是_______。

8．甲、乙两管同时打开，10分钟能注满水池。现在打开甲管，9分钟后再打开乙管，4分钟就注满了水池。已知甲管比乙管每分钟多注入0.28立方米的水，那么这个水池的容积是_________ 立方米。

9．某次数学竞赛原定一等奖10人，二等奖20人，现在将一等奖中最后4人调整为二等奖，这样得二等奖的学生的平均分提高了1分，得一等奖的学生的平均分提高了3分，那么原来一等奖平均分比二等奖平均分多_________ 分。

10．有1×1×2、1×1×3、1×2×2三种木块拼成3×3×3的正方体。现有足够多的1×2×2木块，还有14块1×1×3的木块，要拼成10个3×3×3的正方体，最少需要1×1×2的木块_________ 块。

11．甲、乙、丙三人现在岁数的和是113岁。当甲的岁数是乙的岁数的一半时，丙是38岁，当乙的岁数是丙的岁数的一半时，甲17岁，那么乙现在是_________ 岁。

12．小轿车的速度比面包车的速度每小时快6千米。小轿车和面包车同时从学校开出，沿着同一路线行驶，小轿车比面包车早10分钟到达城门，当面包车到达城门时，小轿车已离城门9千米，那么学校到城门的距离是_________ 千米。

决赛试卷

1．计算： =_________ 。

3． 5个空瓶可以换1瓶汽水，某班同学喝了161瓶汽水，其中有一些是用喝剩下来的空瓶换的，那么他们至少要买汽水_________ 瓶。

4． 22名家长（爸爸或妈妈，他们都不是老师）和老师陪同一些小学生参加某次数学竞赛。已知家长比老师多，妈妈比爸爸多，女老师比妈妈多2人，至少有1名男老师，那么在这22人中，爸爸有_________ 人。

5． 盈利百分数= 。某电子产品去年按定价的80%出售，能获得20%的盈利，由于今年买入价降低，按同样定价的75%出售，却能获得25%的盈利，那么_________ 。

8． 有1×1×2、1×1×3、1×2×2三种木块拼成3×3×3的正方体。现有足够多的1×2×2木块，还有14块1×1×3的木块，要拼成10个3×3×3的正方体，最少需要1×1×2的木块_________ 块。

9． 某次数学竞赛原定一等奖10人，二等奖20人，现在将一等奖中最后4人调整为二等奖，这样得二等奖的学生的平均分提高了1分，得一等奖的学生的平均分提高了3分，那么原来一等奖平均分比二等奖平均分多_________ 分。

10．画展9点开门，但早有人来排队等候入场。从第一个观众来到时起，每分钟来的观众人数一样多，如果开3个入场口，9点9分就不再有人排队，如果开5个入场口，9点5分就没有人排队，那么第一个观众到达的时间是8点_________ 分。

11．三个自然数，其中每一个数都不能被另外两个数整除，而其中任意两个数的乘积却能被第三个数整除，那么这样的三个自然数的和最小值是_________ 。