第七届日本数学奥林匹克竞赛试题
问题1 两个整数相加时,得到的数是一个两位数,且两个数字相同;相乘时,得到的数是一个三位数,且三个数字相同。请写出所有满足上述条件的两个整数。(12分)
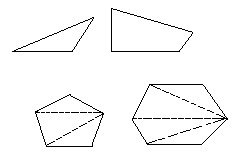
问题2 把26个玻璃球分装在a、b、c、d、e五个袋子里,每个袋里的球数不同且都装了1个以上。用一台天平称重量,当称到装有11个玻璃球的袋子时,超重警铃就会响。看下图:
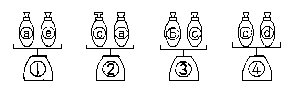
当①、③、④的状态时,警铃就响;②的状态时,警铃不响。
请按从小到大的顺序写出装入5个袋中玻璃球的数量的组合(例如: 1、3、5、7、10),并写出所有的组合。解答栏中有6组空,但不一定全部使用。(14分)
(注:不用考虑袋子的重量)
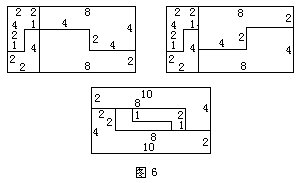
问题 3把6cm×10cm的长方形沿点线分割成4个图形,请按下面两个要求分割。
①分割后的4个图形,面积可大可小,但它们应该互为相似形。
②分割后的4个图形,可以有面积相等的,但不能都是面积相等的图形。
请回答出4种分割方法,并分别在解答栏中用实线画出。(翻转后如果同另一种分割重叠的话,将看做是同一种分割方法。)(20分)
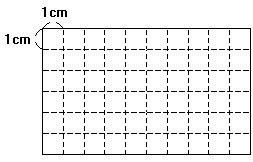
问题4 右图三角形ABC是等腰三角形。AB=AC,BAC=120°。三角形ADE是正三角形,点D在BC边上,BD∶DC=2∶3。当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?(14分)
问题5 有一只表分不清长针和短针了,多数情况下可根据两针所指的位置判断出正确的时间。但有时也会出现两种情况,使你判断不出正确的时间。请问从中午12点到夜里12点这段时间会遇到多少次判断不出的情况?(12分)(注:不包括中午12点和夜里12点)
问题6 把一个多边形沿着几条直线剪开,分割成若干个多边形。分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍。请问:①原来的多边形是几边形?②把原来的多边形分割成了多少个多边形?(14分)
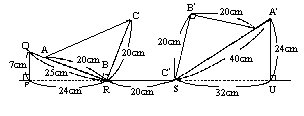
问题7 把△ABC滚到△A′B′C′的位置。求△ABC滚动过的面积。(14分)(注:圆周率取3.14)
分析与解
问题1 两个整数相加时,得到的数是一个两位数,且两个数字相同;相乘时,得到的数是一个三位数,且三个数字相同,请写出所有满足上述条件的两个整数。
分析与解 两位数中,数字相同的两位数有11、22、33、44、55、66、77、88、99共九个,它们中的每个数都可以表示成两个整数相加的形式,例如33=1+32=2+31=3+30=……=16+17,共有16种形式,如果把每个数都这样分解,再相乘,看哪两个数的乘积是三个数字相同的三位数,显然太繁琐了。可以从乘积入手,因为三个数字相同的三位数有111、222、333、444、555、666、777、888、999,每个数都是111的倍数,而111=37×3,因此把这九个数表示成一个两位数与一个一位数或两个两位数相乘时,必有一个因数是37或37的倍数,但只能是37的2倍(想想为什么?)
把九个三位数分解:
111=37×3 222=37×6=74×3
333=37×9 444=37×12=74×6
555=37×15 666=37×18=74×9
777=37×21 888=37×24=74×12
999=37×27
把两个因数相加,只有(74+3=)77和(37+18=)55的两位数字相同。所以满足见意的答案是74和3,37和18。
问题2 把26个玻璃球分装在a、b、c、d、e五个袋子里,每个袋子里的球数不同且都装了1个以上。用一台天平称重量,当称到装有11个玻璃球的袋子时,超重警铃就会响。看下图。
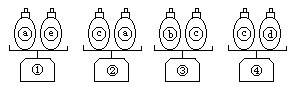
当①、③、④的状态时,警铃就响;②的状态时,警铃不响。
请按从小到大的顺序写出装入5个袋中玻璃球的数量的组合(例如:1、3、5、7、10),并写出所有的组合。
分析与解 根据题意,a、b、c、d、e袋中装的玻璃球的数量各不相同。a、b、c、d、e五个袋子里共装有26个玻璃球,这26个玻璃球的重量应是相同的,所以五个袋子的重量各不相同。用一台天平称重,当称到装有11个玻璃球的袋子时,超重警铃就会响,这一条件,应理解为天平称得的玻璃球个数是11或多于11个时,超重警铃就会响。从给出的条件可知:
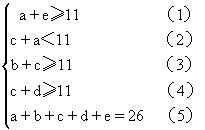
比较(2)、(3)、(4)式可知,a<b,a<d。
由(1)+(3),(1)+(4),(5)式可得:
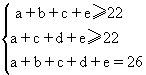
由上面的三个式子可知,b、d两袋中球的数量是4或3或2或1个,但由于a<b,a<d,所以a袋中球的数量是2或1个,b、d两袋中的球只能是4或3或2个。进一步由(2)、(3)、(4)式可知,c袋中球的数量只能是8或9个。
由此可列举出符合题意的数组,它们是:
(1、2、3、9、11)(1、2、4、9、10)
(1、3、4、8、10)(2、3、4、8、9)
问题3 把6cm×10cn的长方形沿点线分割成4个图形,请按下面两个要求分割。
①分割后的4个图形,面积可大可小,但它们应该互为相似形;
②分割后的4个图形,可以有面积相等的,但不能都是面积相等的图形。
请回答出4种分割方法,并分别在解答栏中用实线画出(翻转后如果同另一种分割重叠的话,将看做是同一种分割方法)。
分析与解 先来解释一下什么是相似形。把一个多边形的各边都扩大或缩小相同的倍数后与另一个多边形的每一对应边都完全重合,这样的两个多边形就是相似形。例如,所有的等边三角形都是相似的,所有的正方形都是相似的。
把大长方形沿点线分割成4部分,可以将其分成四个长方形。根据长方形长与宽的不同比值,结合题意,枚举出每一类可能分割出的长方形,看用哪一类中的4个长方形(面积不同的)能拼出6cm×10cm的长方形(为了叙述方便,下面省去单位)。
(一)1×n形(即长方形长与宽的比是1:n,n是整数)
(l)最小的长方形是1×1,与它相似的长方形有2×2,3×3,4×4,5×5,6×6。
可以分割出6×6的长方形(见图1)。
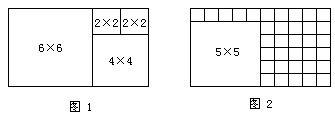
不能分割出5×5的长方形(见图2),因为不论把5 × 5的长方形放在6 × 10的长方形中的哪一位置,在这个5×5的长方形的上边(或下边)的5个小正方形,只能分割成5块1×1的长方形,这显然不合题意。
分割出的长方形中最大的不可能是4×4或更小的。因为(4 × 4)× 4= 64> 6 × 10,(4 × 4) × 3+(3 × 3)×1=57< 6 × 10。
(2)最小的长方形是1×2,与其相似的长方形有2×4,3 × 6,4 × 8,5 × 10。
不能分割出5×10的长方形(分析同(1)中 5×5)。
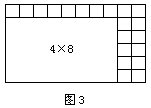
也不能分割出4×8的长方形(见图3),因为6×10-(4 × 8) ×1=32,(2 × 4)×3= 24<32。
还不能分割出3×6的长方形。不能分出4个3×6的长方形,因为(3 × 6)× 4=72> 6 × 10。不能分出3个3×6的长方形,因为6×10-(3×6)×3=6, 1×2=2< 6,2 × 4 = 8>6。不能分出2个3×6的长方形,因为60-(3×6)×2=24,(2×4)×2=16<24,也不能分出1个 3×6的长方形,因为(3×6)×l+(2×4)×3=42<60。
更不能分割出2×4或回1×2的长方形,因为(2×4) × 4=32< 6×10。
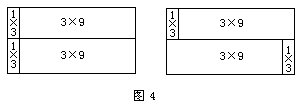
(3)最小的长方形是1×3,与其相似的长方形有2×6,3×9。
可以分割出3×9的长方形(见图4)。
不能分割出2×6的长方形,因为(2×6)×4=48< 6×10。
(4)最小的长方形是1×4,与其相似的长方形有2×8,这样的两个长方形都不能分割出来。因为(2×8)×4=64>6×10,(2×8)×3+(1×4)×1=52<6×10。
(5)最小的长方形是1×5,与其相似的长方形有2×10,这样的两个长方形都不能分割出来。因为(2 ×10)×3=6×10,(2×10)×2+(1×5)×2=50< 6×10。
(6)同样可以证明不能分割出 1×6、1×7、1×8、1×9、1×10这些长方形。
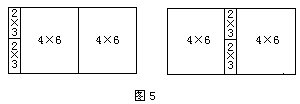
(二)对于2×n、3×n、4×n、5×n形的长方形,按照(一)的分析方法,可以找到一种符合题意的分割方法(见图5)。
也可以把6×10的长方形沿点线分割成其他多边形(见图6)。
问题4 下图三角形ABC是等腰三角形。AB=AC,∠BAC=120°。
三角形ADE是正三角形,点D在BC边上,BD∶DC=2∶3。
当三角形ABC的面积是50cm2时,三角形ADE的面积是多少?
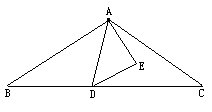
分析与解 以点A为中心,由三个三角形ABC可拼成右图:
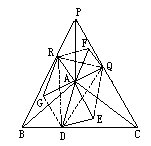
连结QE、RF、GD,则DEQFRG是一个正六边形。连结RD、DQ、RQ,显然RDQ是一个等边三角形,并且它的面积是正六边形面积的一半。
S△PBC=S△ABC×3=150cm2,
![]()
S△RDQ=S△PBC-S△DQC×3=42cm2,
S△ADE=S△正六边形÷6=2×S△RDQ÷6=14cm2。
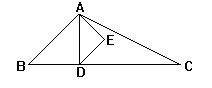
问题5 有一只表分不清长针和短针了,多数情况下可根据两针所指的位置判断出正确的时间。但有时也会出现两种情况,使你判断不出正确的时间。请问从中午12点到夜里12点这段时间会遇到多少次判断不出的情况?(注:不包括中午12点和夜里12点)
分析与解 当表在某点某分时,经过一段时间后,如果时针恰好走到原来分针的位置,而分针恰好走到原来时针的位置,即两针位置互换,由于分针、时针分辨不清,所以凡能发生两针位置互换的两个时刻都不能正确的判断当时的时间(如下图)。
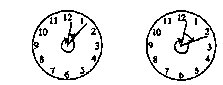
两针位置互换,当时针、分针共走60格时,由于时针走1格,分针走![]()
午12点多至1点多,1点多至2点多,2点多至3点多……夜里10点多至11点多,共11次。
同样可以算出两针位置互换时针、分针共走120、180、240、300、360、420、480、540、600、660格时,可以出现两针位置互换的次数分别是10、9、8、7、6、5、4、3、2、1次,所以分辨不出正确时间的次数共有(11+10+9+8+7+6+5+4+3+2+1)×2=132次。
注:题目只要求我们算出分辨不清时间的次数,所以没有必要算出具体的时间。
问题6 把一个多边形沿着几条直线剪开,分割成若干个多边形。分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍。请问:①原来的多边形是几边形?②把原来的多边形分割成了多少个多边形?
分析与解 先来观察下面这组图形:
容易看出,n边形有n个顶点,n边形是由(n-2)个三角形组成的。因此,知道了一个多边形的边数或顶点数(n),就可以求出它的内角和(n-2)×180°,知道了一个多边形由多少个三角形(m)组成的,就可以求出它的边数或顶点数(m+2)。
设原多边形是由a个三角形组成的,分割后的多边形共由b个三角形组成,a和b都是整数,根据题意有:
1.3×a×180°=b×180°,于是有1.3a=b。
由于b是整数,所以1.3a也是整数,a必是10的倍数,于是1.3a是13的倍数,b也是13的倍数。
(一)设a=10,则b=13,进而可知原多边形有12个顶点(12条边),而分割后的多边形有15个顶点(15条边)。
由于连结一个多边形的两顶点时,将一个多边形分成两个多边形后,顶点的数目不变,而分出的两个多边形比原来增多2条边。连结多边形的一个顶点与一边上一点时,顶点数目增多1个,而分出的两个多边形比原来增多3条边。连接两边上一点时,顶点数目增多2个,而边数比原来增多4条。要增多(15-12=)3个顶点,增多13条边,有两种连线方法。(见下图)

显然原多边形是12边形,两种连结方法都将12边形分成了6个多边形。
(二)如果a=20,则b=26,原多边形有22个顶点,而分割后的多边形有28个顶点,增多了(28-22=)6个顶点,不论怎样连结都不能使分割后的多边形边数总和比原来的多边形增多13条边。因此原多边形不是22边形。
如果a更大,则分割后增加的顶点个数更多,不论怎样连结都不符合题目要求。因此原多边形只能是12边形。
问题7 把△ABC滚到△A′B′C′的位置。求△ABC滚动过的面积(注:圆周率取3.14)。
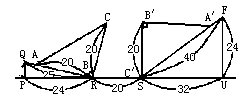
分析与解 画出△ABC滚动到△A′B′C′的位置时滚动的轨迹图,如下:
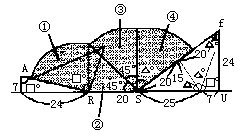
△ABC滚动过的面积可分成三部分:第一部分是以R为圆心,三角形的直角边为半径的扇形①;第二部分即三角形ABC②;第三部分是以S为圆心,三角形的斜边为半径的扇形(③+④)。
分别计算图中①、②、③、④部分的面积:

由勾股定理可知:AC×AC=AB×AB+BC×BC=800。
分割三角形svf(见上图),易知分出的三个三角形都是直角三角形,△°×2+□°=180°。
由于
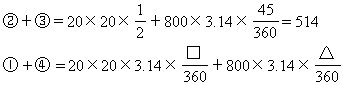
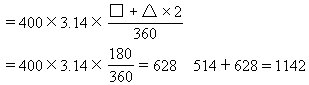
△ABC滚动过的面积是1142cm2。