| 1.计算: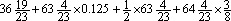 =________。 =________。
2.一个千位数字是1的四位数,当它分别被四个不同的质数相除时,余数都是1,满足这些条件的最大的偶数是 ____。
3.有两个三位数,它们的和是999,如把较大数放在较小数的左边,点一个小数点在两数之间所成的数,正好等于把较小数放在较大数的左边,点一个小数点在两数之间所成的数的6倍,那么这两个数的差(大减小)是 ________。
4.一千个体积为1立方厘米的小立方体合在一起成为一个边长为10厘米的大立方体,表面涂油漆后再分开为原来的小立方体,这些小立方体中至少有一面被油漆涂过的数目是_______。
5.某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人至多参加两科,那么参加两科的最多有_______人。
6.甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米处;如果两人各自的速度不变,要使甲、乙两人同时到达终点,甲的起跑线应比原来的起跑线后移_______米。
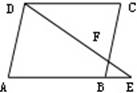
7.一水池有一根进水管不断地进水,另有若干根相同的抽水管。若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可将池中的水抽干。若用16根抽水管抽水,_______小时可将池中的水抽干。 | 8.如右图, P为平行四边形ABCD外一点,已知三角
形PAB与三角形PCD的面积分别为7平方厘米和3平
方厘米,那么平行四边形ABCD的面积为_______平方厘米。 | 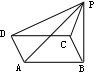
| 9.甲、乙、丙三人跑步锻炼,都从A地同时出发,分别跑到B,C,D三地,然后立即往回跑,跑回A地再分别跑到B,C,D,再立即跑回A地,这样不停地来回跑。B与A相距 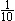 千米,C与A相距 千米,C与A相距 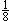 千米,D与A相距 千米,D与A相距 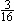 千米,甲每小时跑3.5千米,乙每小时跑4千米,丙每小时跑5千米。问:若这样来回跑,三人第一次同时回到出发点需用_______小时。 千米,甲每小时跑3.5千米,乙每小时跑4千米,丙每小时跑5千米。问:若这样来回跑,三人第一次同时回到出发点需用_______小时。
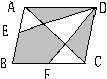
10.一个盒子里面装有标号为1到100的100张卡片,某人从盒子里随意抽卡片,如果要求取出的卡片中至少有两张标号之差为5,那么此人至少需要抽出_______张卡片。 | 11.8点10分,有甲、乙两人以相同的速度分别从相距60米的A,B两地顺时针方向
沿着长方形ABCD(见右图)的边走向D点,甲8点20分到D后,丙、丁两人立即
以相同的速度从D点出发,丙由D向A走去,8点24分与乙在E点相遇,丁由D向C
走去,8点30分在F点被乙追上,则连接三角形BEF的面积为________平方米。 | | 
| 12.今有长度分别为1厘米、2厘米、3厘米、...、9厘米长的木棍各一根(规定不许折断),从中选用若干根组成正方形,可有_______种不同方法。 |