奥数小学一年级:
内容主要有两大块:几何入门和数字研究。
(一)几何:
数学可以分为两个大类:代数和几何。代数主要是研究数,式子,方程等问题的,而几何这门学科,主要研究图形,研究现实空间中的点,线,面和体,相对代数而言,要求有更高的空间想象能力。
学习几何,要有动手的习惯。可以自己做实验,也可以通过观察发现和体会几何知识。在初中会研究平面几何,高中研究立体几何。所谓平面几何,就是指只研究一个面上的东西,例如:点,直线,三角形等。立体几何研究三维空间的立体形状,向一个箱子(长方体),一个篮球(球体),一个瓶子(柱体)等等。
1.基本单元:
![]() 用笔在纸上画一个点,可以大些,也可以小些。点在纸上只占一个位置。
用笔在纸上画一个点,可以大些,也可以小些。点在纸上只占一个位置。
![]()
![]()
![]() 线段有两个端点,有固定的长度,也可以理解为用直尺把两点连接起来。
线段有两个端点,有固定的长度,也可以理解为用直尺把两点连接起来。
![]() 射线,从一点出发,另一头延伸出去,没有尽头。
射线,从一点出发,另一头延伸出去,没有尽头。
![]()
![]() 直线,两端没有端点,可以向两端无限延伸,没有固定长度,是不可以测量出长度的。
直线,两端没有端点,可以向两端无限延伸,没有固定长度,是不可以测量出长度的。
2.线与线的位置关系:
 |
![]()
![]()
![]()

相交关系 平行关系(永远没有交点) 垂直(相交的一种)
3.角:
线与线可以组成角。两个不同的射线,出发点相同,沿不同的方向延伸,就可以构成角。
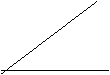 |  | 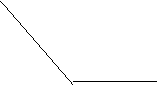 | |||
锐角 直角 钝角
锐角<直角<钝角 直角是两者相互垂直
角度范围:0~180
0<锐角<90 直角=90 90<钝角<180
4.多边行之一:
由直线可以构成若干边行,最少为三角形,其他的有四边行,五边行等等。
根据角的关系研究:
a.三角形:直角三角形,锐角三角形,钝角三角形。
一个角为直角,就是直角三角形。
三个角都是锐角(全小于90度),是锐角三角形。
一个角是钝角三角形,就是钝角三角形。
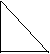 | 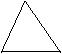 | 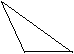 |
所有的三角形的三个角度之和为180度。
b.根据边的关系研究:
三角形:等腰三角形,等边三角形,不等边三角形。
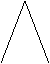
![]()
![]()
![]()
![]()
![]()
![]() 根据三条边的关系来划分它们。
根据三条边的关系来划分它们。
其中,等腰三角形要求是至少两个边相等(第三边可以相等,也可以不等),等边三角形是三个边都相等,不等边三角形是三条边中没有相等的边。
c.角与边的结合:
按照角和边,是两种完全不同的划分方法,也可以把它们结合起来研究。
如:
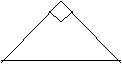 | 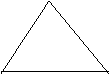 | ||
等腰直角三角形
等边三角形(锐角三角形)
而且,三个角度都是60度。
5.多边行之二:
四边行有很多的种类,我们只研究其中最特殊的几种。
长方形(矩形),正方形,梯形,平行四边形,菱形等。
它们的分类:
![]()
![]()
|
正方形
菱形
-----梯形
一组对边平行,另外的一组不平行,为梯形。
两组对边平行且相等,(两组对角相等)为平行四边形。
两组对边平行且相等,四个角都是直角,为长方形。
四条边都相等(四个角也相等),是菱形。
四条边都相等,四个角都是直角,是正方形。正方形既满足长方形的要求,又哦满足菱形的要求,所以它是非常特殊的一种四边形状。
 |  |  | |||||||
![]() 梯形
平行四边形
矩形
菱形
正方形
梯形
平行四边形
矩形
菱形
正方形
 |
6.多边行之三:圆及相关图形
 | |||||
 |  | ||||
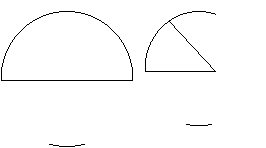
圆 半径,直径和圆心 半圆 扇行
由曲线构成的完美图形。注意:圆是以圆心为中心,以半径为长度,用圆规旋转一周围成的圆。扇行由圆弧和两个半径组成。
围绕一周的度数是360度。
练习:
1, 数一数,下图有几条线段?
![]()
2, 数一数,下图中总共有几个角?
 |
3, 下图共有多少个三角形?
![]()

![]()
4, 下图共有多少个长方形?

5, 下图共有14个正方形,你能找出来吗?
6, 下图共有多少个三角形?
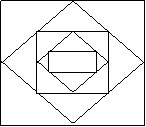
7.使用三角板和圆规画图:
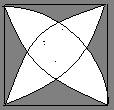

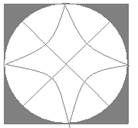
8,用三根火柴棍可以摆一个三角行,如图:
(1) 再加两个火柴棍,摆出两个三角形
(2) 再加两个火柴棍,摆出三个三角形
(3) 再加两个火柴棍,摆出五个三角形
学习完二维空间的点,线和面,我们开始学习三维的立体几何。
我们称之为:体。
长方体,立方体,圆柱,圆锥,棱柱,棱锥,球体。
关于立体几何,有很多的公式,要求有丰富的空间想象能力,可以把它和我们的现实生活联系起来。对于下面研究的图例,它们的面积和体积全部都有固定的公式,我们只要求认识这些图形,不要求记住公式。

长方体 就是每个面由长方形构成,总共有6个面,就有6个长方形。
![]()
![]()
![]()
![]()
![]()

![]()
正方体 由6个正方形构成,每条边长都一样。有12条棱。
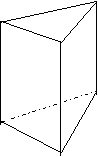 | |||
 | |||
圆柱体 两个底面是完全相同的圆。 三棱柱 上下底面是三角形
柱体与锥体:两端相同的,成对称的立方体;而锥体是一端是点,另一端是图形(圆或者多边形)。
 |  | ||||
 | |||||
 | |||||
圆锥 三棱锥(四面体) 四棱锥
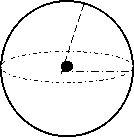
球,可以理解为是圆的立体化。最中心的地方叫做球心,到球面的距离叫做球的半径。
立体图形,要有立体的想象能力,下面,我们把立体的图形解剖开来,看看它们的平面效果。
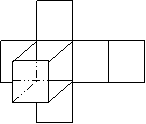 | |||
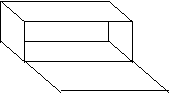 |
长方体展开图示:
圆锥展开图形 四棱锥展开图
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
你能看出来它们是什么吗?
 | |||
 | |||
![]()
![]()

你知道他展开后是什么样子的吗?
 |
观察下面的图形中阴影部分占整体的几分之几?
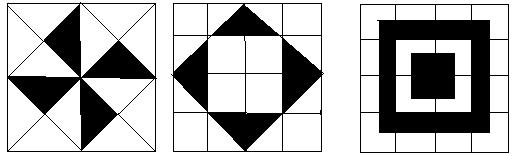
图形的等积变化和等积划分问题:
在奥数中通常会碰到一些比较怪异的图形,我们最常用的方法就是把它进行等积变化,变成可以计算的规则的图形。
等积划分就是把一个不规则的图形如何分为面积相等的两份,观察是最重要的途径。
1, 变梯形为三角形:
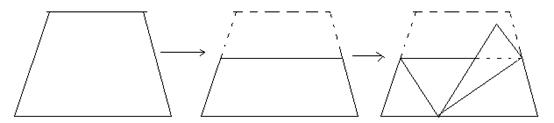
可以自己动手做一做!
2,经典问题:五个小正方形,变成一个大正方形:
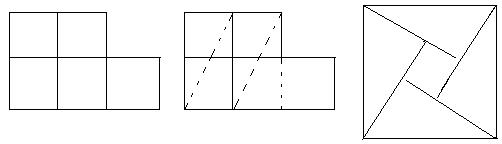
3,如何把正方形再拼成一个等腰直角三角形?
 |
把图形分成面积相等的几分,关键在找到对称点,找到使两个或者多个单独的部分有相同的形状和结构。
1,分下面图形成面积相等的两部分:
![]()
2,分下面的图两个相等的部分:
![]()
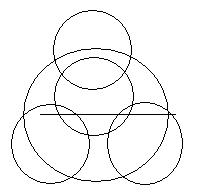
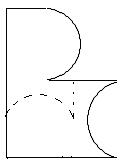
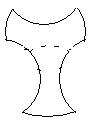
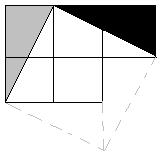
如图,如何把院子里的12棵树分成大小相等,形状相同的4个小区,每个小区有3棵树?
| 第二部分 运算技巧与数的知识 |
数字与运算系列:(一)
数字的运算求和,要善于发现他们之间的规律,找到捷径和简单的方法
1,计算: 1+3+5+7+9+11+13+15+17+19
2, 计算:10-9+8-7+6-5+4-3+2-1
3, 计算:(2+4+6+8……+100)-(1+3+5+7+…. +99)
4,时钟1点钟敲了1下,2点钟敲了2下,3点钟敲了3下,………………..照这样做下去,从1点到12点,这12个小时时钟共敲了几下?如果每半小时,时钟都敲一下,那这12小时内共敲了多少下?
5,(1)把16只小鸡分别装进5个笼子里,每个笼子都要有鸡,而且每个笼子里的鸡的只数也不能相同,如何分装?
(2)按同样的要求,把15只小鸡装进5个笼子能半的到吗?14只呢?
(分析,实验,可以从简单的问题入手,用已知的数字带入看看)
6,把100块糖分给10个小朋友,要求每人都分到单数块糖,而且每人分到糖快数都不一样,如何分?要是分99块糖给10个人呢?(常见的数字和要记得)
| 数数和计数问题:原则就是不能漏掉,也不能重复。如果可以,尽量画图示意,把重复的内容删除掉 |
7,少先队员去科技馆,从排头数起,刘平是第20个;从排尾数起,张英是第23个。已知刘平的前一个是张英。问这队少先队员共多少人?(41)
8, 一班同学做花,做红花的有38人,做黄花的有39人,没有做花的有3人。如果全班55
人,那么既做红花又做黄花的有多少人?
| 植树问题:棵数-1=间隔数 |
9,小明在马路的一边种树,每隔1米种一棵树,共种了11棵,问这段马路有多长?
10, 钟楼的钟打点报时,5点钟搭下要4秒钟,问12点时打12下要几秒钟?(注意联系
实际,分析过程,属于植树问题)
11, 小明与爸爸一同上楼。小明跑的比爸爸快,爸爸上的慢,小明上2层,爸爸上1层。
问小明上到5楼时,爸爸上到几楼?(竞赛题)
| 所谓枚举法就是用简单的数数的方法,把你知道的全部写出来,再计算它们的总和。 |
12,分别用有数字1,8,3的三张卡片,能排出多少个不同的2位数来?(自己列举例子)
13手问题:有一群人,若规定每两个人都握手一次而且只握一次手,求他们共我多少次手?假使这群人是:1,两个人,2,三个人,3 ,四个人?
(图形解决的特殊方法)
14铁路上的火车票价是根据两站距离的远近而定的,距离愈远,票价愈高。如果一段铁路上共有5个站,每两站间的距离都不相等,问这段铁路上的火车票价共有多少种?(画图法)
15(数字游戏):如下图所示,把1,2,3,4,5,6,7,8,9分为三组,填到三个小三角形的各个角上的圆圈里,使每个小三角形的三个角的圆圈里的数之和都是15。同时使大三角形三个角的圆圈里的数之和也是15。

对于前面的题,多数是已经列好算式要求计算出结果,但在这里,我们却是知道结果和要达到的目标,请你回答如何能得到这种结果。这也是数学竞赛时经常见到的题型。
要求能进行大胆的尝试,培养思维的灵活性和敏捷性,仔细观察,发现题中给出的一些关于数的规律。
1,某公园有三棵树,树的年龄分别是由1,2,3,4,5,6这6个数字中的不同的两个数字组成,而且其中一棵的树的年龄正好是其他两棵树年龄和的一半,问这三棵树的年龄个是多少?
2,见右图。有一天,钟从墙上掉下来,钟面摔成了三块。三块的形状虽然不同,但三块的数相加之和却是相等的。请问你知道他们碎成什么样子吗?每块钟面上的数的和是多少?
3,比赛题:一只老猫捉了12只老鼠,其中有一只是小白鼠。老猫自言自语说:“我要分三批吃它们。不过吃以前叫它们站好队,我从头一个开始吃,隔一个吃掉一个,也就是:我第一次吃掉站在1,3,5,7,9,11号位置的老鼠;剩下的叫它们不许动,第二次还是从头一个吃,隔一个吃一个;第三次也是照这样的方法吃。但把最后一个放了。”这话被聪明的小白鼠听见了,于是它站在了某个位置上,没有被吃掉。请问你知道它站在几号位置上了吗?
(画图找规律)
在数学中,经常研究相等关系,可有时候还研究不等关系。除了等于=之外,还有不等于<>
,>,<等关系。
一,如 1<2, 1<=2, 2=2,2>=2,3>3, 3<>2.你知道它们的意思吗?用不等关系,可以排除许多的无关信息,在高中阶段,有专门研究不等关系的内容,如列不等式解方程,不等函数等。
在我们目前接触的整数中,如1,2,3,4,100,200等,可以把数分为奇数和偶数。而不
二,对小数作这样的分类。偶数就是可以被2整除的数,所谓的整除就是用它来除以2时,没有余数,象2,4,6,8,10,…..,100,102,
……………;而奇数就是那些不能整除2的数,简单的说就是除以2后,有余数1,如:1,3,5,7,9,…………………..
三,数学中还存在这样的一类型的数,叫布尔型。就有两个结果:是或者否,T和F。(也可以理解为对或者错。)
1, 老师发了数学考卷,一班(1)组的六个同学的分数是这样的:
小王和小钱的分数一样的多;
小赵比小李的分数多,可比小王的分数少;
小乐没有小王,小赵的分数多,但比小李的分数多;
小钱的分数比小顾的又要少一些。
请问他们谁的分数最多,谁的最少?
2, 红球比白球大;蓝球比黄球大,比黑球小;黄球比白球大;黑球比红球小。请按照顺序排列它们?
3前十个自然数的和是奇数还是偶数?
4把10个球分为三组,要每组都是奇数,怎样分?
(您知道0是什么数吗?)
5有的电影院的座位号码是单号与单号相邻,双号与双号相邻。
(1) 一个人拿了三张单号的电影票,这三个号码相加之和是9,问这三个座位分别是几号?
(2) 若三张号码相加之和等于15呢,三个号码是多少?
(3) 若三张号码相加之和等于21呢,三个号码是多少?
6小华说:“我爸爸是厂长,但我不是他这个厂长的儿子”。你认为小华的说法一定错了吗?为什么?
7在等腰直角三角形中,必定有两条边相等,而且必定有一个角是直角,对吗?任意两条边的和都比第三边大,对吗?(是非题)