操作问题
84 黑板上有5和7两个数。现在规定操作:将黑板上的任意两个数相加的和写在黑板上。问:经过若干次操作后,黑板上能否出现23?
85 有一台古怪的计算器,只有两个运算键,红键把给的数乘以2,黄键把给的数的最后一个数字去掉。例如,给出234,按红键得468,按黄键得23。如果开始给的数是28,为了得到数17,那么除了按若干次黄键外,至少要按红键多少次?
86 黑板上写着8,9,10,11,12,13,14七个数,每次任意擦去两个数,再写上这两个数的和减1。例如,擦掉9和13,要写上21。经过几次后,黑板上就会只剩下一个数?这个数是几?
87 在黑板上任意写一个自然数,然后用与这个自然数互质并且大于1的最小自然数替换这个数,称为一次操作。问:最多经过多少次操作,黑板上就会出现2?
88 在黑板上写出三个自然数,然后擦去一个换成其它两数之和减1,这样继续操作下去,最后得到32,45,76。如果要求原来写的三个自然数的和尽量小,那么它们是哪三个自然数?
89 在上题中,若把最后得到的三个数改为15,35,49呢?
90 对任意两个不同的自然数,将其中较大数换成这两数之差,称为一次变换。如对18和42可作这样的连续变换:
18,42→18, 24→18,6→12, 6→6,6
直到两数相同为止。问:对1234和4321作这样的连续变换,最后得到的两个相同的数是几?
91 对任一自然数n作变换:如果n为奇数,则加上99;如果n为偶数,则除以2。现在对300连续作这种变换,在变换过程中是否可能出现100?为什么?
92 口袋里装有99张小纸片,上面分别写着1~99。从袋中任意摸出若干张小张片,然后算出这些纸片上各数的和,再将这个和的后两位数写在一张新纸片上放入袋中。经过若干次这样的操作后,袋中还剩下一张纸片,这张纸片上的数是几?
93 将40以内的质数从小到大排成一个数字串,依次完成以下五项工作叫做一次操作:
(1)将右边第一个数码移到数字串的最左边;
(2)从左到右两位一节组成若干个两位数;
(3)划去这些两位数中的合数;
(4)如果所剩的两位质数中有相同的,那么只保留左边的一个,其余的划去;
(5)所剩的两位质数,保持数码次序又组成一个新的数字串。
问:经过99次操作,所得的数字串是什么?
94 在一个圆上标出一些数,第一次先把圆周二等分,在两个分点分别标上1和2。第二次把两段半圆弧分别二等分,在分点标上相邻两分点两数的和3(见左下图)。第三次把四段弧再分别二等分,在4个分点分别标上相邻两个分点两数的和。如此下去,当第六次标完数以后,圆周上所有标出的数的总和是多少?
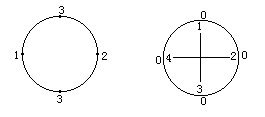
95 右上图是一个圆盘,中心轴固定在黑板上。开始时,圆盘上每个数字所对应的黑板处均写着0。然后转动圆盘,每次可以转动90°的任意整数倍,圆盘上的四个数将分别正对着黑板上写数的位置,将圆盘上的数加到黑板上对应位置的数上。问:经过若干次后,黑板上的四个数是否可能都是1999?
![]()
96 在右图的方格表中,每次给同一行或同一列的两个数加1,经过若干次后,能否使表中的四个数同时都是5的倍数?为什么?
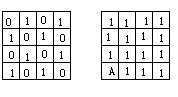
97 在左下图中,对任意相邻的上下或左右两格中的数字同时加1或减1,这算作一次操作。经过若干次操作后变为右下图。问:右下图中A格中的数字是几?
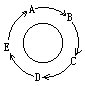
98 五个小朋友 A, B, C, D, E围坐一圈(如右图)。老师分别给A,B,C,D,E发2,4,6,8,10个球。然后,从A开始,按顺时针方向顺序做游戏:如果左邻小朋友的球的个数比自己少,则送给左邻小朋友2个球;如果左邻小朋友的球的个数比自己的多或者同样多,就不送了。如此依次做下去,到第四圈为止,他们每人手中的球的个数分别是多少?
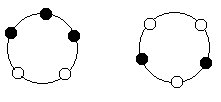
99 左下图中有 5个围棋子围成一圈。现在将同色的两子之间放入一个白子,在异色的两子之间放入一个黑子,然后将原来的5个子拿掉,剩下新放入的5个子如右下图,这算一次操作。如果继续这样的操作,那么一圈的5个子中最多时能有几个黑子?
100 六个盘子中各放有一块糖,每次从任选的两个盘子中各取一块放入另一个盘子中,这样至少要做多少次,才能把所有的糖都集中到一个盘子中?
101 将 1~ 10这 10个数随意排成一排。如果相邻两个数中,前面的大于后面的,就交换它们的位置。如此操作直到前面的数都小于后面的数为止。已知10在这列数中的第6位,那么最少要进行多少次交换?最多要进行多少次交换?
102☆下图是一个4×5的方格纸。先将其中的任意 4个方格染黑。然后按以下规则继续染色:如果某个格至少与两个黑格都有公共边,就将这个格染黑。这样操作下去,能否将整个方格纸都染成黑色?
