探索与归纳训练A卷
班级________ 姓名________ 得分________
1.(1)计算下列各题,你能发现从1起求若干奇数和的规律吗?
1+3=
1+3+5=
1+3+5+7=
1+3+5+7+9=
(2)求1+3+5+……+99=
(3)想一想,怎样计算下列各数的和。
101,103,105,……,199。
2.用花、白两种正方形的瓷砖拼成大的正方形图形,要求中间用白瓷砖,四周一圈用花瓷砖(如下图所示)。
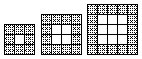
(1)填写下列表格。想一想,这些数量之间有什么关系?
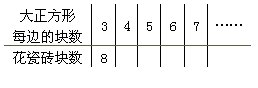
(2)如果所拼的图形中,用了100块白瓷砖,那么,花瓷砖用了多少块?
(3)如果所拼的图形中用了100块花瓷砖,那么白瓷砖用了多少块?
3.用若干相同的小等边三角形,可以拼成大的等边三角形。(如下图所示)
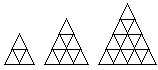
(1)填写下面表格,想一想,小三角形的个数与大三角形的层数有什么关系?

(2)如果拼成的大三角形有 30层.那么共用了多少个小三角形?
4.把一张长方形纸对折再对折,然后在折叠着的角上剪一刀,纸的中间就剪出了一个洞(如下图所示)。
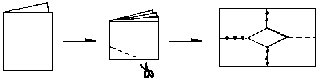
(1)填写下面表格。想一想,对折的次数与剪出洞的个数有什么关系?
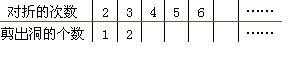
(2)如果对折了10次后,再在折叠着的角上剪一刀,那么这张纸上共剪出了多少个洞?
5.用火柴棒搭成两排大小相等的正方形(如下图所示)。
![]()
(1)填写下面表格,想一想,小正方形的个数与所用火柴棒的根数有什么关系?
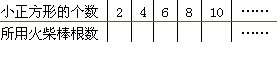
(2)如果搭12个这样的正方形,那么需要多少根火柴?
(3)用157根火柴可以搭成这样的正方形多少个?
6.第一次把一根一米长的木棒锯成相等的两段,第二次再把锯成的两段各锯成相等的两段。至少经过几次这样的操作后,每段木棒的长度小于1厘米?
7.如果在下面45个空格内分别填上这空格所在行和所在列的两个数的和。问这45个数的总和是多少?
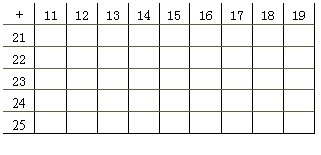
8.已知1995年元旦是星期日,2000年的元旦是星期几?
9.从长方形左下方的顶点发出一道光束,光线按45°角前进,碰到正方形的边即呈45。角折射,最后从长方形顶点射出(如下图)。

这样,光线从发出点到终点共通过6个小方格。
(1)调查光线通过的小正方形个数与长边、宽边上小正方形个数的关系。

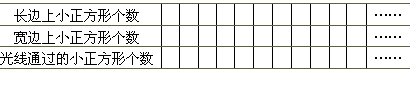
光线通过的正方形个数与长边、宽边上的正方形个数有什么关系?
(2)用你发现的规律计算下面各题。
