第一章 证明（一）
班级 姓名 学号 成绩
一、填空题（1—6小题每空1分,7—13小题每题2分,共30分）
1.等腰三角形的两底角 ,反之有两个角 的三角形是等腰三角形.
2.等腰三角形 、 、 互相重合,简称“三线合一”.
3.用反证法证明,先 的结论不成立,然后推导出
从而证明原命题的结论 ,这种证明方法称为反证法。
4.命题“中国人都是黄皮肤”的逆命题是
,它是一个 命题.
5.如图,∠C=∠D=90°,要使△ABC≌△BAD,还需
补充的条件是 或
或 。
6.到△ABC三个顶点距离相等的点是
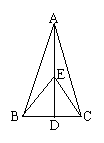到△ABC三边距离相等的点是
。
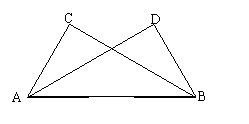
7、如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形
有 对,它们是
(用符号表示)
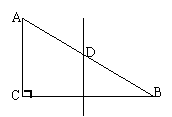8、如右图所示,在△ABC中, ∠C=90°,AB=16㎝,BC的
垂直平分线交AB于点D,则点C与点D的距离
是 ㎝。
9、三角形三内角的度数之比为∠A:∠B:∠C=1:2:3,BC=3㎝,则AB= ㎝,AC= ㎝.
10、在△ABC中，已知∠B和∠C的平分线交于点O，∠BOC=135°，则△ABC是 三角形。（填“钝角”或“等腰”或“等边”或“直角”）
11、直角三角形两边长分别是3㎝和4㎝,则第三边长 ㎝。
12、在平静的湖面上有一支红莲，高出水面1米，一阵风吹来，红莲吹到一边，花朵齐及水面，已知红莲移动的水平距离为2米，那么红莲生长处的水深是 米。
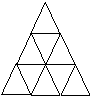
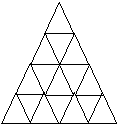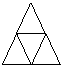
13、现有边长为1的等边三角形卡片若干张，使用这些三角形卡片拼出边长分别是2，3，4…的等边三角形，如下图所示，根据图形规律推断，每个等边三角形所用卡片总数S与边长n之间的关系式为
。
 | |||
 | |||
……
二、选择题。（每小题3分，共24分）
14.下列不属于等边三角形的判定方法的是 （ ）
A. 三边相等的三角形是等边三角形
B. 三内角相等的三角形是等边三角形
C.有一个角等于60°的等腰三角形是等边三角形
D.有两个外角相等的等腰三角形是等边三角形
15、下列条件中不能判定两个直角三角形全等的是 （ ）
A.斜边和一直角边对应相等 B.有两条边对应相等
C. 有两个锐角对应相等 D.有一个锐角和一条边对应相等
16、下列命题中，其逆命题为真命题的是 （ ）
A. 直角都相等 B.面积相等的两个三角形全等
C. 等边三角形是锐角三角形 D.若a=b,则a2=b2.
17、以下作图中，不能用尺规完成的是 （ ）
A.将一个已知角两等分 B. 将一个已知角三等分
C.作一个角等于已知角 D.作已知线段的垂直平分线
18、等腰三角形两边长分别是2㎝和3㎝，则周长是 （ ）
A.7㎝ B.8㎝ C.7㎝或8㎝ D.条件不足，无法求出
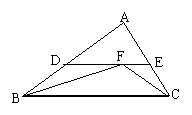
19、如图，在△ABC中，已知∠ABC和∠ACB的平分线
交于点F,过F作DE∥BC,交AB于点D,交AC于点E,
如果BD＋CE=9,那么DE等于 （ ）
A.9 B.8 C.7 D.6
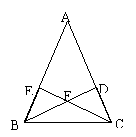20、如图，在△ABC中,AB=AC, BD、CE分别是∠ABC和∠ACB的
平分线，且相交于点F，则下列说法中错误的是（ ）
A.BF=CF B.CE=BD
C.点F到∠BAC两边的距离相等
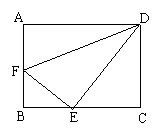D.点F到点A、B、C三点的距离相等
21、如右图所示，折叠矩形ABCD，使点A落在BC边
的点E处，DF为折痕，已知AB=8㎝,BC=10㎝,
则BE的长等于 （ ）
A.4㎝ B.5㎝ C.6㎝ D.7㎝
三、解答题。（22—27小题为必做题，28—30小题为选做题）
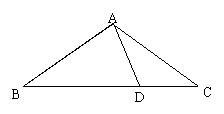
22、(6分)如图，在△ABC中,D是BC的中点，DE⊥AB,DF⊥AC,垂足分别是E、F，又DF=DE,请判定△ABC的形状,并说明理由。
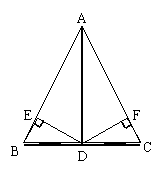
23、(6分)如图所示，在△ABC中，AB=BD=AC,AD=CD,求∠ADB的度数。
24、(7分)如图，已知B、F、C、E在同一条直线上，BF=CE,AB=DE,AB⊥AC,DE⊥DF,
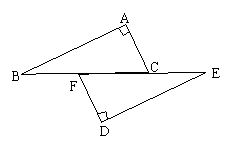求证：AB∥DE.
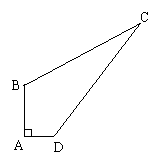
25、（8分）如图所示，AD=3,AB=4,∠A=90°,BC=12,CD=13,求四边形ABCD的面积。
 |
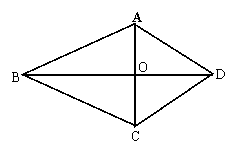
26、（8分）如图，四边形ABCD满足AB=CB,DA=DC,关于其对角线AC、BD,甲、乙、丙三位同学有如下说法：甲同学：“互相垂直”；乙同学：“互相平分”；丙同学：“互相垂直平分”，你认为那位同学的说法正确？请你证明。
 |
27、（11分）如图，在△ABC中，AB=AC,
⑴作AB的垂直平分线DE,交AB于点D,交AC于点E,连接BE.
(尺规作图,不写作法,保留作图痕迹)
⑵在⑴的基础上，若∠C=70°,求∠BEC的度数。
⑶在⑴的基础上，若AB=8,△BCE的周长为14，求BC长。
 |
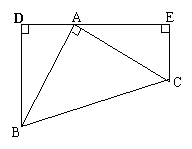
28、（6分）如图，已知BD⊥DE,CE⊥DE,垂足分别是D、E，AB=AC, ∠BAC=90°,试探索
DE、BD、CE长度之间的关系，并说明你的结论的正确性。
 |
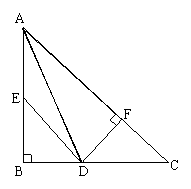
29、（6分）已知，如图，在△ABC中, ∠B=90°,AD为∠BAC的平分线，DF⊥AC,垂足为点F,
DE=DC,求证：BE=CF.
 |
30、（8分）如图，在△ABC中，AB=AC,P是BC上一点，PE⊥AB, PF⊥AC,垂足为E、F,BD是等腰三
角形腰AC上的高，
⑴求证：BD=PE＋PF.
⑵当点P在BC边的延长线上时，而其它条件不变，又有什么样的结论呢？请用文字加以说明本题的结论。
 |