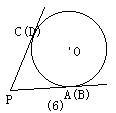综合题训练：
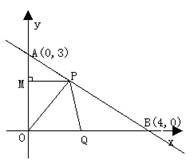一、已知：Rt△AOB中，∠AOB=900，OA=3厘米，OB=4厘米。以O为坐标原点建立如图所示的平面直角坐标系。设P、Q分别为AB边、OB边上的动点，它们同时分别从点A、O向B点匀速移动，移动的速度都为1厘米/秒。设P、Q移动时间为t秒（0≤t≤4）.
(1)过点P作PM⊥OA于M，证明：
，并求出P点的坐标（用t表示）
(2)求△OPQ的面积S（厘米2）与移动时间t（秒）之间的函数关系；当t为何值时，S有最大值，并求出S的最大值。
(3)当t为何值时，△OPQ为直角三角形？
(4) ①试证明无论t为何值，△OPQ不可能为正三角形；
②若点P的移动速度不变，试改变点Q的运动速度，
使△OPQ为正三角形，求出点 Q的运动速度和此时的t值。
二、已知抛物线y=x2-(2m+1)x+m2-1与x轴有公共点。（1）求m的取值范围。
(2)设抛物线与x轴交于A（x1,0), B(x2,0)两点(其中x2>x1>0);与y轴交于点C，
若AC·OC=BC·OA（O为原点），试求m的值，并求出这时抛物线的对称轴L。
(3)试问在抛物线y=x2-(2m+1)+m2-1的所有对称轴中，是否存在两条直线L1和L2，它们
关于（2）中所确定的直线L对称，并且与L的距离之和最大？若存在，请求出这两条对称轴L1和L2，并求出它们与L的距离之和最大值；若不存在，请说明理由。
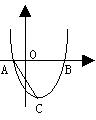三、如图：抛物线y=x2+bx+c与x轴交于点A、B，且点A、B在原点的两側，OA<OB，抛物线的顶点为C，连结AC。
（1）求b、c的取值范围；
（2）如果tg∠BAC=3,且
，求b、c的值；
（3）求出第（2）题中的抛物线上点A、B、C的坐标；
如果点P（x0,y0)在该抛物线上移动，且S△ABP>24，
求y0的取值范围。
四、已知：如图，在平面直角坐标系中，以点A（4，0）为圆心，AO为半径的圆交x轴于点B，设M为x轴上方的圆上一点，且 的长是
，
点P为 上任意一点（P不与O点重合），连结AP并延长交y轴于点C，连结BP并延长交y轴于点D，
（1）当点P在 上运动时，设PC=x, 
=y，
求y与x之间的函数关系式及自变量x的取值范围；
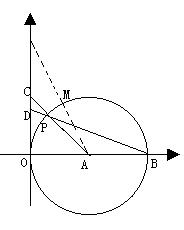（2）当P运动到某一位置时，恰使OB=3OD，求此时AC所在直线的解析式；
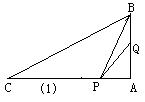
五、已知：如图，在△ABC中，∠A=900，AB=6，AC=8，点P从点A开始沿AC边向C匀速移动，点Q从点A开始沿AB边向点B，再沿BC边向点C匀速移动，若P、Q两点同时从点A出发，则可同时到达点C，
（1）如果P、Q两点同时从A出发，以原速度按各自的移动路线移动到某一时刻同时停止移动，当点Q移动到BC边上（Q不于C重合）时，求作以tg∠QCA、tg∠QPA为根的一元二次方程；
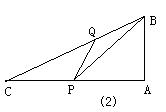
（2）如果P、Q两点同时从点A出发，以原速度按各自的移动路线到某时刻同时停止移动，当S△PBQ=
时，求PA的长。
六、
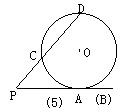
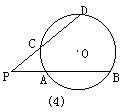
（1）经过⊙O内或⊙O外一点P作两条直线交⊙O于A、B和C、D四点（可能有重合的点），得到了如图所示的六种不同情况，在六种不同情况下，PA、PB、PC、PD四条线段之间在数量上满足的关系式可以用同一个式子表示出来，请你首先写出这个式子，然后只就图②所示的圆内两条弦相交一般情况，给出它的证明。
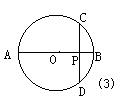
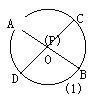
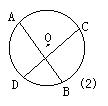（2）已知⊙O的半径为一定值，若点P是不在⊙O上的一个定点，请你过点P任意作一直线交⊙O于不重合的两点E、F，PE·PF的值是否为定值？为什么？由此你发现了什么结论？请你把这一结论用文字叙述出来
