 厦门市2003年初中毕业、升学统一考试
厦门市2003年初中毕业、升学统一考试
数 学 试 卷
(满分:A卷100分,B卷50分;考试时间120分钟)
注意:本试卷之一为A卷填空题、选择题和B卷的填空题。试卷之二为A卷填空题、选择题和B卷的填空题的答题表、A卷的解答题和B卷。考生必须把试卷之一试题的答案填在试卷之二相应的答题位置上,答在试卷之一上视为无效。
试卷之一(A卷填空、选择题)
一、填空题:(本大题共10小题,每小题 3分,共30分)(答案须填至试卷之二)
1.-2相反数是 ⑴ 。
2.已知∠A=30°,则∠A的补角是 ⑵ 度。
3.分解因式:mx+my= ⑶ .
4.化简:![]() = ⑷
.
= ⑷
.
5.点P(3,2)在第__⑸__象限.
 6.计算:
6.计算:![]() = ⑹ .
= ⑹ .
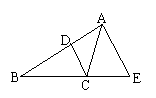
7.如图,CD平分∠ACB,AE∥DC交BC延长线于点E,
若∠ACE=80°,则∠BAC= ⑺ .
 8.厦门日报1月24日报道了2003年非师范类大中专毕业生和研究生(厦门生源)的就业形势,其中关于研究生学历的工作岗位是供不应求.具体情况是:实际需要研究生的人数比实际毕业的研究生的人数多1124人,它们之间的比是309:28.则实际需要的研究生___⑻___人,实际毕业研究生___⑻___人.
8.厦门日报1月24日报道了2003年非师范类大中专毕业生和研究生(厦门生源)的就业形势,其中关于研究生学历的工作岗位是供不应求.具体情况是:实际需要研究生的人数比实际毕业的研究生的人数多1124人,它们之间的比是309:28.则实际需要的研究生___⑻___人,实际毕业研究生___⑻___人.
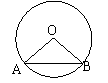
9.如图,在⊙O中,弦AB所对的劣弧为圆的![]() ,
,
圆的半径为4厘米,则AB= ⑼ 厘米.
10.某物体从上午7时到下午4时的温度M(![]() C)是时间t(小时)的函数,:
C)是时间t(小时)的函数,:
M=![]() (其中t=0表示中午12时,t=1表示下午1时),则上午10时此物体的温度为 ⑽
(其中t=0表示中午12时,t=1表示下午1时),则上午10时此物体的温度为 ⑽ ![]() C.
C.
二 选择题(本大题共6小题,每小题4分,共24分)
11.5的算术平方根是(⑾)
(A) ![]() . (B) -
. (B) -![]() . (C) ±
. (C) ±![]() . (D) 25.
. (D) 25.
12.不等式![]() 的解集是 (⑿).
的解集是 (⑿).
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
13.已知直角三角形中30![]() 角所对的直角边长是2厘米,则斜边的长是(⒀)
角所对的直角边长是2厘米,则斜边的长是(⒀)
(A) 2厘米 (B) 4厘米 (C) 6厘米 (D) 8厘米
14.化简![]() 的结果是(⒁)。
的结果是(⒁)。
(A) ![]() (B)
(B)![]() (C)
(C)
![]() (D)
(D)
![]()
15.在△ABC中,I是内心,∠BIC=130![]() ,则∠A的度数是(⒂)
,则∠A的度数是(⒂)
(A) 40° (B) 50° (C) 65° (D) 80°
16.已知以(-1,0)为圆心,1为半径的⊙M和抛物线![]() ,现有两个命题:⑴抛物线
,现有两个命题:⑴抛物线![]() 与⊙M没有交点.
与⊙M没有交点.
⑵将抛物线![]() 向下平移3个单位,则此抛物线与⊙M相交.则以下结论正确的是(⒃)
向下平移3个单位,则此抛物线与⊙M相交.则以下结论正确的是(⒃)
(A)只有命题⑴正确 (B)只有命题⑵正确
(C)命题⑴、⑵都正确 (D)命题⑴、⑵都不正确
 厦门市2003年初中毕业、升学统一考试
厦门市2003年初中毕业、升学统一考试
数 学 试 卷
(满分:A卷100分,B卷50分;考试时间120分钟)
试卷之二
| 题序 | 一 | 二 | 三 | A卷 | 全卷 | ||||||||
| 1~10 | 11~16 | 17 | 18 | 19 | 20 | 21 |
|
| |||||
| 得分 |
|
|
|
|
|
|
| ||||||
| 题序 | 四 | 五 | B卷 | ||||||||||
| 22~25 | 26 | 27 | 28 | 29 |
| ||||||||
| 得分 |
|
|
|
|
| ||||||||
| |||||||||||||
A 卷
一.填空题答题表:(本大题有10小题,每小题3分,共30分)
1. . 2. 度. 3. .4 . .5.第 象限.
6. . 7. 度.8. 实际需要的研究生___ __人,实际毕业的研究生__ ___人. 9. 厘米. 10. .
二.选择题: (本大题共6小题,每小题 3分,共18分)
| 题序 | 11 | 12 | 13 | 14 | 15 | 16 |
| 选项 |
三 解答下列各题:(第17、18题每题8分,第19、20、21题每题10分,共46分)
17.(本题满分8分)先化简,再求值。
![]() 其中
其中![]() ,
,![]()
18.(本题满分8分)已知:如图AC和BD相交于O,AB∥CD,OA=OC.
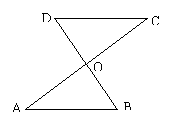 求证:△AOB≌△COD.
求证:△AOB≌△COD.
19.(本题满分10分)某中学要召开运动会,决定从初三年全部的150名的女生中选30人,组成一个彩旗方队(要求参加方队的同学的身高尽可能接近).现在抽测了10名女生的身高,结果如下(单位:厘米):166 154 151 167 162 158 158 160 162 162
⑴依据样本数据估计,初三年全体女生的平均体高约是多少厘米?
⑵这10名女生的身高的中位数、众数各是多少?
⑶请你依据样本数据,设计一个挑选参加方队的女生的方案?
20.(本题满分10分)如图,BD、BE分别是∠ABC和它的邻补角∠ABP的平分线,
AE⊥BE,AD⊥BD,E、D为垂足.
⑴求证:四边形AEBD是矩形.
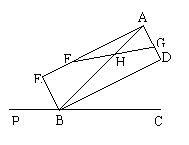 ⑵若
⑵若![]() ,F、G分别为AE、AD上的点,FG交AB于点H,且
,F、G分别为AE、AD上的点,FG交AB于点H,且![]() ,
,
求证:AHG是等腰三角形.
21.(本题满分10分)已知平面坐标系上有6个点:
A(3,3),B(1,1),C(9,1),D(5,3),E(-1,-9),F(-2,![]() ).
).
下面有两个小题:
⑴请将上述的6个点按下列的要求分成两类,并写出同类点具有而另一类点不具有的一个特征(请将答案按下列要求写在横线上:特征不能用否定形式表述,点用字母表示);
①甲类含两个点,乙类含其余四个点.
甲类:点 , 是同一类点,其特征是 .
乙类:点 , , , 是同一类点,其特征是 .
②甲类含三个点,乙类含其余三个点.
甲类: 点 , , 是同一类点,其特征是 .
乙类:点 , , 是同一类点,其特征是 .
⑵判断下列命题是否正确,正确的在括号内打“√”,并说明理由;错误的在括号内打“×”,并举反例说明.
①直线y=-2x+11与直线AD没有交点. ( )
②直线y=-2x+11将四边形ABCD分成面积相等的两部分. ( )
(如需要,可在坐标系上作出示意图)
B 卷
四 填空题:(本大题共4小题,每小题4分,共16)
22.已知⊙O的半径为R,则与⊙O相内切且半径为r(r<R)的点的轨迹
是 .
23.高30厘米的圆柱形蒸汽锅炉,它的底面直径是20厘米,如果蒸汽锅炉内每平方厘米所承受的蒸汽压力是15牛顿,那么这个蒸汽锅炉内部表面所受的蒸汽压力是 牛顿.
24.阅读下面的例题:
解方程![]()
解:⑴当![]() 时,原方程可化为
时,原方程可化为![]() ,解得:
,解得:![]() (不合,舍去)
(不合,舍去)![]() .
.
⑵当![]() 时,原方程可化为
时,原方程可化为![]() ,解得:
,解得:![]() (不合,舍去)
(不合,舍去)![]() .
.
∴
原方程的根是![]() ,
,![]() .
.
请参照例题解方程![]() ,则此方程的根是
.
,则此方程的根是
.
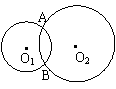 25.如图,⊙O1、⊙O2相交于A、B两点,给出四个命题:
25.如图,⊙O1、⊙O2相交于A、B两点,给出四个命题:
⑴若AC是⊙O2的切线且交⊙O1于点C,AD是⊙O1
的切线且交⊙O2于点D,则AB2=BC·BD.
⑵连AB、O1O2,若O1A =15cm,O2A=20cm,
AB=24cm,则=25cm.
⑶若CA是⊙O1的直径,DA是⊙O2的一条非直径的弦,且点D、B不重合,则C、B、D三点不在同一直线上.
⑷若过点A作⊙O1的切线交⊙O2于点D,直线DB交⊙O1于点C,直线CA交⊙O2于点E,连结DE,则DE2= DB·DC.
则正确命题的序号是 .(在横线上填上所有正确的序号)
五 解答下列各题(第26、27、28题每题8分,第29题10分,共34分)
26.(本题满分10分)已知抛物线![]() ,
,
⑴求证:此抛物线与x轴有两个不同的交点.
⑵设![]() 、
、![]() 是此抛物线与x轴有两个交点的坐标,且满足
是此抛物线与x轴有两个交点的坐标,且满足![]() +
+![]() =
=![]() .
.
① 求抛物线的解析式.
②设点P(m1,n1)、Q(m2,n2)是抛物线上两个不同的点,且关于此抛物线的对称轴对称,求m1+m2的值.
|
|
(1)设BC的长为m1,OD的长为m2,求证:m1=m2.
 (2)若BD与⊙O1相切,求证:BC=
(2)若BD与⊙O1相切,求证:BC=![]() AD.
AD.
28.(本题满分10分)某工厂拟建一座平面为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每平方米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)
⑴当三级污水处理池的总造价为47200元时,求池长x.
![]()
![]()
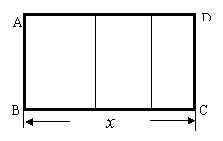 ⑵如果规定总造价越低就越合算,那么根据题目提供的信息,以47200元为总造价来修建三级污水处理池是否最合算?请说明理由.
⑵如果规定总造价越低就越合算,那么根据题目提供的信息,以47200元为总造价来修建三级污水处理池是否最合算?请说明理由.
31.已知一次函数![]() 的图象经过第一、二、三象限,且与x、y轴分别交于A、B两点,O是原点,若△ABC的面积为2,
的图象经过第一、二、三象限,且与x、y轴分别交于A、B两点,O是原点,若△ABC的面积为2,
(1)求一次函数的解析式.
(2)设点P(m,n)(其中n≥0)是一次函数![]() 的图象上的点,过点P向以原点O为圆心,1为半径的⊙O引切线PC、PD,切点为C、D,
的图象上的点,过点P向以原点O为圆心,1为半径的⊙O引切线PC、PD,切点为C、D,
①当![]() 时,求四边形PCOD的面积S的取值范围.
时,求四边形PCOD的面积S的取值范围.
②若CD=![]() ,求切点C、D的坐标.
,求切点C、D的坐标.
(如需要,可在坐标系上作出示意图)