2004年青岛市中考数学试题
一、选择题（3×8＝24分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 |
1. 小明设计了一个关于实数运算的程序：输入一个数后，输出的数总是比该数的平方小1，小刚按照此程序输入
后，输出的结果应为（ ）
A：10 B：11 C：12 D：13
2.用换元法解方程
时，若设x2+x=y, 则原方程可化为（ ）
A：y2+y+2=0 B：y2－y－2=0 C：y2－y+2=0 D：y2+y－2=0
3. 下列图形中，是中心对称图形，但不是轴对称图形的是（ ）
A：正方形 B：矩形 C：菱形 D：平行四边形
4.两年期定期储蓄的年利率为2.25％，按照国家规定，所得利息要缴纳20％的利息税，王大爷于2002年6月存入银行一笔钱，两年到期时，共得税后利息540元，则王大爷2002年6月的存款额为（ ）元
A：20000 B：18000 C：15000 D：12800
5.生物学指出：在生态系统中，每输入一个营养级的能量，大约只有10％的能量能够流动到下一个营养级，在H1→H2→H3→H4→H5→H6这条生物链中（Hn表示第n个营养级，n=1,2,3,4,5,6），要使H6获得10千焦的能量，需要H1提供的能量约为（ ）千焦。
A： 106 B： 105 C： 104 D： 103
6、如图，E、F、G、H分别是四边形ABCD四条边的中点，要使EFGH为矩形，四边形应该具备的条件是（ ）
A：一组对边平行而另一组对边不平行
B：对角线相等
C：对角线相互垂直
D：对角线互相平分
7、函数y=－ax+a与y=
（a≠0）在同一个坐标系中的图像可能是（ ）
8、某次“迎奥运”知识竞赛中共有20道题，对于每一道题，答对了得10分，答错了或者不答扣5分，至少要答对（ ）道题，其得分才会不少于95分。
A；14 B：13 C：12 D：11
二、填空题（3×8＝24分）
9、化简：
（a<2）＝
。
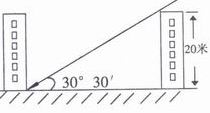
10、青岛位于北纬36°4′，可以通过计算求得：在冬至日正午时分的太阳入射角为30°30′，因此，在规划建设楼高为20米的小区时，
两楼间的最小距离为 米才能够保证不挡光。
（结果保留4 个有效数字，sin30°30′＝0.5075, tan30°30′=0.5890）
11、下表是某报纸公布的我国“九五”期间国内生产总值（GDP）的统计表，那么这几年间我国国内生产总值平均每年比上一年增长 万亿元。
| 年份 | 1996 | 1997 | 1998 | 1999 | 2000 |
| GDP(万亿元) | 6.6 | 7.3 | 7.9 | 8.2 | 8.9 |
12、2003年10月15日，航天英雄杨利伟乘坐“神州五号”载人飞船，于9时9分50秒准确进入预定轨道，开始巡天飞行，飞船绕地球飞行了14圈后，返回舱与推进舱于16日5 时59分分离，结束航天飞行，飞船共用了20小时49分10秒，飞行了约6×105km，则“神州五号”飞船的平均飞行速度约为 km/s （结果精确到0.1）
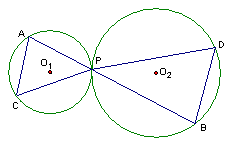13、已知如图：⊙O1与⊙O2外切于点P, 直线AB经过点P交⊙O1于A，交⊙O2于B，点C、D分别为⊙O1、⊙O2上的点，且∠ACP=65°，则∠BDP＝ 。
14、生物学研究表明：某种蛇的长度y(cm)是
其尾长x(cm)的一次函数，当蛇的尾长为6cm
时，蛇长为45.5cm；当尾长为14cm时，蛇长
为105.5cm，当一条蛇的尾长为10cm时，
这条蛇的长度是 cm。
15、已知：在等腰梯形ABCD中，AD//BC,
对角线AC⊥BD, AD=3cm, BC=7cm。则梯形的高是 cm。
16、观察下列由棱长为1的小立方体摆成的图形，寻找规律：
如图1中：共有1 个小立方体，，其中1个看得见，0个看不见；如图2中：共有8个小立方体，其中7个看得见，1个看不见；如图3中：共有27个小立方体，其中有19个看得见，8个看不见；……，则第6个图中，看不见的小立方体有 个。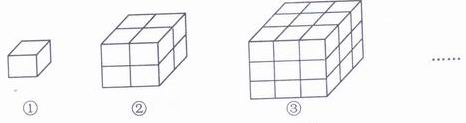
三、作图题（满分6分）
17、如图，AB、CD是两条相互垂直的公路，设计时想在拐弯处用一段圆弧形湾道把它们连接起来（圆弧在A、C两点处分别与道路相切），测得AC＝60米，∠ACP＝45°。
（1） 在图中画出圆弧形弯道的示意图；
（2） 
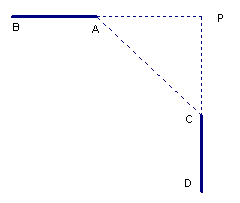求弯道部分的长。（结果保留四个有效数字）
四、解答题（本题满分66分，共有9道小题）
18、本小题满分6分
已知方程5x2+kx－10＝0的一个根是－5，求它的另一个根及k的值。
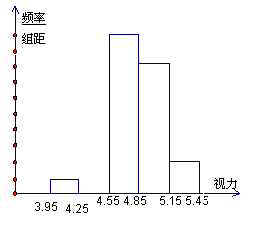19、（本题满分6′）青少年视力水平下降已经引起全社会的广泛关注，为了了解某市初中毕业生5000名学生的视力情况，我们从中抽取了一部分学生的视力作为样本进行数据处理，得到如下的频率分布表和频率分布直方图（部分）：
| 分组 | 频数 | 频率 |
| 3.95～4.25 | 2 | 0.04 |
| 4.25～4.55 | 8 | 0.16 |
| 4.55～4.85 | 0.40 | |
| 4.85～5.15 | 16 | 0.32 |
| 5.15～5.45 | 4 | 0.08 |
| 合计 | 1 |
①.根据上述数据，补全频率分布表与频率分布直方图
②.若视力在4.85以上属于正常，不需要矫正，试估计该市5000名初中毕业学生中约有多少名学生的视力需要矫正？
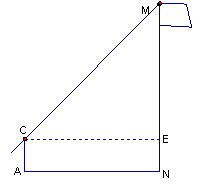20、（本题满分6分）在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案（如图1所示）：
（1） 在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE＝α ；
（2） 量出测点A到旗杆底部N的水平距离AN＝m;
（3） 量出测倾器的高度AC＝h。
根据上述测量数据，即可求出旗杆的高度MN。
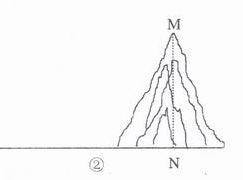
如果测量工具不变，请仿照上述过程，设计一个测量
某小山高度（如图2）的方案：
1） 在图2中，画出你测量小山高度MN的示意图
（标上适当的字母）
2）写出你的设计方案。 （图1）
21、（本题满分6分）
某市今年1月1日起调整居民用水价格，每立方米水费上涨25％。小明家去年12月份的水费是18元，而今年5月份的水费是36元。已知小明家今年5月份的用水量比去年12月份多6m3，求该市今年用水的价格。
22、（本题满分8分）
已知：在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q。
1） 求四边形AQMP的周长。
2） 写出图中的两对相似三角形（不需证明）。
3） M位于BC的什么位置时，四边形AQMP为菱形？
说明你的理由。
23、（本题满分8分）四边形是我们大家最熟悉的图形之一，我们已经发现了它的许多性质，只要善于观察、乐于探索，我们还会发现更多的结论。
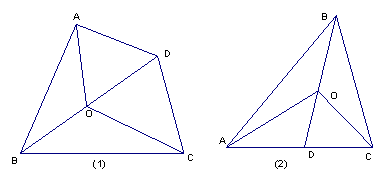
1）四边形的一条对角线上任意一点与另外两个顶点的连线，将四边形分成四个三角形（如图1）其中相对的两个三角形的面积之积相等，你能够证明这个结论吗？试试看。
已知：四边形ABCD中，O是对角线BD上任意一点，（图1）
求证：
2)在三角形中（如图2），你能否归纳出类似的结论，若能够，写出你猜想的结论，并证明；若不能够，说明理由。
24、（本题满分8分）
某工厂现有80台机器，每台机器平均每天生产384件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，由于其它生产条件不变，因此每增加一台机器，每台机器平均每天将少生产4件产品。
1） 如果增加x台机器，每天的生产总量为y件，请写出y与x的函数关系式。
2） 增加多少台机器，可以使每天的生产总量最大？最大生产总量是多少？
25、（本题满分8分）
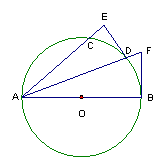如图AB为⊙O的直径，D是弧BC的中点，DE⊥AC交AC的延长线于E，⊙O的切线BF交AD的延长线于F。
1） 求证：DE是⊙O的切线。
2） 若DE＝3，⊙O的半径是5，求BF的长。
26、（本题满分10分）
把两个全等的等腰直角三角板ABC与EFG（其直角边长都为4）叠放在一起，（如图①）
且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合。现将三角板EFG绕O点顺时针旋转（旋转角α满足0°＜α＜90°），四边形CHGK是旋转过程中两个三角板的重叠部分（如图②）
1） 在上述旋转过程中，BH与CK有怎样的数量关系？四边形CHGK的面积有何变化？证明你发现的结论。
2） 连接HK，在上述旋转过程中，设BH=x, △GKH的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围。
3） 在2）的前提下，是否存在某一位置，使△GKH的面积恰好等于△ABC的面积的
？若存在，求出此时x的值；若不存在，说明理由。
2004年青岛中考数学试题参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | B | D | D | C | A | C | A | B |
二、填空题
| 题号 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | －1 | 33.96 | 0.575 | 8.0 | 65° | 75.5 | 5 | 125 |
三、作图
四、18、
