2004年中考数学模拟试题
一、选择题：
1．两圆内切，圆心距为8，若一圆的直径为6，则另一圆的直径为（ ）。
A．2 B．5 C．10 D．14
2．有4张牌分别是A、A、K、Q，牌面朝下，同时翻开两张，两张都是A的概率是（ ）。
A．1/4 B．1/6 C．1/8 D．1/16
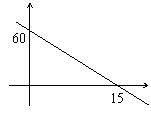
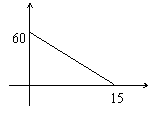
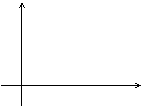
3．汽车在行驶中，油箱中有油60升。如果每小时耗油4升，那么油箱中含油量y（升）与行驶时间t（小时）的函数关系式用图象表示为（ ）。
A． B．
 |  |
|
|
|
|
C．
D．
4．观察下列“风车”的平面图案：
 |  | ||
其中是中心对称图形的有
A．1个 B．2个 C．3个 D．4个
5．给出下列程序
输入x
立方 ×k +b 输出
且当输入1时，输出值为3；输入0时，输出值为2。
则当输入x值为-1时，输出值为 。
A．1 B．-1 C．0 D．2
6．如图，从位于O处的某海防哨所发现在它的北偏东60°的方向，相距600米的A处有一艘快艇正在向正南方向航行，经过若干时间快艇要到达哨所东南方向的B处，则A、B间的距离是（ ）米。
A．300+300√3 B．300+300√2 C．150+150√3 D．150+150√2
二、填空题：
7．方程x2-6x-2=0的解是 。
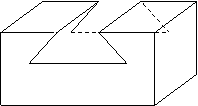
8．画出几何体的俯视图、左视图。
 |  | | |||||
 | |||||||
9．中超足球比赛中，贝莱特队首轮上场，队员的年龄如下表：
| 年龄 | 20 | 22 | 23 | 25 | 28 | 30 | 32 |
| 人数 | 1 | 2 | 1 | 3 | 2 | 1 | 1 |
则上场队员的众数为 ，平均年龄为 。
10．粮堆底面周长为15.7cm，高为1.5cm，要用塑料布盖住整个粮堆，至少要 m2塑料布。
11．一定质量的氧气，它的密度ρ（kg/m3）是它的体积V（m3）的反比例函数，当V=10 m3时，ρ=1.43 kg/m3。写出ρ与V的函数关系式 ，当V=2 m3时，氧气的密度ρ= 。
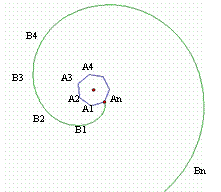
12．如图，正多边形A1、A2、A3、A4……An，
曲线B1、B2、B3、B4……Bn叫做“正多边形的
渐开线”，其中AnB1、B1B2、B2B3、B3B4……
的圆心依次按A1、A2、A3、A4……循环。循环一
周就叫一周曲线长，当A1A2=1时，一周曲线长为
。
三、作图题：
13．（1）三角形外心是 的交点。
|
|
（2）A、B、C是三个放牧点，要修建一个牧民定居点，使三个放牧点到定居点的距离相等。
 |
四、解答题：
14．某校队组织学生野外游玩，当晚住宿时，若3个同学住一个帐篷，有5人没地方住。若每个帐篷住4人，则最后一个帐篷不足两人。问有几间帐篷，有几个学生？
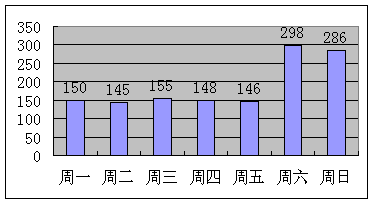
15．小红的奶奶在公园里卖冷饮，小红对奶奶一星期每天卖冰糕的数量、品种进行统计如下。
|
|
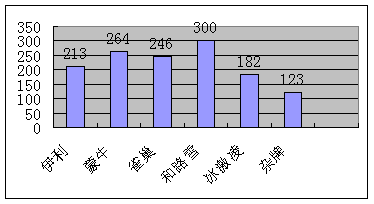
⑴求出一周七天卖冰糕的中位数、平均数。
⑵每天卖冰糕的平均数，能否反映真实水平？请说明理由。
⑶请为奶奶的进货提出合理化的建议：
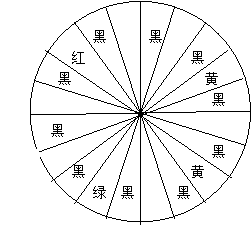16．小明和小亮一天在广场上玩，看见有人在设摊“摸彩”。
规则如下：不花钱就可以转，转到红色奖5元，转
到绿色奖2元，转到黄色奖1元，白色不交钱，
黑色给摊主1元钱。小明认为：不花钱就可以玩游
戏，游戏者上算；小亮却认为：摊主不会让人那么
容易占便宜。可又说不出道理。你能用学过的概率
知识帮他解决吗？
17．⑴某校课外数学小组要测量校园内的旗杆，现有米尺一把，不可以爬上旗杆，你可以再选一件或工件工具（也可不选）设计一个测量方案，并画出草图。
|
|
|
|
⑵小明、小亮是一个活动小组，他们没有选用其它工具，而是这样做的，小明站在杆影下，让头顶的影子恰好与杆顶的影子重合。小亮测得旗杆到小明的距离为5.7米，小明到影子顶端的水平距离为2.3米，请你帮他们求求旗杆的高度。（精确到0.1米）
18．某商场用5万元购进一批儿童玩具，加价30%销售，很快脱销，商场决定再进一批。因材料涨价，所以该玩具比进货价每件贵2元。第二次用10.8万元购进第一批数量的2倍，当商场卖到一半时发现该玩具销量收益下降。所以决定以原价的八五折售出，很快售完。
⑴问2次共购进多少间玩具？
⑵商场卖这种玩具共盈利多少元？
|
|
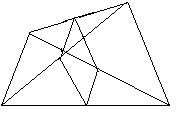⑴四边形EFGH是什么四边形？请证明。
|
|
|
⑵四边形ABCD有什么条件时，四边形EFGH是菱形？
|
| ||||||
| |||||||
⑶四边形EFGH可能是正方形吗？
20．某旅行社组团去外地旅游，20人一起组团，每人单价为1200元。如果每团超过20人时，给予优惠，每增加一人，单价减少20元。
⑴设旅行社每团营业额为y元，人数为x人。则每团人数为多少时，旅行社可获得最大营业额？
⑵若该旅行社组团费用Q=6x2+18000，那么为获得最大利润，每团有多少人最适宜。
 |
|
⑴若点E在BC上运动（E与B、C不重合），点F在CA上
运动，且EF平分△ABC的周长，设CE=x，△CEF的面积
为
|
|
1）x=3时，求y的值
2）求y与x之间的函数关系式，并写出自变量的取值
|
3）以E为圆心，EC为半径作一个圆。试问：当x为何值时，此圆与AB相切
22．如图，这些等腰三角形与正三角形的形状有差异，我们把这与正三角形的接近程度称为“正度”。在研究“正度”时，应保证相似三角形的“正度”相等。
|
设等腰三角形的底和腰分别为a、b，底角和顶角分别为α，β。要求“正度”的值是非负数。
 |
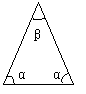同学甲认为：可用式子a-b来表示“正度”，a-b的值越小，表示等腰三角形越接近正三角形；
同学乙认为：可用式子α-β来表示“正度”，α-β的值越小，表示等腰三角形越接近正三角形；
探究：⑴他们的方案哪个较合理，为什么？
⑵对你认为不够合理的方案，请加以改进（给出式子即可）；
⑶请再给出一种衡量“正度”的表达式。