中考数学模拟试题3-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载

中考数学模拟试题（3）

卷Ⅰ（选择题，共20分）

一、　　　　 选择题:（本大题共10个小题，每小题2分，共20分）

1．　小李用计算机编写了一个计算程序，输入和输出的数据关系如下表

输入	…	1	2	3	4	5	…
输出	…	2	5	10	17	26	…

当输入数据是6时，输出的数据是（　）

A．　30　　B．　33　C．　36　　D． 37

2．红星中学初三（2）班十几名同学毕业前和数学老师合影留念，一张彩色底片要0.6元，扩印一张相片0.5元，每人分一张，免费赠送老师一张（由学生出钱），每个学生交0.6元刚好，相片上共有多少人（　　）

A．13个　 B．12个　 C．11个　 D．无法确定

3．下列四个函数：（1）y =3x-1; （2）y=; （3）y=2x²; （4）y=2x (-1≤x≤2)，其中图像是中心对称图形，且对称中心是原点的共有（　　）

A 1个; B. 2 个;　　C. 3个;　D. 4个

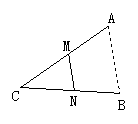
4．如图，A、B两点分布在水池的两边，一学生在AB外选取了一点C，连接AC和BC，并分别找出各自中点M、N，若测得MN=20m,则A、B两点的距离为（　　）

A．25　　B．30　　 C．35　　 D．40

5．若点（-5，y₁）、(-3,y₂)、(3,y₃)都在反比例函数y= -的图像上，则（　　）

A．y₁＞y₂＞y₃　　　　 B．y₂＞y₁＞y₃　　

C．y₃＞y₁＞y₂　　　　D．y₁＞y₃＞y₂

6．一个滑轮起重装置如图所示，滑轮的半径是15cm，当重物上升15cn时，滑轮的一条半径OA绕轴心O按顺时针方向旋转的角度约为（　）（π取3.14，结果精确到1º）

A．115º　　　　B．60º 　　　 C．57º　　　D．29º

7．三峡工程在6月1日于6月10日下闸蓄水期间，水库水位由106米升至135米，高峡平湖初现人间，假设水库水位匀速上升，那么下列图象中，能正确反映这10天水位h（米）随时间t（天）变化的是（　　）

8．已知方程x²-3x+1=0，求作一个一元二次方程使它的根分别是原方程各根的倒数，则这个一无二次方程是（　　）

　　 A．x²+3x+1=0; B．x²+3x-1=0　

C．x²-3x+1=0 　D．x²-3x-1=0

9．如图，BD＝CD，AE：DE＝1：2，延长BE交AC于F，且AF＝4cm，则AC的长为（　　）

A、24cm　 B、20cm　 C、12cm　 D、8cm

10．红星中学新实验楼铺设地面，已有正三角形形状的地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则该学校不应该购买的地砖形状是（　　）

A、正方形　　　 B、正六边形　　 C、正八边形　　 D、正十二边形

卷II（非选择题，共100分）

二、填空题：本大题共10个小题；每小题2分，共20分．把答案写在题中横线上．

11．0.25×（-）^-2 +（- ）⁰ = 　　　　 .

12．2004年全国财政收入达2.63万亿元，这比2003年增长了21.4%，用科学记数表表示2003的全国财政收入是　　　　　　　　　　　　元（结果保留3个有效数字）　

13．已知不等式组的解集是2<x<3,分解因式x²-3x-2mn=　　　　　　　　．

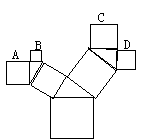
14．如图是一个艺术窗的一部分，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为5cm，则正方形A、B、C、D的面积和是　　　　　　．

15．写出一个只含字母a的代数式（要求：（1）要使此代数式有意义，字母a必须取全体负数；（2）此代数式的值恒为负数）：　　　　　　　　　。

16．如图，PA、PB、DE分别切圆O于点A、B、C，如果PO=10cm，ΔPDE的周长为12cm，那么圆O的半径为　　　　　；

17．某商场销售一批电视机，一月份每台毛利润是售出价的20％（毛利润＝售出价－买入价），二月份该商场将每台售出价调低10％（买入价不变），结果销售台数比一月份增加120％，那么二月份的毛利润总额与一月份毛利润总额的比是　　　　。

18．若x为的倒数，则的值为　　　　。

19．已知m、n是方程的两根，则与的积是　　　　。

20．已知甲船在A处，乙船在甲船的正南方向的B处，甲船由A处向北偏西方向行驶，同时乙船由B处向正北方向行驶，半小时到C处，此时甲船在乙船的北偏西方向，距乙船海里的D处，甲船每小时行驶　　　　海里。

三、解答题：(本大题共8个小题；共80分．解答应按要求写出文字说明、或证明过程或演算步骤)．

21．(本小题满分8分)

化简:- ，并任选一组你认为合适的x、y的值代入求值。

22．(本小题满分8分)

如图，正方形ABCD中，E、F分别是AB和AD上的点，已知CE⊥BF，垂足为M，请找出和BE相等的线段，并证明你的结论。

23．(本小题满分8分)

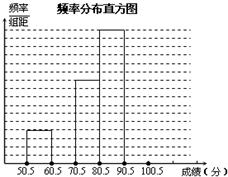
为了让学生了解环保知识，增强环保意识，红星中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：
　（1）填充频率分布表中的空格；

（2）补全频率分布直方图；

（3）在该问题中的样本容量是多少？

答：　　　　　　　　　　　　　　　　　。

（4）全体参赛学生中，竞赛成绩落在哪组范围内的人数最多？（不要求说明理由）”

答：　　　　　　　　　　　　　　　　　　。

（5）若成绩在90分以上（不含90分）为优秀，则该校成绩优秀的约为多少人？答：　　　　　　　　　　　　　　　　　　　。

24．(本小题满分8分)

如图：矩形ABCD的顶点B、C在x轴的正半轴上，A、D在抛物线上，矩形的顶点均为动点，且矩形在抛物线与轴围成的区域里。

（1）设A点的坐标为（，），试求矩形周长关于变量的函数表达式；

（2）是否存在这样的矩形，它的周长为9，试证明你的结论。

25．(本小题满分8分)

国庆节，甲、乙两班学生到集市上购买苹果，，苹果的价格如下：

购苹果数	不超过30千克	30千克以上但不超过50千克	50千克以上
每千克价格	3元	2.5元	2元

甲班分两次共购买苹果70千克（第二次多于第一次），共付出189元，而乙班则一次购买苹果70千克。

（1）乙班比甲班少付多少元？

（2）甲班第一次、第二次分别购买苹果多少千克？

26．(本小题满分8分)

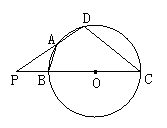
如图,四边形ABCD内接于以BC为直径的圆O，且AB＝AD，延长CB、DA交于P，当PB＝BO，CD＝18时，求：

（1）⊙O的半径长；（2）PA的长。

27．(本小题满分8分)

已知，△ABC的两边AB、AC的长是关于x的一元二次方程x²- (2k+3)x+k²+3k+2=0的两实根，第三边BC的长为5。

问：（1）k为何值时，△ABC是以BC为斜边的直角三角形。

（2）k为何值时，△ABC是等腰三角形，并求△ABC的周长。

28．（本题满分12分）

已知，如图，a，b，c分别是ΔABC中∠A，∠B，∠C的对边，P为BC上一点，以AP为直径的圆O交AB于D，PE∥AB交AC于E，b，c是方程x²+kx+9=0的两根，且（b²+c²）（b²+c²－14）－72=0，锐角B的正弦值等于。（1）求K的值；（2）设BD=x，求四边形ADPE的面积为S关于x的函数关系式；（3）问圆O是否能与BC相切？若能请求出x的值；若不能，请说明理由。