中考数学模拟试题（4）
说明：本试卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷满分为100分，第Ⅱ卷满分为50分，共150分，全卷共九大题。
第Ⅰ卷
一、选择答案（本题共有18小题，每小题满分2分，共36分）注意：每小题有四个选项，其中有且仅有一项是符合题意的。所有选择题必须在答案卡上用规定的铅笔作答，选错、不选、多选或涂改不清的，均不给分。
1．5的平方根是（ ）。
（A）25
（B）
（C）
（D）
2．设甲数是
，若甲数是乙数的2倍，则乙数是（ ）。
（A）
（B）
（C）
（D）
3．下列函数中,自变量的取值范围为x≥3的是（ ）。
（A）
（B）
（C）
（D）
4．若0＜a＜1，则点M（a－1，a）在（ ）。
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
5．不等式组
的解集为（ ）。
（A）＜1
（B）＞2
（C）＜1或＞2
（D）1＜＜2
6．已知a＞b，则下列不等式中，正确的是（ ）。
（A）―3a＞―3b
（B）
＞
（C）3－a＞3－b
（D）a－3＞b－3
7．下列运算中，正确的是（ ）。
（A）
（B）
（C）
（D）
8．若数据80，82，79，69，74，78，81，的众数是82，则（ ）。
（A）=79 （B）=80 （C）=81
（D）=82
9．已知某5个数的和是a，另6个数的和是b，则这11个数的平均数是（ ）。
（A）
（B）
（C）
（D）
10．函数y=－的图象与函数y=＋1的图象的交点在（ ）。
（A）第一象限（B）第二象限（C）第三象限 （D）第四象限
11．下列方程中，无实数根的方程是（ ）。
（A）
（B）
（C）
（D）
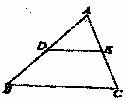12．如图，若DE是△ABC的中位线，△ABC的周长为1，则△ADE的周长为（ ）。
（A）
（B）
（C）
（D）
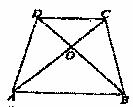
13．如图，在等腰梯形ABCD中，AB∥DC，AC和BD相交于点O，则图中的全等三角形共有（ ）。
（A）1对
（B）2对
（C）3对 （D）4对
14．计算：tan45°＋sin30°＝（ ）。
（A）2 （B）
（C）
（D）
15．在△
（ ）。
（A）
（B）
（C） （D） 
16．底面半径为5,高为10的圆柱的侧面积为（ ）。
（A）50π （B）100π （C）125π （D）250π
17．如图，正方形ABCD内接于⊙O，点P在弧 AD上，则∠BPC（ ）。
（A）35°
（B）40°
（C）45°
（D）50°
18．若两圆有且只有两条公切线,则这两圆的位置关系是（ ）。
（A）外离 （B）外切 （C）相交 （D）内切
二、填空（本题共有7小题，每小题满分2分，共14分）
19．0.000018用科学记数法表示为___ __.
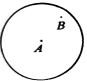
20．如图，以A、B两点为其中两个顶点作位置不同的等边三角形，最多可以作出_____个.
21．用换元法解方程
__
___.
22．化简
得___ __.
23．半径为6cm，圆心角为60°的扇形的面积为___ __cm2.（答案保留π）
24．把
化为
（其中h、k是常数）的形式是__ ___.
25．抛物线
的顶点坐标是_____.
三、（本题满分6分）
26．如图，已知线段a、b。
求作：（1）Rt△ABC，使
（2）△ABC的角平分线CD和经过点A、C、D的⊙O.（作CD和⊙O不要求写作法，但要保留作图痕迹）
四、（本题共有4小题，第1小题满分5分，第2、3小题满分各6分，第4小题满分7分，共24分）.
27．计算
.
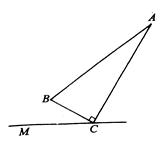28．如图,
求sin
和点B到直线MC的距离.
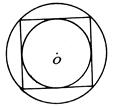29．如图，已知正方形的边长是4cm，求它的内切圆与外接圆组成的圆环的面积.（答案保留π）
30．某车间一月份生产零件7000个，三月份生产零件8470个，该车间这两个月生产零件平均每月增长的百分率是多少？
五、（本题满分10分）
31．解方程
六、（本题满分10分）
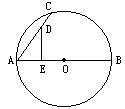
32．如图，已知AB是⊙O的直径，点D在弦AC上，DE⊥AB于E.求证：
第Ⅱ卷
七、（本题共有4小题，第1、2小题满分各6分，第3、4小题满分各8分，共28分）
33．已知二次函数的图象经过点（－1，－5），（0，－4）和（1，1）.求这个二次函数的解析式.
34．如图，PB是⊙O的割线，点A、B是它与⊙O的交点，PO交⊙O于点C，AB = 4，PA = 6，PC = 4求OC.
35．已知关于的方程
的两实根互为倒数，求a的值.
36．如图，某部队在灯塔A的周围进行爆破作业，A的周围3千米内的水域为危险区域，有一渔船误入离A２千米的B处，为了尽快驶离危险区域，该船应沿哪条射线方向航行？（要求给予证明）
八、（本题满分12分）
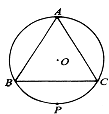37．如图，等边△ABC的面积为S ，⊙O是它的外接圆，点P是弧BC的中点.（1）试判断过点C所作⊙O的切线与直线AB是否相交，并证明你的结论.（2）设直线CP与AB相交于点D，过点B作BE⊥CD，垂足为E，证明BE是⊙O的切线，并求△BDE的面积.
九、（本题满分10分）
38．两列火车分别行驶在两平行的轨道上，其中快车车长100米，慢车车长150米，当两车相向而行时，快车驶过慢车某个窗口（快车车头到达窗口某一点至车尾离开这一点）所用的时间为5秒.（1）求两车的速度之和及两车相向而行时慢车驶过快车某个窗口（慢车车头到达窗口某一点至车尾离开这一点）所用的时间；（2）如果两车同向而行，慢车的速度不小于8米/秒，快车从后面追赶慢车，那么从快车的车头赶上慢车的车尾开始到快车的车尾离开慢车的车头所需时间至少为多少秒？
中考数学模拟试题（4）答案
一、选择题
1．D 2．A 3．B 4．B
5．D 6．D 7．C 8．D
9．B 10．B 11．A 12．B
13．C 14．C 15．D 16．B
17．C 18．C
二、填空题
19．
20．2
21．
22．
23．6π
24．
25．（0，－3）
三、
26．作法：①作直线
垂足为C； ②分别截取CB = a，CA = b； ③连结AB，则△ABC为所求作的三角形；（2）正确作出CD得1分，正确作出⊙O得2分.
四、
27．
28．在Rt△ABC中，
BC =
=
=5，
。
作
，垂足是E，BE
=
=
=
29．设正方形外接圆、内切圆的半径分别为R、r，面积为S1，S2. S =
（2分）=π
.
30设平均每月增长的百分率为x，根据题意，得
x1=0.1=10%，x 2=－2.1（不合题意，舍去）
五、
31．去分母，得
整理后，得
（5分）解这个方程，得
检验：把x = －2代入
它不等于0，所以x=－2是原方程的根；把x=1代入它等于0，所以x=1是增根. 
原方程的根是x=－2.
六、
32．连结BC， 
是⊙O的直径， 
又
△DAE∽△BAC 
七、
33．设所求函数的解析式为
把（―1，―5），（0，－4），（1，1）分别代入，得
， 解这个方程组，得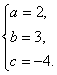
所求的函数的解析式为
34．延长PO交⊙O于点D.由割线定理，得
35．设
、
为所给方程的两根.由
得
当
，方程为
△
＞0，方程有两实根，当
时，方程为
△
＜0，方程无实根，故应舍去.故a的值为
.
36．该船应沿射线AB方向驶离危险区域证明如下：如图，设射线AB与⊙A相交于点C.在⊙A上任取一点D（不包括C关于A的对称点），连结AD、BD.在△ABD中，AB＋BD＞AD. 
＞
＞
八、
37．（1）CF是⊙O的切线CF与直线AB不相交. 证明如下： CF是⊙O的切线，△ABC是等边三角形， 
CF∥AB. CF与直线AB不相交；
（2）连结BO并延长交AC于H. 
⊙O是等边△ABC的外接圆， 
点P是BC的中点，
.又
， 
， 
BE是⊙O的切线.在△ACD中，
S△BDE = S△BCE.在矩形BHCE中， S△BCE =S△BCH =
S△BCE
S△BDE
九、
38．设快、慢车的速度分别为x 米/秒，y米/秒.根据题意，得
即两车的速度之和为20米/秒.设慢车驶过快车某个窗口需用
秒，根据题意，得
即两车相向而行时，慢车驶过快车某个窗口所用时间为7.5秒.（2）所求的时间
依题意，当慢车的速度为8米/秒时，
的值最小. 
∴t2的最小值为62.5秒.即从快车的车头赶上慢车的车尾开始到快车的车尾离开慢车的车头所需时间至少为62.5秒.