中考数学模拟试题（5）
一、选择题：（每小题3分，共15分）
1、如果0.06005是由四舍五入法得到的近似数，则它有（ ）个有效数字.
A、6 B、5 C、4 D、3
2、下列运算，错误的是（ ）.
A、
B、
C、
D、61200 = 6.12×10 4
3、矩形ABCD中，AB=3，BC=4，以AB为轴旋转一周得到圆柱，则它的表面积是（ ）.
A、56
B、32 C、24 D、60
4、已知反比例函数
的图象在一、三象限，则直线
的图象经过（ ）.
A、一、二、三象限 B、二、三、四象限
C、一、三、四象限 D、一、二、四象限
5、下列命题中，不正确的是（ ）.
A、一组邻边相等的矩形是正方形
B、等腰梯形的对角线相等
C、直角三角形斜边上的高等于斜边的一半
D、圆既是轴对称图形，又是中心对称图形
二、填空题：（每小题4分，共20分）
6、函数
中，自变量的取值范围是________________.
7、方程组
的解是
.
8、不等式
的解集是____________.
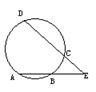
9、如图，已知A、B、C、D为圆上四点，弧AD、弧BC的度数分别为120°和40°，则∠E＝
.
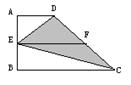
10、如图，在直角梯形ABCD中，AB⊥BC，AD∥BC，EF为中位线，
若AB＝2b，EF＝a，则阴影部分的面积 .
三、解答题：（每小题6分，共30分）
11、先化简，再求值：
， 其中
.
12、尺规作图.试将已知圆的面积四等分.
（保留作图痕迹，不写作法）
13、小强老师为了今年的升中考试，他先用120元买
了若干本数学复习资料，后来又用240元买同样的数学复
习资料：这次比上次多20本，而且店家给予优惠，每本降价4元.请问第一次他买了多少本复习资料？
14、如图，已知二次函数y＝ax
＋bx+c的图象与x轴交于点A、B，与y轴交于点C.
（1）写出A、B、C三点的坐标；（2）求出二次函数的解析式.
15、我们知道，只有两边和一角对应相等的两个三角形不一定全等.你如何处理和安排这三个条件，使这两个三角形全等.请你仿照方案（1），写出方案（2）、（3）.
解：设有两边和一角对应相等的两个三角形.
方案（1）：若这角恰好是直角，则这两个三角形全等.
方案（2）： .
方案（3）： .
四、解答题：（每小题7分，共28分）
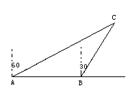16、如图，一艘渔船正以30海里/小时的速度由西向东追赶鱼群，在A处看见小岛C在船的北偏东60°.40分钟后，渔船行至B处，此时看见小岛C在船的北偏东30°.已知小岛C为中心10海里以内为我军导弹部队军事演习的着弹危险区.问这艘渔船继续向东追赶鱼群，是否有进入危险区域的可能？
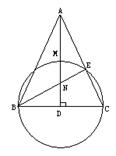17、如图，弦BC经过圆心D，AD⊥BC，AC交⊙D于E，AD交 ⊙D于M，BE交AD于N.求证：△BND∽△ABD.
18、已知关于x的一元二次方程x 2＋（2k－1）x＋k 2+1＝0.如果方程的两根之和等于两根之积，求k的值.
19、在全国初中数学联赛中，将参赛两个班学生的
成绩（得分均为整数）进行整理后分成五组，绘制出
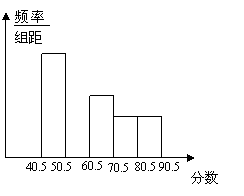如下的频率分布直方图（如图所示），已知图中从左到
右的第一、第三、第四、第五小组的频率分别是0.25、
0.15、0.10、0.10，第二组的频数是40.
（1）第二小组的频率是 ，并补全这个
频率分布直方图；
（2）这两个班参赛的学生人数是 ；
（3）这两个班参赛学生的成绩的众数落在第
组内.（不必说明理由）
五、解答题：（每小题9分，共27分）
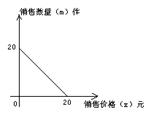20、某商场以每件10元的价格购进一种商品，试销中发现，这种商品每天的销售量m（件）与每件的销售价x（元）满足一次函数，其函数图像如图所示.
（1）求商场每天销售这种商品的销售利润y（元）与每件的销售价x（元）之间的函数解析式；
（2）试判断，每件商品的销售价格在什么范围内，每天的销售利润随着价格的提高而增加.
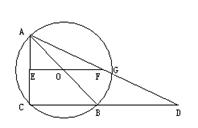21、如图，已知AB是⊙O的直径，C是⊙O上的点，连结AC、CB，过O作EO∥CB并延长EO到F，使EO＝FO，连结AF并延长AF与CB的延长线交于D.
求证：AE2＝FG·FD.
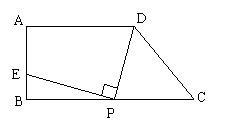
22、如图：梯形ABCD中，AD∥BC，∠ABC=90°，AD=9，BC=12，AB=6，在线段BC上任取一点P，连接DP，作射线PE⊥DP，PE与直线AB交于点E.（1）试确定当CP=3时，点E的位置；（2）若设CP=x，BE=y，试写出y关于自变量x的函数关系式.
中考模拟考试试题解答及评分说明
一、CBAAC
二、6.x＞5 7.
8. x＞5 9.40°10.ab
11.解：原式＝
（3分）＝
（6分）
12.作出第一条直径占3分，第二条直径占2分，答占1分，共6分.
13.解：设第一次买了x本，（1分）则：
（3分）
∴x＝10 或x＝－60（舍去）（5分）
答：（略）（6分）
14.解：（1）A、B、C三点的坐标为A（－1，0），B(4，0)，C(0，－3) （2分）
（2）设解析式为：y＝a（x＋1）（x－4）（3分）
∴－3＝a（0＋1）（0－4） a＝
（5分）
∴y＝
（6分）
15.方案（2）：该角恰为两边的夹角时；（3分）
方案（3）：该角为钝角时.（6分）
16.解：过点C作AB的垂线，交AB的延长线于点D，则△ADC为直角三角形（1分）
在Rt△ADC中，设CD＝x（2分）
∵AB＝30×
＝20，BD＝
＝
x（3分）
在Rt△ACD中，
（5分） ∴x＝10
＞10 （6分）
∴没有进入危险区域的可能.（7分）
17.证明：∵△ABD≌△ACD （2分） ∴∠ABD＝∠ACD（3分）
∵BC是直径，∴∠BEC＝90°
∵∠BND＝∠ANE＝90°－∠DAC＝∠ACD（5分）
∴△ABD∽△ACD（7分）
18.解：∵x
（2分）∴－2k＋1＝k＋1（4分）
∴k
＝0，k
＝－2（5分）
当k＝0时，△＝－3＜0，当k＝－2时，△＝5＞0，∴k＝－2（7分）
19.解:(1)0.4(2分)补全直方图（4分）（2）100（6分）（3）二（7分）
20.解：（1）由图像，求得一次函数的解析式为：m＝－x＋20（3分）
每件商品的利润为x－10，所以每天的利润为：
y＝（x－10）（－x＋20）（5分）
∴函数解析式为y＝－x＋30x－200（6分）
（2）∵x＝－
＝15（元）
在0＜x＜15元时，每天的销售利润随着x的增大而增大.（9分）
21.证明：连结BF、BG.（1分）
∵△AEO≌△BFO ∴AE＝BF（3分）
又∵∠ACB＝90° EG∥BC
∴∠OFB＝∠AEO＝∠ACB＝90°
∴∠FBD＝90°（6分）
又∵BG⊥FD
由△FGB∽△FBD（8分）
AE
（9分）
22.（1）解：连接DP ∵CP=3 ∴BP=BC—CP=12 —3=9 ∵AD=9 ∴AD=DP（1分）
∵AD∥DP ∴四边形ABPD是矩形 ∴ DP⊥BP （2分）
∵PE⊥DP ∴点E与点B重合 （3分）
（2）过点D作DF⊥BC，垂足为F，∴AD=BF=9 AB=DF=6
当点P在BF上：
∵∠BPE +∠EPD+∠DPF=180° PE⊥DP ∴∠BPE +∠DPF=90°（4分）
∵DF⊥BC ∴∠PDF+∠DPF=90° ∴∠PDF =∠EPB
∴∴△PEB∽△DPF ∴
（5分）
∵CP=x BE=y ∴BP=12—x PF=PC—CF=x—3
∴
（6分） ∴
（7分）
当点P在CF上，同理可求得：
（9分）
AE＝FG
∴AE＝FG