08届高考数学综合训练(六)
1、已知函数![]() ,则
,则![]() =
。2008!
=
。2008!
 2、如图,是函数
2、如图,是函数![]() 的导函数
的导函数![]() 的图象,则下面判断正确的是 C
的图象,则下面判断正确的是 C
A.在区间(-2,1)上![]() 是增函数;B.在(1,3)上
是增函数;B.在(1,3)上![]() 是减函数;
是减函数;
C.在(4,5)上![]() 是增函数;D.当
是增函数;D.当![]() 时,
时,![]() 取极大值.
取极大值.
3、已知![]() ,正实数
,正实数![]() 满足
满足![]() ,则
,则![]() 的最小值为 D
的最小值为 D
A.4 B.2
C.
![]() D.
D. ![]()
4、已知函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,则
,则![]() 的取值范围是 D
的取值范围是 D
A.![]() B.
B.![]()
C.![]() D.
D.![]()
| 4 | ||||||||
| 9 | A | 3 | 5 | 7 | ||||
| 2 | 6 | 3 | 5 | |||||
| 4 | 2 | 8 | 6 | 9 | ||||
| 1 | 7 | |||||||
| 6 | 9 | 3 | 5 | 4 | ||||
| 2 | 8 | 9 | B | 5 | ||||
| 1 | 2 | 8 | 7 | 6 | ||||
| 4 |
5、设![]() ,
,![]() ,计算
,计算![]() ________,
________,![]() ________,并由此概括出关于函数
________,并由此概括出关于函数![]() 和
和![]() 的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是_______________
的一个等式,使上面的两个等式是你写出的等式的特例,这个等式是_______________
0,0 ,![]()
6、近几年来,在欧美等国家流行一种“数独”推理游戏,游戏规则如下:
①在9×9的九宫格子中,分成9个3×3的小九宫格,用1到9这9个数字填满整个格子;
②每一行与每一列都有1到9的数字,每个小九宫格里也有1到9的数字,并且一个数字在每行、每列及每个小九宫格里只能出现一次,既不能重复也不能少.
那么A处应填入的数字为__________;B处应填入的数字为__ _.
1,3
7、已知等差数列{an}的前n项和为Sn,若M、N、P三点共线,O为坐标原点,且![]() (直线MP不过点O),则S32等于 ( B )
(直线MP不过点O),则S32等于 ( B )
8、函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ],则
],则![]() 的最大值和最小值之和为B
的最大值和最小值之和为B
A.![]() B.2
B.2![]() C.
C.![]() D.
D.![]()
9、对于各数互不相等的正数数组![]() (
(![]() 是不小于
是不小于![]() 的正整数),如果在
的正整数),如果在![]() 时有
时有![]() ,则称
,则称![]() 与
与![]() 是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组
是该数组的一个“逆序”,一个数组中所有“逆序”的个数称为此数组的“逆序数”.若各数互不相等的正数数组![]() 的“逆序数”是2,则
的“逆序数”是2,则![]() 的“逆序数”是 .
13
的“逆序数”是 .
13
10、已知函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,则
,则![]() 的最小值等于 ( B )
的最小值等于 ( B )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
 11、若函数
11、若函数![]()
![]() 且
且![]() ,图象恒过定点A,又点A在直线
,图象恒过定点A,又点A在直线![]() 上,若
上,若![]() 是正数,则
是正数,则![]() 的最小值是
.
的最小值是
.![]()
要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪都能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面,则需安装这种喷水龙头的个数最少是 ( B)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
将函数![]() 在区间
在区间![]() 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求证:
,求证:![]() ,
,![]() .
.
解:(Ⅰ)∵![]()
![]()
∴![]() 的极值点为
的极值点为![]() ,从而它在区间
,从而它在区间![]() 内的全部极值点按从小到大排列构成以
内的全部极值点按从小到大排列构成以![]() 为首项,
为首项,![]() 为公差的等差数列,
为公差的等差数列,
∴![]() ,
,![]()
(Ⅱ)由![]() 知对任意正整数
知对任意正整数![]() ,
,![]() 都不是
都不是![]() 的整数倍,
的整数倍,
所以![]() ,从而
,从而![]()
于是![]()
又![]() ,
,
![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列。 ∴
为公比的等比数列。 ∴![]() ,
,![]()
已知函数![]() (
(![]() 为常数且
为常数且![]() )
)
(1)当![]() 时,求
时,求![]() 的单调区间
的单调区间
(2)若![]() 在
在![]() 处取得极值,且
处取得极值,且![]() ,而
,而![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围(其中
的取值范围(其中![]() 为自然对数的底数)
为自然对数的底数)
解:(1)由![]() 得
得![]() ……………………(1分)
……………………(1分)
![]()
![]()
又![]() 的定义域为
的定义域为![]() ,所以
,所以![]()
当![]() 时,
时,![]()
![]()
![]()
当![]() 时,
时,![]() ,
,![]() 为减函数
为减函数
当![]() 时,
时,![]() ,
,![]() 为增函数………………………(5分)
为增函数………………………(5分)
所以当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]()
单调递减区间为![]() …………………(6分)
…………………(6分)
(2)由(1)知当![]() 时,
时,![]()
![]() ,
,![]() 递增无极值………(7分)
递增无极值………(7分)
所以![]() 在
在![]() 处有极值,故
处有极值,故![]() 且
且![]()
因为![]() 且
且![]() ,所以
,所以![]() 在
在![]() 上单调
上单调
当![]() 为增区间时,
为增区间时,![]() 恒成立,则有
恒成立,则有
 ………………………………………(9分)
………………………………………(9分)
当![]() 为减区间时,
为减区间时,![]() 恒成立,则有
恒成立,则有
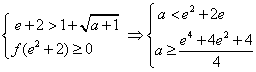 无解 ……………………(13分)
无解 ……………………(13分)
由上讨论得实数![]() 的取值范围为
的取值范围为![]() …………………………(14分)
…………………………(14分)
已知![]() 是定义在R上的函数,它在
是定义在R上的函数,它在![]() 和
和![]() 上有相同的单调性,在
上有相同的单调性,在![]() 和
和![]() 上有相反的单调性.
上有相反的单调性.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)在函数![]() 的图象上是否存在点
的图象上是否存在点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() ?若存在,求出
?若存在,求出![]() 点的坐标,若不存在,则说明理由;
点的坐标,若不存在,则说明理由;
(Ⅲ)设![]() 的图象交
的图象交![]() 轴于
轴于![]() 三点,且
三点,且![]() 的坐标为
的坐标为![]() ,求线段
,求线段![]() 的长度
的长度![]() 的取值范围.
的取值范围.
解:(Ⅰ)由题意可知![]() 在[-1,0]和[0,2]上有相反的单调性,所以
在[-1,0]和[0,2]上有相反的单调性,所以![]() 是
是![]() 的一个极值点.
的一个极值点.
故![]() ,即
,即![]() 是
是![]() 的一个解,所以
的一个解,所以![]() .
.
(Ⅱ)因为![]() 在
在 ![]() 和
和![]() 上有相反的单调性,所以
上有相反的单调性,所以![]() 在
在![]() 上必有一根.又
上必有一根.又![]() ,易知方程
,易知方程![]() 一根为
一根为![]() ,另一根为
,另一根为![]() ,所以
,所以![]() ,∴
,∴![]()
假设存在点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() ,则
,则![]() ,即
,即![]() 有解.而
有解.而![]() =
=![]() ,因为
,因为![]() ,所以
,所以![]() ,与
,与![]() 有解矛盾。故不存在点
有解矛盾。故不存在点![]() ,使得
,使得![]() 在点
在点![]() 的切线斜率为
的切线斜率为![]() .
.
(Ⅲ)依题意有![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以![]() =
=![]()
=![]() =
=![]() ,
,
![]() 两点的横坐标
两点的横坐标![]() 就是方程
就是方程
![]() 的两根,所以
的两根,所以
![]() =
=![]() =
=![]() =
=![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() =
=![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.