江苏省徐州市
08届高考数学二轮复习圆锥曲线测试题
一、填空题（共14小题，每题5分，计70分）
1． 称焦距与短轴长相等的椭圆为“黄金椭圆”，则黄金椭圆的离心率为 ．
2．中心在原点，焦点在坐标轴的双曲线的一条渐近线方程为
，其离心率是
3．已知双曲线
的焦点为
、
，点
在双曲线上且
轴，则到直线
的距离为 ____________
4．抛物线
的焦点坐标为 ____________
5. 已知△ABC的顶点B、C在椭圆
上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是 ____________
6. 椭圆
的焦点
、
，
为椭圆上的一点，已知
，则△
的面积为 ____________
7．已知抛物线
，一定点A（3，1），F是抛物线的焦点，点P是抛物线上一点，
AP+PF的最小值____________。
8．正四棱锥的侧棱长和底面边长都是1，则侧棱和底面所成的角为____________。
9．以下同个关于圆锥曲线的命题中①设A、B为两个定点，k为非零常数，
，则动点P的轨迹为双曲线；②过定圆C上一定点A作圆的动点弦AB，O为坐标原点，若
则动点P的轨迹为椭圆；③方程
的两根可分别作为椭圆和双曲线的离心率；④双曲线
有相同的焦点.其中真命题的序号为 ____________。（写出所有真命题的序号）
10．方程
表示椭圆的充要条件是
．
11．在区间[1,5]和[2,4]分别各取一个数，记为m和n，则方程
表示焦点在x轴上的椭圆的概率是
．
12.嫦娥一号奔月前第一次变轨后运行轨道是以地球中心F为焦点的椭圆，测得近地点A距离地面
，远地点B距离地面
，地球半径为
，关于这个椭圆有以下四种说法：①焦距长为
；②短半轴长为
；③离心率
；其中正确的序号为______
__．
13．以椭圆
内的点
为中点的弦所在直线方程为
．
14．设
分别是双曲线
的左、右焦点．若点在双曲线上，且
，则
．
高三数学圆锥曲线测试题答题纸
班级 姓名 分数
一、填空题（共14小题，每小题5分，满分70分．）
1、 2、 3
4、 5、 6
7、 8、 9
10、 11、 12
13、 14、
二、解答题（6大题共90分，要求有必要的文字说明和步骤）
15．点A、B分别是椭圆
长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于
轴上方，
.求点P的坐标；
.
16. (1) 已知椭圆C的焦点F1（－
，0）和F2（，0），长轴长6，设直线
交椭圆C于A、B两点，求线段AB的中点坐标。
(2) 已知双曲线与椭圆
共焦点，它们的离心率之和为
，求双曲线方程.
17．已知抛物线C: y=-
x2+6, 点P（2, 4）、A、B在抛物线上, 且直线PA、PB的倾斜角互补.
(Ⅰ)证明:直线AB的斜率为定值;
(Ⅱ)当直线AB在y轴上的截距为正数时, 求△PAB面积的最大值及此时直线AB的方程.
18．双曲线
(a>1,b>0)的焦距为2c,直线l过点(a,0)和(0,b),且点(1,0)到直线l的距离与点(-1,0)到直线l的距离之和s≥
c.求双曲线的离心率e的取值范围
19．已知抛物线
的焦点为F，A是抛物线上横坐标为4、且位于轴上方的点，A到抛物线准线的距离等于5.过A作AB垂直于
轴，垂足为B，OB的中点为M.。
（1）求抛物线方程；
（2）过M作
，垂足为N，求点N的坐标；
（3）以M为圆心，MB为半径作圆M，当
是轴上一动点时，讨论直线AK与圆M的位置关系.
20.椭圆C: 
的两个焦点为F1,F2,点P在椭圆C上，且
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线
过圆x2+y2+4x-2y=0的圆心，交椭圆C于A、B两点，且A、B关于点M对称，求直线的方程.
高三数学圆锥曲线测试答案
1.
2. 
或
3.
4. 
5.
4
6. 9 7. 4 8. 
9.③④ 10.
11.
12.① ② ③ 13.
14. 
15. 解:由已知可得点A（－6，0），F（4，0）
设点P的坐标是
，由已知得
由于
16解:由已知条件得椭圆的焦点在x轴上,其中c=,a=3,从而b=1,所以其标准方程是:
.联立方程组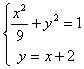
,消去y得, 
.
设A(
),B(
),AB线段中点为M(
)那么: 
,
所以
也就是说线段AB中点坐标为
（2）解:由于椭圆焦点为F(0,
4),离心率为e=
,所以双曲线的焦点为F(0,4),离心率为2,
从而c=4,a=2,b=2
.
所以求双曲线方程为: 
.
(17) (Ⅰ)证: 易知点P在抛物线C上, 设PA的斜率为k, 则直线PA的方程是y-4=k(x-2).
代入y=-x2+6并整理得x2+2kx-4(k+1)=0此时方程应有根xA及2,
由韦达定理得:
2xA=-4(k+1) , ∴xA=-2(k+1). ∴yA=k(xA-2)+4.=-k2-4k+4. ∴A(-2(k+1), -k2-4k+4).
由于PA与PB的倾斜角互补, 故PB的斜率为-k.
同理可得B(-2(-k+1), -k2+4k+4)
∴kAB=2.
(Ⅱ) ∵AB的方程为y=2x+b, b>0.代入方程y=-x2+6消去y得x2+2x+b-6=0.
AB=2
.
∴S=ABd=·2
.
此时方程为y=2x+
.
(18) 解:直线l的方程为bx+ay-ab=0.由点到直线的距离公式,且a>1,
得到点(1,0)到直线l的距离d1 =
.
同理得到点(-1,0)到直线l的距离d2 =
.
s= d1 +d2=
=
.
由s≥c,得≥c,即5a
≥2c2.
于是得5
≥2e2.即4e2-25e+25≤0.
解不等式,得
≤e2≤5.由于e>1>0,
所以e的取值范围是
(19) 解：（1）抛物线
∴抛物线方程为y2= 4x.
（2）∵点A的坐标是（4，4）， 由题意得B（0，4），M（0，2），
又∵F（1，0）， ∴
则FA的方程为y=
（x－1），MN的方程为
解方程组
（3）由题意得，圆M的圆心是点（0，2），半径为2.
当m=4时，直线AK的方程为x=4，此时，直线AK与圆M相离，
当m≠4时，直线AK的方程为
即为
圆心M（0，2）到直线AK的距离
，令
时，直线AK与圆M相离；
当m=1时，直线AK与圆M相切；
当
时，直线AK与圆M相交.
20解法一：
(Ⅰ)因为点P在椭圆C上，所以
，a=3.
在Rt△PF1F2中，
故椭圆的半焦距c=
,
从而b2=a2－c2=4,
所以椭圆C的方程为
＝1.
(Ⅱ)设A，B的坐标分别为（x1,y1）、（x2,y2）.
已知圆的方程为（x+2）2+(y－1)2=5,所以圆心M的坐标为（－2，1）.
从而可设直线l的方程为
y=k(x+2)+1,
代入椭圆C的方程得
（4+9k2）x2+(36k2+18k)x+36k2+36k－27=0.
因为A，B关于点M对称.
所以
解得
，
所以直线l的方程为
即8x-9y+25=0. (经检验，所求直线方程符合题意)
解法二：(Ⅰ)同解法一.
(Ⅱ)已知圆的方程为（x+2）2+(y－1)2=5,所以圆心M的坐标为（－2，1）.
设A，B的坐标分别为（x1,y1）,(x2,y2).由题意x1
x2且
① 
②
由①－②得 
③
因为A、B关于点M对称，
所以x1+ x2=－4, y1+ y2=2,
代入③得
＝
，
即直线l的斜率为，
所以直线l的方程为y－1＝（x+2），
即8x－9y+25=0.
(经检验，所求直线方程符合题意.)