08高考理科数学二轮复习概率与统计实效性训练(一)
一. 考点回顾:1.两个原理及排列组合的理解和应用;
2.排列数与组合数的公式与性质;
3.二项式定理的通项公式与赋值法的理解及应用;
4.等可能性事件,互斥事件(对立事件),独立事件(独立重复试验)的意义及其概率的求法;
5.(理科)离散型随机变量的分布列、数学期望与方差的求法和实际意义;
6.频率分布表及频率分布条形图、直方图的理解和应用;
7.简单随机抽样、系统抽样、分层抽样的操作方法以及它们的区别与联系;
8. (理科)正态分布与正态曲线的概念与性质的理解并掌握简单应用;
9. (理科)了解线性回归的概念及性质;
(一)、两个原理.
1. 乘法原理、加法原理.
2. 可以有重复元素的排列.
从m个不同元素中,每次取出n个元素,元素可以重复出现,按照一定的顺序排成一排,那么第一、第二……第n位上选取元素的方法都是m个,所以从m个不同元素中,每次取出n个元素可重复排列数m·m·… m = mn.. 例如:n件物品放入m个抽屉中,不限放法,共有多少种不同放法?
(解:![]() 种)
种)
(二)、排列.
1. ⑴对排列定义的理解.
定义:从n个不同的元素中任取m(m≤n)个元素,按照一定顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
⑵相同排列.
如果;两个排列相同,不仅这两个排列的元素必须完全相同,而且排列的顺序也必须完全相同.
⑶排列数.
从n个不同元素中取出m(m≤n)个元素排成一列,称为从n个不同元素中取出m个元素的一个排列. 从n个不同元素中取出m个元素的一个排列数,用符号![]() 表示.
表示.
⑷排列数公式:
![]()
注意:![]() 规定0! = 1
规定0! = 1
![]()
![]() 规定
规定![]()
2. 含有可重元素的排列问题.
对含有相同元素求排列个数的方法是:设重集S有k个不同元素a1,a2,…...an其中限重复数为n1、n2……nk,且n = n1+n2+……nk ,
则S的排列个数等于![]() .
.
例如:已知数字3、2、2,求其排列个数![]() 又例如:数字5、5、5、求其排列个数?其排列个数
又例如:数字5、5、5、求其排列个数?其排列个数![]() .
.
(三)、组合.
1. ⑴组合:从n个不同的元素中任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合.
⑵组合数公式:![]()
⑶两个公式:①![]() ②
②![]()
①从n个不同元素中取出m个元素后就剩下n-m个元素,因此从n个不同元素中取出 n-m个元素的方法是一一对应的,因此是一样多的就是说从n个不同元素中取出n-m个元素的唯一的一个组合.
(或者从n+1个编号不同的小球中,n个白球一个红球,任取m个不同小球其不同选法,分二类,一类是含红球选法有![]() 一类是不含红球的选法有
一类是不含红球的选法有![]() )
)
②根据组合定义与加法原理得;在确定n+1个不同元素中取m个元素方法时,对于某一元素,只存在取与不取两种可能,如果取这一元素,则需从剩下的n个元素中再取m-1个元素,所以有C![]() ,如果不取这一元素,则需从剩余n个元素中取出m个元素,所以共有C
,如果不取这一元素,则需从剩余n个元素中取出m个元素,所以共有C![]() 种,依分类原理有
种,依分类原理有![]() .
.
⑷排列与组合的联系与区别.
联系:都是从n个不同元素中取出m个元素.
区别:前者是“排成一排”,后者是“并成一组”,前者有顺序关系,后者无顺序关系.
(四)、排列、组合综合.
1. I. 排列、组合问题几大解题方法及题型:
①直接法. ②排除法.
③捆绑法:在特定要求的条件下,将几个相关元素当作一个元素来考虑,待整体排好之后再考虑它们“局部”的排列.它主要用于解决“元素相邻问题”,例如,一般地,n个不同元素排成一列,要求其中某![]() 个元素必相邻的排列有
个元素必相邻的排列有![]() 个.其中
个.其中![]() 是一个“整体排列”,而
是一个“整体排列”,而![]() 则是“局部排列”.
则是“局部排列”.
又例如①有n个不同座位,A、B两个不能相邻,则有排列法种数为![]()
![]() .
.
②有n件不同商品,若其中A、B排在一起有![]() .
.
③有n件不同商品,若其中有二件要排在一起有![]() .
.
注:①③区别在于①是确定的座位,有![]() 种;而③的商品地位相同,是从n件不同商品任取的2个,有不确定性.
种;而③的商品地位相同,是从n件不同商品任取的2个,有不确定性.
④插空法:先把一般元素排列好,然后把待定元素插排在它们之间或两端的空档中,此法主要解决“元素不相邻问题”.
例如:n个元素全排列,其中m个元素互不相邻,不同的排法种数为多少?![]() (插空法),当n – m+1≥m, 即m≤
(插空法),当n – m+1≥m, 即m≤![]() 时有意义.
时有意义.
⑤占位法:从元素的特殊性上讲,对问题中的特殊元素应优先排列,然后再排其他一般元素;从位置的特殊性上讲,对问题中的特殊位置应优先考虑,然后再排其他剩余位置.即采用“先特殊后一般”的解题原则.
⑥调序法:当某些元素次序一定时,可用此法.解题方法是:先将n个元素进行全排列有![]() 种,
种,![]() 个元素的全排列有
个元素的全排列有![]() 种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到去调序的作用,即若n个元素排成一列,其中m个元素次序一定,共有
种,由于要求m个元素次序一定,因此只能取其中的某一种排法,可以利用除法起到去调序的作用,即若n个元素排成一列,其中m个元素次序一定,共有![]() 种排列方法.
种排列方法.
例如:n个元素全排列,其中m个元素顺序不变,共有多少种不同的排法?
解法一:(逐步插空法)(m+1)(m+2)…n = n!/ m!;解法二:(比例分配法)![]() .
.
⑦平均法:若把kn个不同元素平均分成k组,每组n个,共有![]() .
.
例如:从1,2,3,4中任取2个元素将其平均分成2组有几种分法?有![]() (平均分组就用不着管组与组之间的顺序问题了)又例如将200名运动员平均分成两组,其中两名种子选手必在一组的概率是多少?
(平均分组就用不着管组与组之间的顺序问题了)又例如将200名运动员平均分成两组,其中两名种子选手必在一组的概率是多少?
(![]() )
)
注意:分组与插空综合. 例如:n个元素全排列,其中某m个元素互不相邻且顺序不变,共有多少种排法?有![]() ,当n – m+1 ≥m, 即m≤
,当n – m+1 ≥m, 即m≤![]() 时有意义.
时有意义.
⑧隔板法:常用于解正整数解组数的问题.
![]() 例如:
例如:![]() 的正整数解的组数就可建立组合模型将12个完全相同的球排成一列,在它们之间形成11个空隙中任选三个插入3块摸板,把球分成4个组.每一种方法所得球的数目依次为
的正整数解的组数就可建立组合模型将12个完全相同的球排成一列,在它们之间形成11个空隙中任选三个插入3块摸板,把球分成4个组.每一种方法所得球的数目依次为![]() 显然
显然![]() ,故(
,故(![]() )是方程的一组解.反之,方程的任何一组解
)是方程的一组解.反之,方程的任何一组解![]() ,对应着惟一的一种在12个球之间插入隔板的方式(如图所示)故方程的解和插板的方法一一对应. 即方程的解的组数等于插隔板的方法数
,对应着惟一的一种在12个球之间插入隔板的方式(如图所示)故方程的解和插板的方法一一对应. 即方程的解的组数等于插隔板的方法数![]() .
.
注意:若为非负数解的x个数,即用![]() 中
中![]() 等于
等于![]() ,有
,有![]() ,进而转化为求a的正整数解的个数为
,进而转化为求a的正整数解的个数为![]() .
.
⑨定位问题:从n个不同元素中每次取出k个不同元素作排列规定某r个元素都包含在内,并且都排在某r个指定位置则有![]() .
.
例如:从n个不同元素中,每次取出m个元素的排列,其中某个元素必须固定在(或不固定在)某一位置上,共有多少种排法?
固定在某一位置上:![]() ;不在某一位置上:
;不在某一位置上:![]() 或
或![]() (一类是不取出特殊元素a,有
(一类是不取出特殊元素a,有![]() ,一类是取特殊元素a,有从m-1个位置取一个位置,然后再从n-1个元素中取m-1,这与用插空法解决是一样的)
,一类是取特殊元素a,有从m-1个位置取一个位置,然后再从n-1个元素中取m-1,这与用插空法解决是一样的)
⑩指定元素排列组合问题.
i. 从n个不同元素中每次取出k个不同的元素作排列(或组合),规定某r个元素都包含在内 。先C后A策略,排列![]() ;组合
;组合![]() .
.
ii. 从n个不同元素中每次取出k个不同元素作排列(或组合),规定某r个元素都不包含在内。先C后A策略,排列![]() ;组合
;组合![]() .
.
iii 从n个不同元素中每次取出k个不同元素作排列(或组合),规定每个排列(或组合)都只包含某r个元素中的s个元素。先C后A策略,排列![]() ;组合
;组合![]() .
.
II. 排列组合常见解题策略:
①特殊元素优先安排策略;②合理分类与准确分步策略;③排列、组合混合问题先选后排的策略(处理排列组合综合性问题一般是先选元素,后排列);④正难则反,等价转化策略;⑤相邻问题插空处理策略;
⑥不相邻问题插空处理策略;⑦定序问题除法处理策略;⑧分排问题直排处理的策略;⑨“小集团”排列问题中先整体后局部的策略;⑩构造模型的策略.
2. 组合问题中分组问题和分配问题.
①均匀不编号分组:将n个不同元素分成不编号的m组,假定其中r组元素个数相等,不管是否分尽,其分法种数为![]() (其中A为非均匀不编号分组中分法数).如果再有K组均匀分组应再除以
(其中A为非均匀不编号分组中分法数).如果再有K组均匀分组应再除以![]() .
.
例:10人分成三组,各组元素个数为2、4、4,其分法种数为![]() .若分成六组,各组人数分别为1、1、2、2、2、2,其分法种数为
.若分成六组,各组人数分别为1、1、2、2、2、2,其分法种数为![]()
②非均匀编号分组: n个不同元素分组,各组元素数目均不相等,且考虑各组间的顺序,其分法种数为![]()
例:10人分成三组,各组人数分别为2、3、5,去参加不同的劳动,其安排方法为:![]() 种.
种.
若从10人中选9人分成三组,人数分别为2、3、4,参加不同的劳动,则安排方法有![]() 种
种
③均匀编号分组:n个不同元素分成m组,其中r组元素个数相同且考虑各组间的顺序,其分法种数为![]() .
.
例:10人分成三组,人数分别为2、4、4,参加三种不同劳动,分法种数为![]()
④非均匀不编号分组:将n个不同元素分成不编号的m组,每组元素数目均不相同,且不考虑各组间顺序,不管是否分尽,其分法种数为![]()
![]() …
…![]()
例:10人分成三组,每组人数分别为2、3、5,其分法种数为![]() 若从10人中选出6人分成三组,各组人数分别为1、2、3,其分法种数为
若从10人中选出6人分成三组,各组人数分别为1、2、3,其分法种数为![]() .
.
(五)、二项式定理.
1. ⑴二项式定理:![]() .
.
展开式具有以下特点:
① 项数:共有![]() 项;
项;
② 系数:依次为组合数![]()
③ 每一项的次数是一样的,即为n次,展开式依a的降幕排列,b的升幕排列展开.
⑵二项展开式的通项.
![]() 展开式中的第
展开式中的第![]() 项为:
项为:![]() .
.
⑶二项式系数的性质.
①在二项展开式中与首未两项“等距离”的两项的二项式系数相等;
②二项展开式的中间项二项式系数最大.
I.
当n是偶数时,中间项是第![]() 项,它的二项式系数
项,它的二项式系数![]() 最大;
最大;
II.
当n是奇数时,中间项为两项,即第![]() 项和第
项和第![]() 项,它们的二项式系数
项,它们的二项式系数![]() 最大.
最大.
③系数和:
![]()
附:一般来说![]() 为常数)在求系数最大的项或最小的项时均可直接根据性质二求解. 当
为常数)在求系数最大的项或最小的项时均可直接根据性质二求解. 当![]() 时,一般采用解不等式组
时,一般采用解不等式组![]() 的系数或系数的绝对值)的办法来求解.
的系数或系数的绝对值)的办法来求解.
⑷如何来求![]() 展开式中含
展开式中含![]() 的系数呢?其中
的系数呢?其中![]() 且
且![]() 把
把![]() 视为二项式,先找出含有
视为二项式,先找出含有![]() 的项
的项![]() ,另一方面在
,另一方面在![]() 中含有
中含有![]() 的项为
的项为![]() ,故在
,故在![]() 中含
中含![]() 的项为
的项为![]() .其系数为
.其系数为![]() .
.
(六)、概率.
1. 概率:随机事件A的概率是频率的稳定值,反之,频率是概率的近似值.
2. 等可能事件的概率:如果一次试验中可能出现的结果有年n个,且所有结果出现的可能性都相等,那么,每一个基本事件的概率都是![]() ,如果某个事件A包含的结果有m个,那么事件A的概率
,如果某个事件A包含的结果有m个,那么事件A的概率![]() .
.
3. ①互斥事件:不可能同时发生的两个事件叫互斥事件. 如果事件A、B互斥,那么事件A+B发生(即A、B中有一个发生)的概率,等于事件A、B分别发生的概率和,即P(A+B)=P(A)+P(B),推广:![]() .
.
 ②对立事件:两个事件必有一个发生的互斥事件叫对立事件. 例如:从1~52张扑克牌中任取一张抽到“红桃”与抽到“黑桃”互为互斥事件,因为其中一个不可能同时发生,但又不能保证其中一个必然发生,故不是对立事件.而抽到“红色牌”与抽到黑色牌“互为对立事件,因为其中一个必发生.
②对立事件:两个事件必有一个发生的互斥事件叫对立事件. 例如:从1~52张扑克牌中任取一张抽到“红桃”与抽到“黑桃”互为互斥事件,因为其中一个不可能同时发生,但又不能保证其中一个必然发生,故不是对立事件.而抽到“红色牌”与抽到黑色牌“互为对立事件,因为其中一个必发生.
注意:i.对立事件的概率和等于1:![]() .
.
ii.互为对立的两个事件一定互斥,但互斥不一定是对立事件.
③相互独立事件:事件A(或B)是否发生对事件B(或A)发生的概率没有影响.这样的两个事件叫做相互独立事件. 如果两个相互独立事件同时发生的概率,等于每个事件发生的概率的积,即P(A·B)=P(A)·P(B). 由此,当两个事件同时发生的概率P(AB)等于这两个事件发生概率之和,这时我们也可称这两个事件为独立事件.例如:从一副扑克牌(52张)中任抽一张设A:“抽到老K”;B:“抽到红牌”则 A应与B互为独立事件[看上去A与B有关系很有可能不是独立事件,但![]() .又事件AB表示“既抽到老K对抽到红牌”即“抽到红桃老K或方块老K”有
.又事件AB表示“既抽到老K对抽到红牌”即“抽到红桃老K或方块老K”有![]() ,因此有
,因此有![]() .
.
推广:若事件![]() 相互独立,则
相互独立,则![]() .
.
注意:i. 一般地,如果事件A与B相互独立,那么A 与![]() 与B,
与B,![]() 与
与![]() 也都相互独立.
也都相互独立.
ii. 必然事件与任何事件都是相互独立的.
iii. 独立事件是对任意多个事件来讲,而互斥事件是对同一实验来讲的多个事件,且这多个事件不能同时发生,故这些事件相互之间必然影响,因此互斥事件一定不是独立事件.
④独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的. 如果在一次试验中某事件发生的概率为P,那么在n次独立重复试验中这个事件恰好发生k次的概率:![]() .
.
4. 对任何两个事件都有![]()
(七)、随机变量.
1. 随机试验的结构应该是不确定的.试验如果满足下述条件:
①试验可以在相同的情形下重复进行;②试验的所有可能结果是明确可知的,并且不止一个;③每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果.
它就被称为一个随机试验.
2. 离散型随机变量:如果对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.若ξ是一个随机变量,a,b是常数.则![]() 也是一个随机变量.一般地,若ξ是随机变量,
也是一个随机变量.一般地,若ξ是随机变量,![]() 是连续函数或单调函数,则
是连续函数或单调函数,则![]() 也是随机变量.也就是说,随机变量的某些函数也是随机变量.
也是随机变量.也就是说,随机变量的某些函数也是随机变量.
设离散型随机变量ξ可能取的值为:![]()
ξ取每一个值![]() 的概率
的概率![]() ,则表称为随机变量ξ的概率分布,简称ξ的分布列.
,则表称为随机变量ξ的概率分布,简称ξ的分布列.
|
|
|
| … |
| … |
| P |
|
| … |
| … |
有性质①![]() ;
②
;
②![]() .
.
注意:若随机变量可以取某一区间内的一切值,这样的变量叫做连续型随机变量.例如:![]() 即
即![]() 可以取0~5之间的一切数,包括整数、小数、无理数.
可以取0~5之间的一切数,包括整数、小数、无理数.
3. ⑴二项分布:如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率是:![]() [其中
[其中![]() ]
]
于是得到随机变量ξ的概率分布如下:我们称这样的随机变量ξ服从二项分布,记作![]() ~B(n·p),其中n,p为参数,并记
~B(n·p),其中n,p为参数,并记![]() .
.
⑵二项分布的判断与应用.
①二项分布,实际是对n次独立重复试验.关键是看某一事件是否是进行n次独立重复,且每次试验只有两种结果,如果不满足此两条件,随机变量就不服从二项分布.
②当随机变量的总体很大且抽取的样本容量相对于总体来说又比较小,而每次抽取时又只有两种试验结果,此时可以把它看作独立重复试验,利用二项分布求其分布列.
4. 几何分布:“![]() ”表示在第k次独立重复试验时,事件第一次发生,如果把k次试验时事件A发生记为
”表示在第k次独立重复试验时,事件第一次发生,如果把k次试验时事件A发生记为![]() ,事A不发生记为
,事A不发生记为![]() ,那么
,那么![]() .根据相互独立事件的概率乘法分式:
.根据相互独立事件的概率乘法分式:![]()
![]() 于是得到随机变量ξ的概率分布列.
于是得到随机变量ξ的概率分布列.
|
| 1 | 2 | 3 | … | k | … |
| P | q | qp |
| … |
| … |
我们称ξ服从几何分布,并记![]() ,其中
,其中![]()
5. ⑴超几何分布:一批产品共有N件,其中有M(M<N)件次品,今抽取![]() 件,则其中的次品数ξ是一离散型随机变量,分布列为
件,则其中的次品数ξ是一离散型随机变量,分布列为![]() .〔分子是从M件次品中取k件,从N-M件正品中取n-k件的取法数,如果规定
.〔分子是从M件次品中取k件,从N-M件正品中取n-k件的取法数,如果规定![]() <
<![]() 时
时![]() ,则k的范围可以写为k=0,1,…,n.〕
,则k的范围可以写为k=0,1,…,n.〕
⑵超几何分布的另一种形式:一批产品由 a件次品、b件正品组成,今抽取n件(1≤n≤a+b),则次品数ξ的分布列为![]() .
.
⑶超几何分布与二项分布的关系.
设一批产品由a件次品、b件正品组成,不放回抽取n件时,其中次品数ξ服从超几何分布.若放回式抽取,则其中次品数![]() 的分布列可如下求得:把
的分布列可如下求得:把![]() 个产品编号,则抽取n次共有
个产品编号,则抽取n次共有![]() 个可能结果,等可能:
个可能结果,等可能:![]() 含
含![]() 个结果,故
个结果,故![]() ,即
,即![]() ~
~![]() .[我们先为k个次品选定位置,共
.[我们先为k个次品选定位置,共![]() 种选法;然后每个次品位置有a种选法,每个正品位置有b种选法] 可以证明:当产品总数很大而抽取个数不多时,
种选法;然后每个次品位置有a种选法,每个正品位置有b种选法] 可以证明:当产品总数很大而抽取个数不多时,![]() ,因此二项分布可作为超几何分布的近似,无放回抽样可近似看作放回抽样.
,因此二项分布可作为超几何分布的近似,无放回抽样可近似看作放回抽样.
(八)、数学期望与方差.
1. 期望的含义:一般地,若离散型随机变量ξ的概率分布为
|
|
|
| … |
| … |
| P |
|
| … |
| … |
则称![]() 为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
为ξ的数学期望或平均数、均值.数学期望又简称期望.数学期望反映了离散型随机变量取值的平均水平.
2. ⑴随机变量![]() 的数学期望:
的数学期望:![]()
①当![]() 时,
时,![]() ,即常数的数学期望就是这个常数本身.
,即常数的数学期望就是这个常数本身.
②当![]() 时,
时,![]() ,即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.
,即随机变量ξ与常数之和的期望等于ξ的期望与这个常数的和.
③当![]() 时,
时,![]() ,即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.
,即常数与随机变量乘积的期望等于这个常数与随机变量期望的乘积.
| ξ | 0 | 1 |
| P | q | p |
⑵单点分布:![]() 其分布列为:
其分布列为:![]() .
.
⑶两点分布:![]() ,其分布列为:(p + q = 1)
,其分布列为:(p + q = 1)
⑷二项分布:![]() 其分布列为
其分布列为![]() ~
~![]() .(P为发生
.(P为发生![]() 的概率)
的概率)
⑸几何分布:![]() 其分布列为
其分布列为![]() ~
~![]() .(P为发生
.(P为发生![]() 的概率)
的概率)
3.方差、标准差的定义:当已知随机变量ξ的分布列为![]() 时,则称
时,则称![]() 为ξ的方差. 显然
为ξ的方差. 显然![]() ,故
,故![]() 为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.
为ξ的根方差或标准差.随机变量ξ的方差与标准差都反映了随机变量ξ取值的稳定与波动,集中与离散的程度.![]() 越小,稳定性越高,波动越小.
越小,稳定性越高,波动越小.
4.方差的性质.
⑴随机变量![]() 的方差
的方差![]() .(a、b均为常数)
.(a、b均为常数)
| ξ | 0 | 1 |
| P | q | p |
⑵单点分布:![]() 其分布列为
其分布列为![]()
⑶两点分布:![]() 其分布列为:(p + q = 1)
其分布列为:(p + q = 1)
⑷二项分布:![]()
⑸几何分布:![]()
5. 期望与方差的关系.
⑴如果![]() 和
和![]() 都存在,则
都存在,则![]()
⑵设ξ和![]() 是互相独立的两个随机变量,则
是互相独立的两个随机变量,则![]()
⑶期望与方差的转化:![]() ⑷
⑷![]() (因为
(因为![]() 为一常数)
为一常数)![]() .
.
四、正态分布.(基本不列入考试范围)
1.密度曲线与密度函数:对于连续型随机变量ξ,位于x轴上方,ξ落在任一区间![]() 内的概率等于它与x轴.直线
内的概率等于它与x轴.直线![]() 与直线
与直线![]() 所围成的曲边梯形的面积
所围成的曲边梯形的面积
 (如图阴影部分)的曲线叫ξ的密度曲线,以其作为
(如图阴影部分)的曲线叫ξ的密度曲线,以其作为
图像的函数![]() 叫做ξ的密度函数,由于“
叫做ξ的密度函数,由于“![]() ”
”
是必然事件,故密度曲线与x轴所夹部分面积等于1.
2. ⑴正态分布与正态曲线:如果随机变量ξ的概率密度为:![]() . (
. (![]() 为常数,且
为常数,且![]() ),称ξ服从参数为
),称ξ服从参数为![]() 的正态分布,用
的正态分布,用![]() ~
~![]() 表示.
表示.![]() 的表达式可简记为
的表达式可简记为![]() ,它的密度曲线简称为正态曲线.
,它的密度曲线简称为正态曲线.
⑵正态分布的期望与方差:若![]() ~
~![]() ,则ξ的期望与方差分别为:
,则ξ的期望与方差分别为:![]() .
.
⑶正态曲线的性质.
①曲线在x轴上方,与x轴不相交.
②曲线关于直线![]() 对称.
对称.
③当![]() 时曲线处于最高点,当x向左、向右远离时,曲线不断地降低,呈现出“中间高、两边低”的钟形曲线.
时曲线处于最高点,当x向左、向右远离时,曲线不断地降低,呈现出“中间高、两边低”的钟形曲线.
④当![]() <
<![]() 时,曲线上升;当
时,曲线上升;当![]() >
>![]() 时,曲线下降,并且当曲线向左、向右两边无限延伸时,以x轴为渐近线,向x轴无限的靠近.
时,曲线下降,并且当曲线向左、向右两边无限延伸时,以x轴为渐近线,向x轴无限的靠近.
⑤当![]() 一定时,曲线的形状由
一定时,曲线的形状由![]() 确定,
确定,![]() 越大,曲线越“矮胖”.表示总体的分布越分散;
越大,曲线越“矮胖”.表示总体的分布越分散;![]() 越小,曲线越“瘦高”,表示总体的分布越集中.
越小,曲线越“瘦高”,表示总体的分布越集中.
3. ⑴标准正态分布:如果随机变量ξ的概率函数为![]() ,则称ξ服从标准正态分布. 即
,则称ξ服从标准正态分布. 即![]() ~
~![]() 有
有![]() ,
,![]() 求出,而P(a<
求出,而P(a<![]() ≤b)的计算则是
≤b)的计算则是![]() .
.
 注意:当标准正态分布的
注意:当标准正态分布的![]() 的X取0时,有
的X取0时,有![]() 当
当![]() 的X取大于0的数时,有
的X取大于0的数时,有![]() .比如
.比如![]() 则
则![]() 必然小于0,如图.
必然小于0,如图.
⑵正态分布与标准正态分布间的关系:若![]() ~
~![]() 则ξ的分布函数通
则ξ的分布函数通
常用![]() 表示,且有
表示,且有![]() .
.
二.高考命题预测与分析:考查一至二道客观题(5-10分)和一道解答题(12分)难度为中低档题
三.考点针对性训练:
客观题部分:
(一). 两个原理及排列组合的理解和应用;
1.(全国Ⅰ卷文科第5题)甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有( C )
A.36种 B.48种 C.96种 D.192种
2.(全国Ⅱ卷理科第10题)从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动,每人一天,要求星期五有2人参加,星期六、星期日各有1人参加,则不同的选派方法共有( B )
A.40种 B.60种 C.100种 D.120种
3.(全国Ⅱ卷文科第10题)5位同学报名参加两个课外活动小组,每位同学限报其中的一个小组,则不同的报名方法共有( D )
A.10种 B.20种 C.25种 D.32种
4.(北京理科第5题)记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( B )
A.1440种 B.960种 C.720种 D.480种
5.(北京文科第5题)某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有( A )
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
6.(四川理科第10题)用数字0,1,2,3,4,5可以组成没有重复数字,并且比20000大的五位偶数共有( B )
(A)288个 (B)240个 (C)144个 (D)126个
7.(福建文科第12题)某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“![]() ”到“
”到“![]() ”共
”共![]() 个号码.公司规定:凡卡号的后四位带有数字“
个号码.公司规定:凡卡号的后四位带有数字“![]() ”或“
”或“![]() ”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( C )
”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 8.(广东理科第7题、文科第10题)图3是某汽车维修公司的维修点环形分布图.公司在年初分配给A、 B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D 四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(
8.(广东理科第7题、文科第10题)图3是某汽车维修公司的维修点环形分布图.公司在年初分配给A、 B、C、D四个维修点某种配件各50件.在使用前发现需将A、B、C、D 四个维修点的这批配件分别调整为40、45、54、61件,但调整只能在相邻维修点之间进行.那么要完成上述调整,最少的调动件次(![]() 件配件从一个维修点调整到相邻维修点的调动件次为
件配件从一个维修点调整到相邻维修点的调动件次为![]() )为( C )
)为( C )
A.18 B.17 C.16 D.15
9.(辽宁文科地第12题)将数字1,2,3,4,5,6拼成一列,记第![]() 个数为
个数为![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则不同的排列方法种数为( B )
,则不同的排列方法种数为( B )
A.18 B.30 C.36 D.48
10.(全国Ⅰ卷理科第13题)从班委会5名成员中选出3名,分别担任班级学习委员、文娱委员与体育委员,其中甲、乙二人不能担任文娱委员,则不同的选法共有___![]() __种。(用数字作答)
__种。(用数字作答)
11.(重庆理科第15题)某校要求每位学生从7门课程中选修4门,其中甲乙两门课程不能都选,则不同的选课方案有_____![]() ______种。(以数字作答)
______种。(以数字作答)
12.(重庆文科第15题)要排出某班一天中语文、数学、政治、英语、体育、艺术6门课各一节的课程表,要求数学课排在前3节,英语课不排在第6节,则不同的排法种数为 288 。(以数字作答)
13.(陕西理科第16题)安排3名支教老师去6所学校任教,每校至多2人,则不同的分配方案共有 ![]() 种.(用数字作答)
种.(用数字作答)
14.(浙江文科第16题)某书店有11种杂志,2元1本的8种,1元1本的3种.小张用10元钱买杂志(每种至多买一本,10元钱刚好用完),则不同买法的种数是______![]() ____(用数字作答).
____(用数字作答).
15.(江苏第12题)某校开设9门课程供学生选修,其中![]() 三门由于上课时间相同,至多选一门,学校规定每位同学选修4门,共有 75 种不同选修方案。(用数值作答)
三门由于上课时间相同,至多选一门,学校规定每位同学选修4门,共有 75 种不同选修方案。(用数值作答)
16.(辽宁理科第16题)将数字1,2,3,4,5,6拼成一列,记第![]() 个数为
个数为![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,则不同的排列方法有
,则不同的排列方法有 ![]() 种(用数字作答).
种(用数字作答).
17.(宁夏理科第16题)某校安排5个班到4个工厂进行社会实践,每个班去一个工厂,每个工厂至少安排一个班,不同的安排方法共有 ![]() 种.(用数字作答)
种.(用数字作答)
18.已知A={a,b,c},B={-5,0,5},![]() 是A到B的映射,则满足
是A到B的映射,则满足![]() 的映
的映
射共有 7 个。
19、在区间![]() 中随机的取出两个数,则两数之和小于
中随机的取出两个数,则两数之和小于![]() 的概率是 0.68
的概率是 0.68
20.5个大小都不同的实数,按如图形式排列,设第一行中的最大数为a,第二行中的最
 大数为b,则满足a<b的所有排列的个数为(B)
大数为b,则满足a<b的所有排列的个数为(B)
A.144 B.72
C.36 D.24
21.4名男生与5名女生站成一排,要求4名男生的顺序一定,5名女生的顺序也一定,不同的站法总数为(A)
A.126 B.186 C.3024 D.15120
22.用4种不同的颜色对圆上依次排列的![]() ,
,![]() ,
,![]() ,
,![]() 四点染色,每个点染一种颜色,且相邻两点染不同的颜色,则染色方案的总数为(C)
四点染色,每个点染一种颜色,且相邻两点染不同的颜色,则染色方案的总数为(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 23、如图,点P1,P2,P3,…,P10分别是四面体顶点或棱的中点.从点P2,P3,…,P10中选出3个不同点,使它们与顶点P1在同一个平面上,共有 33
种不同选法.
23、如图,点P1,P2,P3,…,P10分别是四面体顶点或棱的中点.从点P2,P3,…,P10中选出3个不同点,使它们与顶点P1在同一个平面上,共有 33
种不同选法.
24.有A、B、C、D、E、F6个集装箱,准备用甲、乙、丙三辆卡车运送,每台卡车一次运两个。若卡车甲不能运A箱,卡车乙不能运B箱,此外无其它任何限制;要把这6个集装箱分配给这3台卡车运送,则不同的分配方案的种数为 (D)
(A) 168 (B) 84 (C) 56 (D) 42
25、两个实数集![]() ,若从A到B的映射
,若从A到B的映射![]() 使得B中每个元素都有原象,且
使得B中每个元素都有原象,且![]() ,则这样的映射共有( B)个
,则这样的映射共有( B)个
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
(二). 二项式定理的通项公式与赋值法的理解及应用;
1.(全国Ⅰ卷理科第10题)![]() 的展开式中,常数项为15,则n= ( D )
的展开式中,常数项为15,则n= ( D )
A.3 B.4 C.5 D.6
2.(重庆理科第4题)若![]() 展开式的二项式系数之和为64,则展开式的常数项为( B )
展开式的二项式系数之和为64,则展开式的常数项为( B )
A10 B.20 C.30 D.120
3.(重庆文科第4题)![]() 展开式中
展开式中![]() 的系数为( B )
的系数为( B )
(A)15 (B)60 (C)120 (D)240
4.(湖北理科第1题)如果![]() 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数![]() 的最小值为( B )
的最小值为( B )
A.3 B.5 C.6 D.10
5.(浙江文科第6题)![]() 展开式中的常数项是( C )
展开式中的常数项是( C )
(A) -36 (B)36 (C) -84 (D) 84
6.(江西理科第4题)已知![]() 展开式中,各项系数的和与其各项二项式系数的和之比为
展开式中,各项系数的和与其各项二项式系数的和之比为![]() ,则
,则![]() 等于( C )
等于( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(江西文科第5题)设![]() ,
,
则![]() 的值为( A )
的值为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(全国Ⅱ卷理科第13题)![]() 的展开式中常数项为
的展开式中常数项为
![]() .(用数字作答)
.(用数字作答)
9.(天津理科第11题)若![]() 的二项展开式中
的二项展开式中![]() 的系数为
的系数为![]() ,则
,则![]()
![]() (用数字作答).
(用数字作答).
10.(安徽文科第12题)已知![]() ,
,
则(![]() 的值等于
的值等于
![]() .
.
11.(辽宁文科第14题)![]() 展开式中含
展开式中含![]() 的整数次幂的项的系数之和为
的整数次幂的项的系数之和为 ![]() (用数字作答).
(用数字作答).
12.若![]() 的展开式中只有第6项的系数最大,则该展开式中的常数项为(C
)
的展开式中只有第6项的系数最大,则该展开式中的常数项为(C
)
A.462 B.252 C.210 D.10
13.已知![]() -5
-5
 14.设
14.设![]()
(其中![]() 为正奇数)则
为正奇数)则![]() -1
;
-1
;
15.设an(n=2,3,4…)是(3+![]() )n的展开式中x的一次项的系数,则
)n的展开式中x的一次项的系数,则![]() (
(![]() +
+![]() +
+
…+![]() )的值是______18______.
)的值是______18______.
(三). .等可能性事件,互斥事件(对立事件),独立事件(独立重复试验)的意义及其概率的求法;
1.从5张100元,3张200元,2张300元的奥运预赛门票中任取3张,则所取3张中至少有2张价格相同的概率为(A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.已知一组抛物线![]() ,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是(B)
,其中a为2,4,6,8中任取的一个数,b为1,3,5,7中任取的一个数,从这些抛物线中任意抽取两条,它们在与直线x=1交点处的切线相互平行的概率是(B)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即以先赢2局者为胜.根据经验,每局比赛中甲获胜的概率为0.6,则本次比赛甲获胜的概率是(D)
(A1 0.216 (B)0.36 (C)0.432 (D)0.648
4.在五个数字![]() 中,若随机取出三个数字,则剩下两个数字都是奇数的概率是
中,若随机取出三个数字,则剩下两个数字都是奇数的概率是
(结果用数值表示).0.3
5.位于坐标原点的一个质点![]() 按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是
按下列规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是![]() ,质点
,质点![]() 移动五次后位`于点
移动五次后位`于点![]() 的概率是(
B )
的概率是(
B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.设集合![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() ,确定平面上的一个点
,确定平面上的一个点![]() ,记“点
,记“点![]() 落在直线
落在直线![]() 上”为事件
上”为事件![]() ,若事件
,若事件![]() 的概率最大,则
的概率最大,则![]() 的所有可能值为( D )
的所有可能值为( D )
A.3 B.4 C.2和5 D.3和4
7.一个总体含有100个个体,以简单随机抽样方式从该总体中抽取一个容量为5的样本,则指定的某个个体被抽到的概率为 .![]()
8.一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球,若从中任取两个球,则取到的都是红球,且至少有1个球的号码是偶数的概率是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.将一骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一袋中装有大小相同,编号分别为![]() 的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为( D )
的八个球,从中有放回地每次取一个球,共取2次,则取得两个球的编号和不小于15的概率为( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.连掷两次骰子得到的点数分别为![]() 和
和![]() ,记向量
,记向量![]() 与向量
与向量![]() 的夹角为
的夹角为![]() ,则
,则![]() 的概率是(
C )
的概率是(
C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.某篮运动员在三分线投球的命中率是![]() ,他投球10次,恰好投进3个球的概率 .(用数值作答)
,他投球10次,恰好投进3个球的概率 .(用数值作答)![]()
13.将5本不同的书全发给4名同学,每名同学至少有一本书的概率是( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
14.甲、乙两个袋中均有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球、2个白球, 乙袋装有1个红球、5个白球.现分别从甲、乙两袋中各随机取出一个球,则取出的两球都是红球的概率为
.(答案用分数表示) ![]()
15.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是(A)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.(二月模拟)甲、乙两人玩数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙想的数字记为
,再由乙猜甲刚才想的数字,把乙想的数字记为![]() ,且
,且![]() ,
,![]() ∈
∈![]() ,若
,若![]() ,则称“甲乙心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为__4/9______.
,则称“甲乙心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为__4/9______.
14.用黑白两种颜色的正方形地砖依照下图的规律
拼成若干图形,现将一粒豆子随机撒在第100个图
中,则豆子落在白色地砖上的概率是 _ . 503/603 。
|
第1个 第2个 第3个
15.在长为10 cm的线段AB上任取一点P,并以线段AP为边作正方形,这个正方形的面积介于25cm2与49 cm2之间的概率为 ______![]() ____________________.
____________________.
16.在平面直角坐标系中,横坐标与纵坐标都在集合A={0,1,2,3,4,5}内任取一个值,则此点正好在直线y=x+1上的概率为 ![]() .
.
 17.如右图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长。在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为
17.如右图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长。在这个图形上随机撒一粒黄豆,它落在扇形外正方形内的概率为
![]() 。(用分数表示)
。(用分数表示)
18. 将甲、乙两颗骰子先后各抛掷一次,a,b分别表示抛掷甲、乙两颗骰子所掷出的点数,若M(a,b)落在不等式x2+y2≤m(m为常数)所表示的区域内,设为事件C,要使事件C的概率P(C)=1,则m的最小值为(72)
19. 在所有的两位数中,任取一个数,则这个数能被2或3整除的概率为 ![]() .
.
20. 甲. 乙两人约定在6时到7时之间在某处会面,并约定先到者
等候另一人15分钟,过时即可离去,则两人会面的概率是
![]() .
.
21、袋中装有编号从1、2、3、4的四个球,四个人从中各取一个球,则甲不取1号球,乙不取2号球,丙不取3号球,丁不取4号球的概率(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
22.9支足球队参加足球预选赛,把9支队伍任意等分成3组,试求两支“冤家队”恰好相逢在同一组的概率 .
23. 一台机床有![]() 的时间加工零件A,
其余时间加工零件B, 加工A时,停机的概率是
的时间加工零件A,
其余时间加工零件B, 加工A时,停机的概率是![]() ,
,
加工B时,停机的概率是![]() , 则这台机床停机的概率为( A
)
, 则这台机床停机的概率为( A
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
24.若m.n均为非负整数,在做m+n的加法时各位均不进位(例如,134+3802=3936),则称(m,n)为“简单的”有序对,而m+n称为有序数对(m,n)的值,那么值为1942的“简单的”有序对的个数是 ( D )
A、20 B、16 C、150 D、300
25.已知A箱内有1个红球和5个白球,B箱内有3个白球,现随意从A箱中取出3个球放入B箱,充分搅匀后再从中随意取出3个球放人4箱,共有___400______种不同的取法,又红球由A箱移人到B箱,再返回到A箱的概率等于__0.25_________.
26、甲、乙两人约定在6时到7时之间在某处会面,并约定先到者应等候另一个人一刻钟,过时即刻离去,两人会面的概率为( D )
A、![]() ; B、
; B、![]() ; C、
; C、![]() ;
D、
;
D、![]()
27、已知A箱内有红球1个和白球(n+1)个,B箱内有白球(n-1)个(n∈N,且n≥2),现随意从A箱中取出3个球放入B箱,将B箱中的球充分搅匀后,再从中随意取出3个球放入A箱,则红球由A箱移到B箱,再返回到A箱的概率等于(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 28.正方体ABCD−A1B1C1D1的各个顶点与各棱的中点共20个
28.正方体ABCD−A1B1C1D1的各个顶点与各棱的中点共20个
点中,任取两点连成直线,在这些直线中任取一条,它与对角线
BD1垂直的概率为 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
29、口袋中放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列![]() ,
, ,如果
,如果![]() 为数列
为数列![]() 的前
的前![]() 项和,那么
项和,那么![]() 的概率为( B )
的概率为( B )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
(四). (理科)离散型随机变量的分布列、数学期望与方差的求法和实际意义;
1.两封信随机投入![]() 三个空邮箱,则
三个空邮箱,则![]() 邮箱的信件数
邮箱的信件数![]() 的数学期望
的数学期望![]() .
.![]()
2.随机变量![]() 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
|
|
其中![]() 成等差数列,若
成等差数列,若![]() ,则
,则![]() 的值是
.
的值是
.![]()
(五). 频率分布表及频率分布条形图、直方图的理解和应用;
1.为了了解某学校学生的身体发育情况,抽查了该校100名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如右图所示.根据此图,估计该校2000名高中男生中体重大于70.5公斤的人数为( B )
A.300 B.360 C.420 D.450


2.根据某水文观测点的历史统计数据,得到某条河流水位的频率分布直方图(如图2).从图中可以看出,该水文观测点平均至少一百年才遇到一次的洪水的最低水位是( C )
A.48米 B.49米 C.50米 D.51米


3.从某自动包装机包装的食盐中,随机抽取![]() 袋,测得各袋的质量分别为(单位:
袋,测得各袋的质量分别为(单位:![]() ):
):
| 492 | 496 | 494 | 495 | 498 | 497 | 501 | 502 | 504 | 496 |
| 497 | 503 | 506 | 508 | 507 | 492 | 496 | 500 | 501 | 499 |
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在497.5g~501.5g之间的概率约为_____.0.25
4.某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;![]() 第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为
第六组,成绩大于等于18秒且小于等于19秒.右图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为![]() ,成绩大于等于15秒且小于17秒的学生人数为
,成绩大于等于15秒且小于17秒的学生人数为![]() ,则从频率分布直方图中可分析出
,则从频率分布直方图中可分析出![]() 和
和![]() 分别为( A )
分别为( A )
A.0.9,35 B.0.9,45
C.0.1,35 D.0.1,45

5.从一堆苹果中任取了20只,并得到它们的质量(单位:克)数据分布表如下:
| 分组 |
|
|
|
|
|
|
| 频数 | 1 | 2 | 3 | 10 | 1 |
则这堆苹果中,质量不小于120克的苹果数约占苹果总数的 %.70
6.(二月模拟)高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
|
| ① | ② |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 | 0.300 |
|
| 0.275 | |
|
| 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(1) 根据上面图表,①②③④处的数值
分别为 ;
(2) 在所给的坐标系中画出[85,155]的频率分布直方图;
(3) 根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.


.解(1) ①1, ②0.025,
③0.1, ④1
(2)直方图如右
(3)利用组中值得
平均数为=90![]() 0.025+100
0.025+100![]() 0.05+110
0.05+110![]() 0.2+120
0.2+120![]() 0.3+130
0.3+130![]() 0.275+140
0.275+140![]() 0.05=122.5 ;
0.05=122.5 ;
7、一个容量为20的样本,已知某组的频率为0.25,则该组频数为( C )
A.80 B.15 C.5 D.2
8. 一组样本数据,容量为150,按从小到大的组序分成5个组,其频数如下表:
| 组号 | 1 | 2 | 3 | 4 | 5 |
| 频数 | 28 | 32 | 28 | 32 | x |
那么,第5组的频率为 0.2
9.某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图). 则这10000人中数学成绩在[140,150]段的约是 800 人. 
10、在抽查产品的尺寸过程中,将其尺寸分成若干组,![]() 是其中的一组,抽查出的个体在该组上的频率为m,该组在频率分布直方图的高为h,则a-b等于。©
是其中的一组,抽查出的个体在该组上的频率为m,该组在频率分布直方图的高为h,则a-b等于。©
A.hm B.![]() C.
C.![]() D.h+m
D.h+m
(六). 简单随机抽样、系统抽样、分层抽样的操作方法以及它们的区别与联系
1.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是(C)
(A)4 (B)5 (C)6 (D)7
2.某校有学生2000人,其中高三学生500人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高三学生的人数为___________.50
3.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是 6 .
4. 从2008名学生中选取100名组成合唱团,若采用下面的方法选取:先用简单随机抽样从2008人中剔除8人,剩下的2000人再按系统抽样的方法进行,则每人被剔除的概率为 ![]() .
.
5. 某校有教师200人,男学生1200人,女学生1000人,现用分层抽样的方法从所有师生中抽取一个容量为n的样本,已知从女学生中抽取的人数为80人,则n的值为![]()
(七). (理科)正态分布与正态曲线的概念与性质的理解并掌握简单应用;
1.以![]() 表示标准正态总体在区间(
表示标准正态总体在区间(![]() )内取值的概率,若随机变量
)内取值的概率,若随机变量![]() 服从正态分布
服从正态分布![]() ,则概率
,则概率![]() 等于(B)
等于(B)
(A)![]() -
-![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
2.设随机变量![]() 服从标准正态分布
服从标准正态分布![]() ,已知
,已知![]() ,则
,则![]() =(
C )
=(
C )
A.0.025 B.0.050 C.0.950 D.0.975
3.在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() .若
.若![]() 在
在![]() 内取值的概率为0.4,则
内取值的概率为0.4,则![]() 在
在![]() 内取值的概率为
.0.8
内取值的概率为
.0.8
4.已知随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() ,则
,则![]() ( A )
( A )
A.![]() B.
B.![]() C.
C.![]() D,
D,![]()
5.随机变量ξ的概率分布规律为P(ξ=n)=(n=1,2,3,4),其中a是常数,则P(<ξ<![]() 的值为( A )
的值为( A )
(A) (B) (C) (D)
5.设随机变量ξ服从正态分布N(0,1),记φ(x)=p(ξ<x),给出下列结论:
①φ(0)=0.5;②φ(x)=1-φ(-x);③p (|ξ|<2)=2φ(2)-1。则正确结论的序号是____①②③_________
6.(理科)某校![]() 名同龄学生的体重
名同龄学生的体重![]() 服从正态分布
服从正态分布![]() ,
,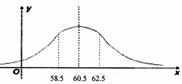 且
且
正态分布的密度曲线如图所示,若![]() ~
~![]()
![]() 体重属于正 常情况, 则这
体重属于正 常情况, 则这![]() 名学生中体重属于正常情况的人数约是(其中
名学生中体重属于正常情况的人数约是(其中 ![]() )(A)
)(A)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设随机变量![]() 服从正态分布N(0,1),设
服从正态分布N(0,1),设![]() ,则下列结论不正确的是(D)
,则下列结论不正确的是(D)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(八). (理科)了解线性回归的概念及性质;
1.(二月模拟)某小卖部为了了解热茶销售量y(杯)与气温x(![]() )之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
| 气温( | 18 | 13 | 10 | -1 |
| 杯数 | 24 | 34 | 38 | 64 |
由表中数据算得线性回归方程![]() 中的
中的![]() ,预测当气温为
,预测当气温为![]() 时,热茶销售量为
时,热茶销售量为
__70__杯.(回归系数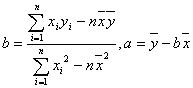 )
)
2、已知x、y之间的一组数据如下:
| x | 0 | 1 | 2 | 3 |
| y | 8 | 2 | 6 | 4 |
则线性回归方程![]() 所表示的直线必经过点 ( (1.5,5) ) .
所表示的直线必经过点 ( (1.5,5) ) .
3.已知x、y的取值如下表所示:
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
从散点图分析,y与x线性相关,且![]() ,则
,则![]() 2.6
.
2.6
.
解答题部分:(理科题):
| 分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 合计 |
|
1.(本小题满分12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如右表:
(I)在答题卡上完成频率分布表,并在给定的坐标系中画出频率分布直方图;
(II)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此,估计纤度的期望.
)作为代表.据此,估计纤度的期望.
2.(本小题满分12分)
袋中装有大小相同的3个红球和2个白球,从袋中随机取球,设取到一个红球得2分,
取到一个白球得1分.现从袋中每次取出一个球,记住得分后放回再次取出一个球·
(Ⅰ)求连续取3次球,恰得3分的概率;
(Ⅱ)求连续取2次球的得分ξ的分布列及期望.
3.(二月模拟)盒子中装着有标数字1,2,3,4,5的上卡片各2张,从盒子中任取3张卡片,按3张卡片上最大数字的8倍计分,每张卡片被取出的可能性都相等,用![]() 表示取出的3张卡片上的最大数字,求:
表示取出的3张卡片上的最大数字,求:
(1)取出的3张卡片上的数字互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分不小于20分的概率.
4.(本小题满分12分)
某电视台“挑战主持人”节目的挑战者闯关时,需要回答两个问题,其中第一个问题回答正确得10分,回答不正确得0分;第二个问题,回答正确得20分,回答不正确得一10分.如果一位挑战者回答第一题正确的概率是0.8,回答第二题正确的概率为0.6,且各题回答正确与否相互之间没有影响.
(1)求这位挑战者总得分![]() 不为负分(即
不为负分(即![]() )的概率;
)的概率;
(2)求这位挑战者回答这两个问题的总得分的概率分布和数学期望.
5. (本小题满分13分)
在医学生物学试验中,经常以果蝇作为试验对象,一个关有6只果蝇的笼子里,不慎混入了两只苍蝇(此时笼内共有8只蝇子:6只果蝇和2只苍蝇),只好把笼子打开一个小孔,让蝇子一只一只地往外飞,直到两只苍蝇都飞出,再关闭小孔.以ξ表示笼内还剩下的果蝇的只数.
(Ⅰ)写出ξ的分布列(不要求写出计算过程);
(Ⅱ)求数学期望Eξ;
(Ⅲ)求概率P(ξ≥Eξ).
.
6.(本小题共13分)
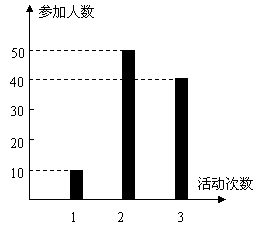 某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
某中学号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(I)求合唱团学生参加活动的人均次数;
(II)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.
(III)从合唱团中任选两名学生,用![]() 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
.
7.(本小题满分12分)
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生
(吨)与相应的生
产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
|
| | | | |
| | | | | |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性
回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:![]() )
)
8.(本小题满分12分)
某陶瓷厂准备烧制甲、乙、丙三件不同的工艺品,制作过程必须先后经过两次烧制,当第一次烧制合格后方可进入第二次烧制,两次烧制过程相互独立.根据该厂现有的技术水平,经过第一次烧制后,甲、乙、丙三件产品合格的概率依次为![]() ,
,![]() ,
,![]() ,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为
,经过第二次烧制后,甲、乙、丙三件产品合格的概率依次为![]() ,
,![]() ,
,![]() .
.
(1)求第一次烧制后恰有一件产品合格的概率;
(2)经过前后两次烧制后,合格工艺品的个数为![]() ,求随机变量
,求随机变量![]() 的期望.
的期望.
9.(本小题满分12分)
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(I)任选1名下岗人员,求该人参加过培训的概率;
(II)任选3名下岗人员,记![]() 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求![]() 的分布列和期望.
的分布列和期望.
10.(本小题满分12分)
某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为
的分布列为
|
| 1 | 2 | 3 | 4 | 5 |
|
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.![]() 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件![]() :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率![]() ;
;
(Ⅱ)求![]() 的分布列及期望
的分布列及期望![]() .
.
11..(本小题满分12分)
如图,面积为![]() 的正方形
的正方形![]() 中有一个不规则的图形
中有一个不规则的图形![]() ,可按下面方法估计
,可按下面方法估计![]() 的面积:在正方形
的面积:在正方形![]() 中随机投掷
中随机投掷![]() 个点,若
个点,若![]() 个点中有
个点中有![]() 个点落入
个点落入![]() 中,则
中,则![]() 的面积的估计值为
的面积的估计值为![]() ,假设正方形
,假设正方形![]() 的边长为2,
的边长为2,![]() 的面积为1,并向正方形
的面积为1,并向正方形![]() 中随机投掷
中随机投掷![]() 个点,以
个点,以![]() 表示落入
表示落入![]() 中的点的数目.
中的点的数目.
(I)求![]() 的均值
的均值![]() ;
;
(II)求用以上方法估计![]() 的面积时,
的面积时,![]() 的面积的估计值与实际值之差在区间
的面积的估计值与实际值之差在区间![]() 内的概率.
内的概率.
附表:![]()
|
|
|
|
|
|
|
|
|
|
|
|
12、袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() .现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止.每个球在第一次被取出的机会是等可能的,用
.现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,…,取后不放回,直到两人中有一人取到白球时即终止.每个球在第一次被取出的机会是等可能的,用![]() 表示取球终止时所需要的取球次数.求:
表示取球终止时所需要的取球次数.求:
(1)袋中原有白球的个数;(2)随机变量![]() 的数学期望;(3)甲取到白球的概率.
的数学期望;(3)甲取到白球的概率.
13.(本小题满分13分,其中(Ⅰ)小问4分,(Ⅱ)小问9分)
某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆![]() 元的保险金,对在一年内发生此种事故的每辆汽车,单位可获
元的保险金,对在一年内发生此种事故的每辆汽车,单位可获![]() 元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为
元的赔偿(假设每辆车最多只赔偿一次),设这三辆车在一年内发生此种事故的概率分别为![]() ,
,![]() ,
,![]() ,且各车是否发生事故相互独立,求一年内该单位在此保险中:
,且各车是否发生事故相互独立,求一年内该单位在此保险中:
(Ⅰ)获赔的概率;
(Ⅱ)获赔金额![]() 的分布列与期望.
的分布列与期望.
14.(本小题满分12分)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数![]() 的分布列及期望
的分布列及期望![]() ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
15.(本小题满分12分)
有一种舞台灯,外形是正六棱柱,在其每一个侧面上安装5只颜色各异的彩灯,假若每只灯正常发光的概率为![]() . 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需要100元,用ξ表示维修一次的费用.
. 若一个面上至少有3只灯发光,则不需要维修,否则需要更换这个面.假定更换一个面需要100元,用ξ表示维修一次的费用.
(Ⅰ)求恰好有2个面需要维修的概率;
(Ⅱ)写出ξ的分布列,并求ξ的数学期望.
16..(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
17.(本题满分12分)
有三个盒子,第一个盒里装有4个红球和1个黑球,第二个盒里装有3个红球2个黑球,第三个盒里装有2个红球3个黑球.如果先从这三个盒子中任取一个,再从中取出的盒子中任取3个球,以![]() 表示所取到的红球个数,求
表示所取到的红球个数,求
(文科)![]() 的概率及
的概率及![]() 的概率.
的概率.
(理科)![]() 的概率分布列及其数学期望.
的概率分布列及其数学期望.
18.(本小题满分12分)
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为![]() 、
、![]() 、
、![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
19.(本小题满分12分)
设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程![]() 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
20.(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件![]() :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率![]() .
.
(1)求从该批产品中任取1件是二等品的概率![]() ;
;
(2)若该批产品共100件,从中任意抽取2件,![]() 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求![]() 的分布列.
的分布列.
21. (12分) 一项"过关游戏"规则规定: 在第n 关要抛掷骰子n次, 若这n次抛掷所出现的点数之和大于2n-1+1 (n∈N*), 则算过关.
(1)求在这项游戏中第三关过关的概率是多少?
(2) (理) 若规定n≤3, 求某人的过关数ξ的期望.
概率理科答案:
1.本小题主要考查频率分布直方图、概率、期望等概念和用样本频率估计总体分布的统计方法,考查运用概率统计知识解决实际问题的能力.
解:(Ⅰ)
| 分组 | 频数 | 频率 |
|
| 4 | 0.04 |
|
| 25 | 0.25 |
|
| 30 | 0.30 |
|
| 29 | 0.29 |
|
| 10 | 0.10 |
|
| 2 | 0.02 |
| 合计 | 100 | 1.00 |
 |
(Ⅱ)纤度落在![]() 中的概率约为
中的概率约为![]() ,纤度小于1.40的概率约为
,纤度小于1.40的概率约为![]() .
.
(Ⅲ)总体数据的期望约为
![]()
2.

3.解:(1)记"一次取出的3张卡片上的数字互不相同的事件"为A,
则![]()
(2)由题意![]() 有可能的取值为:2,3,4,5
有可能的取值为:2,3,4,5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以随机变量![]() 的概率分布为:
的概率分布为:
| | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
所以![]() 的数学期望为E
的数学期望为E![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]()
(3)"一次取出的3张卡片所得分不低于20分"为事件C
![]()
答:
4.解:(1)如果两个题目均答错,得0+(一10)=一10分。
![]()
这位挑战者总得分不为负分的概率为
![]() ……………4分
……………4分
(2)如果两个题目均答错,得0+(一10)=一10分.
如果两个题目一对一错,包括两种情况:
①第一个对,第二个错,得10+(一10)=0分;
②第一个错,第二个对,得0+20=20分;
如果两个题目均答对,得10+20=30分.
故![]() 的可能取值为:一10,0,20,30。
的可能取值为:一10,0,20,30。
![]() ;
;![]()
![]() ;
;![]() ……………8分
……………8分
所以![]() 的概率分布为
的概率分布为
|
| 一10 | 0 | 20 | 30 |
|
| 0.08 | 0.32 | 0.12 | 0.48 |
根据![]() 的概率分布,可得
的概率分布,可得![]() 的期望
的期望
![]() ……………12分
……………12分
5.本小题主要考查等可能场合下的事件概率的计算、离散型随机变量的分布列、数学期望的概念及其计算,考查分析问题及解决实际问题的能力.本小题满分13分.
解:(Ⅰ)![]() 的分布列为:
的分布列为:
|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
|
|
(Ⅱ)数学期望为![]() .
.
(Ⅲ)所求的概率为![]()
6.(共13分)
解:由图可知,参加活动1次、2次和3次的学生人数分别为10、50和40.
(I)该合唱团学生参加活动的人均次数为![]() .
.
(II)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为![]() .
.
(III)从合唱团中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件![]() ,“这两人中一人参加2次活动,另一人参加3次活动”为事件
,“这两人中一人参加2次活动,另一人参加3次活动”为事件![]() ,“这两人中一人参加1次活动,另一人参加3次活动”为事件
,“这两人中一人参加1次活动,另一人参加3次活动”为事件![]() .易知
.易知
![]()
![]() ;
;
![]()
![]() ;
;
![]() 的分布列:
的分布列:
|
| 0 | 1 | 2 |
|
|
|
|
|
![]() 的数学期望:
的数学期望:![]()
7. 解: (1)如下图

(2) =3
=3![]() 2.5+4
2.5+4![]() 3+5
3+5![]() 4+6
4+6![]() 4.5=66.5
4.5=66.5
![]() =
=![]() =4.5
=4.5
![]() =
=![]() =3.5
=3.5
![]() =
=![]() +
+![]() +
+![]() +
+![]() =86
=86
![]()
![]()
故线性回归方程为y=0.7x+0.35
(3)根据回归方程的预测,现在生产100吨产品消耗的标准煤的数量为0.7![]() 100+0.35=70.35
100+0.35=70.35
故耗能减少了90-70.35=19.65(吨)
8.解:分别记甲、乙、丙经第一次烧制后合格为事件![]() ,
,![]() ,
,![]() ,
,
(1)设![]() 表示第一次烧制后恰好有一件合格,则
表示第一次烧制后恰好有一件合格,则
![]()
![]() .
.
(2)解法一:因为每件工艺品经过两次烧制后合格的概率均为![]() ,
,
所以![]() ,
,
故![]() .
.
解法二:分别记甲、乙、丙经过两次烧制后合格为事件![]() ,则
,则
![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
于是,![]() .
.
9.解:任选1名下岗人员,记“该人参加过财会培训”为事件![]() ,“该人参加过计算机培训”为事件
,“该人参加过计算机培训”为事件![]() ,由题设知,事件
,由题设知,事件![]() 与
与![]() 相互独立,且
相互独立,且![]() ,
,![]() .
.
(I)解法一:任选1名下岗人员,该人没有参加过培训的概率是
![]()
所以该人参加过培训的概率是![]() .
.
解法二:任选1名下岗人员,该人只参加过一项培训的概率是
![]()
该人参加过两项培训的概率是![]() .
.
所以该人参加过培训的概率是![]() .
.
(II)因为每个人的选择是相互独立的,所以3人中参加过培训的人数![]() 服从二项分布
服从二项分布![]() ,
,![]() ,
,![]() ,即
,即![]() 的分布列是
的分布列是
|
| 0 | 1 | 2 | 3 |
|
| 0.001 | 0.027 | 0. 243 | 0.729 |
![]() 的期望是
的期望是![]() .
.
(或![]() 的期望是
的期望是![]() )
)
10.解:
(Ⅰ)由![]() 表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
表示事件“购买该商品的3位顾客中至少有1位采用1期付款”.
知![]() 表示事件“购买该商品的3位顾客中无人采用1期付款”
表示事件“购买该商品的3位顾客中无人采用1期付款”
![]() ,
,
![]() .
.
(Ⅱ)![]() 的可能取值为
的可能取值为![]() 元,
元,![]() 元,
元,![]() 元.
元.
![]() ,
,
![]() ,
,
![]() .
.
![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
![]()
![]() (元).
(元).
11.解:
每个点落入![]() 中的概率均为
中的概率均为![]() .
.
依题意知![]() .
.
(Ⅰ)![]() .
.
(Ⅱ)依题意所求概率为![]() ,
,
![]()
![]()
![]()
![]() .
.
12、【解】(1)设袋中原有n个白球,由题意知:
 .
.
∴![]() ,解得
,解得![]() 或
或![]() (舍去),即袋中原有3个白球.……4分
(舍去),即袋中原有3个白球.……4分
(2)由题意,![]() 的可能取值为1,2,3,4,5,
的可能取值为1,2,3,4,5,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
所以,取球次数![]() 的分布列为:
的分布列为:
|
| 1 | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
|
![]() ……8分
……8分
(3)因为甲先取,所以甲只有可能在第1次,第3次和第5次取球,记“甲取到
白球”的事件为A,则![]() ,
,
因为事件![]() 两两互斥,所以
两两互斥,所以
![]() .……12分
.……12分
13.(本小题13分)
解:设![]() 表示第
表示第![]() 辆车在一年内发生此种事故,
辆车在一年内发生此种事故,![]() .由题意知
.由题意知![]() ,
,![]() ,
,![]() 独立,
独立,
且![]() ,
,![]() ,
,![]() .
.
(Ⅰ)该单位一年内获赔的概率为
![]() .
.
(Ⅱ)![]() 的所有可能值为
的所有可能值为![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]() ,
,
![]()
![]() .
.
综上知,![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
|
|
|
求![]() 的期望有两种解法:
的期望有两种解法:
解法一:由![]() 的分布列得
的分布列得
![]()
![]() (元).
(元).
解法二:设![]() 表示第
表示第![]() 辆车一年内的获赔金额,
辆车一年内的获赔金额,![]() ,
,
则![]() 有分布列
有分布列
|
|
|
|
|
|
|
|
故![]() .
.
同理得![]() ,
,![]() .
.
综上有![]() (元).
(元).
14.本题考察相互独立事件、互斥事件等的概率计算,考察随机事件的分布列,数学期望等,考察运用所学知识与方法解决实际问题的能力。
解:(Ⅰ)记“厂家任取4件产品检验,其中至少有1件是合格品”为事件A
用对立事件A来算,有![]()
(Ⅱ)![]() 可能的取值为
可能的取值为![]()
![]() ,
,![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
![]()
记“商家任取2件产品检验,都合格”为事件B,则商家拒收这批产品的概率
![]()
所以商家拒收这批产品的概率为![]()
15.解:(Ⅰ)因为一个面不需要维修的概率为![]() ,
,
所以一个面需要维修的概率为![]() .
……3分
.
……3分
因此,六个面中恰好有2个面需要维修的概率为![]() . ……6分
. ……6分
(Ⅱ)因为![]() ~
~![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以维修一次的费用![]() 的分布为:
的分布为:
|
| 0 | 100 | 200 | 300 | 400 | 500 | 600 |
| P |
|
|
|
|
|
|
|
……10分
因为![]() ~
~![]() ,所以
,所以![]() 元.
元.
16.本小题主要考查互斥事件、相互独立事件、离散型随机变量的分布列和数学期望等基础知识,考查运用概率知识解决实际问题的能力.满分12分.
(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件![]() ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件![]() .由于事件
.由于事件![]() 相互独立,且
相互独立,且![]() ,
,![]() .
.
故取出的4个球均为黑球的概率为![]() .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件![]() ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件![]() .由于事件
.由于事件![]() 互斥,
互斥,
且![]() ,
,![]() .
.
故取出的4个球中恰有1个红球的概率为![]() .
.
(Ⅲ)解:![]() 可能的取值为
可能的取值为![]() .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得![]() ,
,![]() ,
,
![]() .从而
.从而![]() .
.
![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
17.设![]() 表示从三个盒子中取出第
表示从三个盒子中取出第![]() 个盒子时,
个盒子时,![]() 的概率,
的概率,![]() ;
;![]()
∵从三个盒子中任取一个盒子的概率为![]()
∴![]() =
=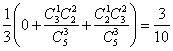
![]() =
=
![]() =
=
(文科)∴![]() ,
,![]() …12分
…12分
(理科)依题意知![]() ,
,
![]() =
=
|
| 0 |
|
|
|
|
|
|
|
|
|
∴
![]()
18.(本小题满分12分)
解法一:(Ⅰ)记“该选手能正确回答第![]() 轮的问题”的事件为
轮的问题”的事件为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() 该选手被淘汰的概率
该选手被淘汰的概率
![]()
![]() .
.
(Ⅱ)![]() 的可能值为
的可能值为![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() 的分布列为
的分布列为
|
| 1 | 2 | 3 |
|
|
|
|
|
![]() .
.
解法二:(Ⅰ)记“该选手能正确回答第![]() 轮的问题”的事件为
轮的问题”的事件为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
![]() 该选手被淘汰的概率
该选手被淘汰的概率![]()
![]() .
.
(Ⅱ)同解法一.
19.【标准答案】:(I)基本事件总数为![]() ,
,
若使方程有实根,则![]() ,即
,即![]() 。
。
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
目标事件个数为![]()
因此方程![]() 有实根的概率为
有实根的概率为![]()
(II)由题意知,![]() ,则
,则
![]() ,
,![]()
![]() ,
,
故![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
| P |
|
|
|
![]() 的数学期望
的数学期望![]()
(III)记“先后两次出现的点数中有5”为事件M,“方程![]() 有实根” 为事件N,则
有实根” 为事件N,则![]() ,
,![]() ,
,
![]() .
.
20.解:(1)记![]() 表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中无二等品”,
![]() 表示事件“取出的2件产品中恰有1件二等品”.
表示事件“取出的2件产品中恰有1件二等品”.
则![]() 互斥,且
互斥,且![]() ,故
,故
![]()
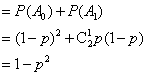
于是![]() .
.
解得![]() (舍去).
(舍去).
(2)![]() 的可能取值为
的可能取值为![]() .
.
若该批产品共100件,由(1)知其二等品有![]() 件,故
件,故
![]() .
.
![]() .
.
![]() .
.
所以![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 |
|
|
|
|
|
21.解(1)设第三关不过关事件为A, 则第三关过关事件为 .由题设可知: 事件A是指第三关出现点数之和没有大于5.因为第三关出现点数之和为3,4, 5的次数分别为1,3,6知:
P(A)= = , ∴P()=1- = .
(2)设第一关不过关的事件为B, 第二关不过关的事件为C.依题意, 得P(B)= = , P()=郝进制作
P( C) = = , P()=1- = . ∵n≤3, ∴ξ的取值分别为0,1,2,3
∴P(ξ=0)=P(B)= , P(ξ=1)=P(·C )= ×=
P(ξ=2)= P(··A) = ×× =
P(ξ=3)= P(··) = ××=
| ξ | 0 | 1 | 2 | 3 |
| P |
故ξ的分布列:
郝 进制作
Eξ=0×+1×+2×+3×=

