高考理科数学模拟试题三（理科）2008-3-6
班级 姓名
一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个是符合题目要求的．
1.如果复数
是纯虚数，那么实数
等于( )
A.-1 B.0 C.0或1 D.0或-1
2．．已知集合
，R是实数集，则（
）∩A=（ ）
A．[0，1] B．
C．
D．以上都不对
3．已知两个不同的平面
、
和两条不重合的直线m、n，有下列四个命题
①若
②若
③
④
其中正确命题的个数是（ ）
A．0个 B．1个 C．2个 D．3个
4. 已知两向量
的夹角为60°，且
在△ABC中，
，
则A的值为 （ ）
A．120° B．30° C．150° D．60°
5．已知等差数列{an}是单调数列，且a1,a3,a4,成等比数列，Sn为数列{an}的前n项和，则
的值为 （ ）
A．3 B．2 C．1 D．不能确定
6．下图是某公交线路收支差额y与乘客量x之间的关系图（收支差额=车票收入+财政补贴-支出费用；假设财政补贴和支出费用与乘客量无关），在这次公交、地铁票价听证会上，有市民代表提出“增加财政补贴，票价实行8折优惠”的建议.则下列四个图像反映了市民代表建议的是 （ ）
|
A． B． C． D．
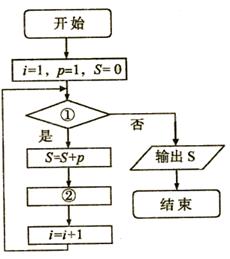
7．给出50个数，1，2，4，7，11，…，其规律是： 第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，以此类推，要计算这50个数的和.现已给出了该 问题算法的程度框图如图，请在图中判断框中的 ①处和执行框中的②处填上合适的语句，使之能完成该题算法功能（ ）
A．i≤50；p=p+I B．i<50；p=p+I C．i≤50；p=p+1 D．i<50；p=p+1
8．函数f ( x ) = Asin (
x +
)( A＞0，>0)的部分图象如图所示，则f ( 1 ) + f ( 2 ) + … + f ( 2
006 )的值等于（ ）
A．0 B．
C．2 + D．2–
9.
与面成30°和45°的角且面ABC与面成60°的二面角，那么
的值为( )
A．1
B．
C．
D．1或
10．若
，则k的取值范围是 （ ）
A．
B．
C．
D．
11．如果椭圆
上存在一点P，使点P到左准线的距离与它到右焦点的距离相等，那么椭圆的离心率的范围是（
）
A 
B 
C 
D 
12．已知函数
若方程
有且只有两个不相等的实数根，则实数a的取值范围为（
）
A．
B．
C．
D．
二、填空题：本大题共4个小题，每小题5分，共计20分。把答案填在题中横线上。
13．已知
是抛物线
的准线与双曲线
的两条渐近线所围成的三角形平面区域内（含边界）的任意一点，则
的最大值为
14．有一地球同步卫星A与地面四个科研机构B、C、D、E，它们两两之间可以相互接发信息，由于功率有限，卫星及每个科研机构都不能同时向两处发送信息（例如A不能同时给B、C发信息，它可先发给B，再发给C），它们彼此之间一次接发信息的所需时间如右图所示．则一个信息由卫星。则一个信息由卫星发出到四个科研机构都接到该信息时所需的最短时间为________．
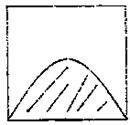
15．如图所示，墙上挂有一块边长为2的正方形木板，上面画有振幅为1的正弦曲线半个周期的图案（阴影部分）．某人向此板投镖，假设每次都能击中木板并且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是_________.
16．(1)已知命题：“若数列
为等差数列，且
，则
”，现已知数列
为等比数列，且
，若类比上述结论，则可得
。
(2)（选做题）．不等式
的解集非空，则
的取值范围为___________．
临沂市兰山高考补习学校2007-2008学年下学期高三
数学模拟试题三（理科）2008-3-6
班级 姓名
三、解答题：本大题共6小题，满分70分。解答应写出文字说明、证明过程或推演步骤。
17．已知
、
是两个不共线的向量且
，
。
（1）求证：
与
垂直；
（2）若
，
，且
，求
。
18．一个口袋里面装有２个白球４个黑球，这些球除颜色差别外没有其它的区别. 现在从袋中随机取出一个来记好颜色，然后放回并搅匀，之后再随机取球记色，再放回搅匀，…. 记数列
，数列
的前n项和记为
①.求事件“
＝２”的概率； ②求取值的分布列和数学期望
.
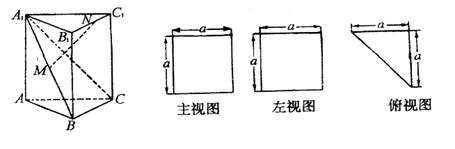
19．一个多面体的直观图（主观图、左视图、俯视图）如图所示，M、N分别为A1B1、B1C1的中点.
（1）求证：MN∥平面ACC1A1；
（2）求证：MN⊥平面A1BC；
（3）求二面角A—A1B—C的大小.
20．已知函数
（m、n∈R，m≠0）的图像在（2，
）处的切线与x轴平行．
（1）求n，m的关系式并求
的单调减区间；
（2）证明：对任意实数
关于x的方程：
恒有实数解．
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数是在闭区间[a,b]上连续不断的函数，且在区间（a,b）内导数都存在，则在（a,b）内至少存在一点x0，使得
如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
当
时，
（可不用证明函数的连续性和可导性）
21．如图：已知椭圆
是长轴的一个端点，弦BC过椭圆的中心O，且
.
（1）求椭圆的方程；
（2）对于椭圆上的两点P、Q，∠PCQ的平分线总是垂直于x轴时，是否存在实数λ，使得
22．
（A）设
（
（1）求
的值；
（2）求证：数列是等比数列;
（3）设数列的前n项和为
的大小.
(B)已知函数
(1)
若函数在其定义域内为单调函数，求实数a的取值范围;
(2)
若函数的图象在x=1处的切线的斜率为0，且
，
①若
;
②若
与
的大小，并说明你的理由
数学模拟试题二（理科）参考答案2008-3-6
一、选择题
DADCB, BABDB, AC
二、填空题
13. 5 14. 6 15. 
16.(1) 
(2) 
三、解答题
17解
18．解：（１）事件
只能是“四次取球中出现三次白球一次黑球”，
每次取得白球的概率为
；取得黑球的概率是
…………..2’
于是
………………………………..2’
（２）可能的取值有
；
；
；
；
，…………………5’
|
|
|
| ０ | ２ | ４ |
|
|
|
|
|
|
|
于是取值的分布列为
………………………………………….2’
…………2’
19．解：由题意可知，这个几何体是直三棱柱，且AC⊥BC，AC=BC=CC1.
（1）连结AC1，AB1.
由直三棱柱的性质得AA1⊥平面A1B1C1，
所以AA1⊥A1B1，则四边形ABB1A1为矩形.
由矩形性质得AB1过A1B的中点M.
在△AB1C1中，由中位线性质得MN//AC1，
又AC1
平面ACC1A1，MN
平面ACC1A1，
所以MN//平面ACC1A1.………………………………4分
（2）因为BC⊥平面ACC1A1，AC平面ACC1A1，
所以BC⊥AC1.
在正方形ACC1A1中，A1C⊥AC1.
又因为BC∩A1C=C，所以AC1⊥平面A1BC.
由MN//AC1，得MN⊥平面A1BC.………………………………8分
（3）由题意CB，CA，CC1两两垂直，故可以C为的点，
CB，CA，CC1所在直线分别为x轴，y轴，z轴建立空间直角坐标系，
又AC = BC = CC1 = a，
则
则AB中点E的坐标为
，
为平面AA1B的法向量.
又AC1⊥平面A1BC，故
为平面A1BC的法向量 …………………………10分
设二面角A—A1B—C的大小为θ，
则
由题意可知，θ为锐角，所以θ= 60°，即二面角A—A1B—C为60°……12分
20．解：（1）因为
1分
由已知
2分
即
当
3分
当
4分
综上所述：当
当
5分
（2）
6分
可化为
令
7分
则
，
，
即
又因为
所以
，即
8分
故
在区间
内必有解，即关于x的方程
恒有实数解 9分
（3）令
10分
则
符合拉格朗日中值定理的条件，即存在
使
11分
因为
即
12分
21．（I）解：
又
∴△AOC是等腰直角三角形
∵A（2，0），∴C（1，1）而点C在椭圆上，
∴
∴所求椭圆方程为
（Ⅱ）对于椭圆上两点P、Q，∵∠PCQ的平分线总是垂直于x轴
∴PC与CQ所在直线关于x=1对称，kpC=k，则kcQ=－k，
设C（1，1），则PC的直线方程y－1=k(x－1)
y=k(x－1)+1 ①
QC的直线方y－1=－k(x－1) y=－k(x－1)+1 ②
将①代入得(1+3k2)x2－6k(k－1)x+3k2－6k－1=0 ③
∵C（1，1）在椭圆上，∴x=1是方程③的一个根，
∴xp·1=
=1同理将②代入x2+3y2=4得
（1+3k2）x2－6k(k+1)x+3k2+6k－1=0 ④
∵C（1，1）在椭圆上，
∴x=1是方程④的一个根，
∴xQ·1= 
∴存在实数λ，使得
.
22．(A)解：（1）
…………1分
…………4分
（2）
…………5分
…………7分
为公比的等比数列. …………8分
（3）由（2）知
………5分
…………11分
…………13分
…………14分
22(B) （１）
．．．．．．．．（２分）
①当
时，则有
恒成立。即
②当
时，由x>0,知
恒成立；
内为单调函数，的取值范围为
..….….5分
（2）
函数的图象在
处的切线为斜率为0，
，
………7分
①
用数学归纳法证明：（Ⅰ）当
时，
，不等式成立；
（Ⅱ）假设当时
时，不等式成立，即
那么，
也就是说，当
时，
，根据（Ⅰ）（Ⅱ）对于所有
有，
………………………….10分
②
由
及①，对
有：
……………12分
而
，于是：当
时
………14分