08届高考理科数学第二次联考试卷
数 学（理科）
本试卷共21小题，满分150分．考试用时120分
一、选择题：本大题共8小题，每小题5分，满分40分，在每小题给出的四个选项中，只有一项是符合要求的．
1、设
，
，则
（ ）
A、
B、
C、
D、
2、如图所示，角
的正切线为有向线段（ ）
A、
B、
C、
D、
3、命题“对任意
”的否定是（ ）
A、不存在
B、存在
C、存在
D、对任意的
4、若数列
满足
（
为正常数，
），则称为“等方比数列”．
甲：数列是等方比数列； 乙：数列是等比数列，则（ ）
A、甲是乙的充分条件但不是必要条件 B、甲是乙的必要条件但不是充分条件
C、甲是乙的充要条件 D、甲既不是乙的充分条件也不是乙的必要条件
5、已知双曲线的离心率为
，焦点是
，
，则双曲线方程为（ ）
A、
B、
C、
D、
6、一个长方体共一个顶点的三个面的面积分别是
、
、
，长方体对角线的长为（ ）
A、2
B、3 C、6
D、
7、直角坐标系
中，
分别是与
轴正方向同向的单位向量．在直角三角形
中，若
，则
的可能值个数是（ ）
A、1 B、2 C、3 D、4
8、已知函数
,若
,且
,则有 ( )
A、
B、 
C、
D、
的大小不确定.
二、填空题：本大题共7小题，每小题5分，满分30分．其中13、14、15题是选做题，考生只能选做二题，三题全答的，只计算前两题得分．
9、已知
则
=______________________.
10、已知平面上三点A、B、C满足
，
，
，
则
的值是____________________.
11、一个正整数数表如下（表中下一行中的数的个数是上一行中数的个数的2倍）：
| 第1行 | 1 |
| 第2行 | 2 3 |
| 第3行 | 4 5 6 7 |
| … | … |
则第9行中的第4个数是__________________.
12、 函数
的图像为
，如下结论中正确的是 _________
（写出所有正确结论的编号）．
①图像关于直线
对称； ②图像关于点
对称；
③函数
在区间
内是增函数；
④由
的图像向右平移
个单位长度可以得到图像．
13、（坐标系与参数方程选做题）椭圆
的离心率是_______．
14、（不等式选讲选做题）设函数
，则
；
若
， 则
的取值范围是
．
15、（几何证明选讲选做题）
如图，⊙O上三点A、B、C，PC切⊙O于点C，
∠ABC=1000，∠BCP=500，则∠AOB=_______.
广州市真光中学、肇庆一中2008届高三第二次联考试卷
数学（理科）答卷
二、填空题：9、________ 10、________ 11、________ 12、________
13、________ 14、_________ ________ 15、________
三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．
16、(本题满分12分)已知平面向量 
， 
（
）. 
（Ⅰ）若
，求的值； （Ⅱ）若
，求
.
17、（本题满分12分）数列
中，
，
（
是常数，
），且
成公比不为
的等比数列．（I）求的值；（II）求数列的通项公式．
18、（本题满分14分）在直角坐标系
中，以
为圆心的圆与直线
相切．
（1）求圆的方程； （2）圆与轴相交于
两点，圆内一动点
使
成等比数列， 求
的取值范围．
19、(本题满分14分)已知函数
的图象关于y轴对称，且满足
. （Ⅰ）求函数
的解析式；
（Ⅱ）
，问是否存在
使F(x)在区间
上
是减函数，且在区间（－3,0）内是增函数？试证明你的结论。
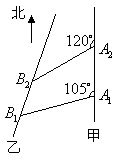
20、（本题满分14分）如图，甲船以每小时
海里的速度向正北方航行，乙船按固定方向匀速直线航行，当甲船位于
处时，乙船位于甲船的北偏西
方向的
处，此时两船相距
海里，当甲船航行分钟到达
处时，乙船航行到甲船的北偏西
方向的
处，此时两船相距
海里，问乙船每小时航行多少海里？
 |
21、（本题满分14分）
已知函数
（
）。
（Ⅰ）若
且
，则称
为
的实不动点，求的实不动点；
（Ⅱ）在数列
中，
，
（
），求数列的通项公式。
数学（理科）参考答案及评分意见
一、选择题： C D C B A D B C
二、填空题： 9、 
；
10、-25
； 11、 259 ； 12、 ①②③ ；
13、
； 14、 6, 
；
15、
三、解答题：
16、解：（Ⅰ）若 ，则
·
.
整理得
，解得：
或
.
……………4分
（Ⅱ）若 ，则有
，即 
.
解得：
或
.
…………………………………8分
当时，
，
；
∴=
=
.
…………10分
当时，
，
；
∴=
=
. ……12分
17、解：（I），
，
，因为
，
，
成等比数列，
所以
， 解得
或
．
………4分
当时，
，不符合题意舍去，故．
………6分
（II）当
时，由于
，
，
，
所以
．
………10分
又，，故
．
当
时，上式也成立，所以
．
………12分
18、解：（1）依题设，圆的半径
等于原点到直线的距离，
即 
． 得圆的方程为
…………5分
（2）不妨设
．由
即得:
． ……6分
设
，由成等比数列，得
，即 
． …………………9分
…………………11分
由于点在圆内，故
由此得
． …………………13分
所以的取值范围为
．
…………………14分
19.解：（Ⅰ）令x－2＝t，则x＝t＋2 ………………1分
由于
，
所以 
∴ 
………………3分
∵ 
的图像关于y轴对称 ∴ 
且 
，即
故 
……………………6分
（Ⅱ）解法一:
……………………7分
设存在，使F(x)满足题目要求，则当－∞＜x1＜x2≤－3时，F(x)是减函数，即
由假设－x1>－x2≥3＞0， ∴ 
∴ 
… … … … … ①
又 
∴ 
∴ 
要使①式恒成立，只须
≥0 即≤
………………10分
又当
时，F(x)是增函数，
即 F(x1)－F(x2)＜0，也就是
… … ②
此时 
， 
要使②式恒成立，只须 
≤0 即 ≥ ……………13分
故存在＝满足题目要求。
……………14分
（Ⅱ）解法二： 依题意F(－3)是F(x)的极小值， ∴ 
……7分
∵ 
，
∴ 
，即
.
……………10分
当＝时，
，
∴当
时，
在
上是减函数；当
时，
是增函数。
故存在满足题目要求。
…………………14分
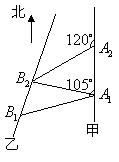20、解法一：如图，连结
，由已知
，
， ………………2分
又
，
是等边三角形，
，………4分
由已知，
，
，
在
中，由余弦定理，
……8分
……………10分
=200 
．
因此，乙船的速度的大小为
（海里/小时）．………………13分
答：乙船每小时航行海里．
………………14分
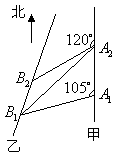
解法二：如图，连结
，由已知
，，
，
，
．
在
中，由余弦定理，
…6分
由正弦定理
，
，即
，
．
在
中，由已知
，由余弦定理，
． …12分
乙船的速度的大小为海里/小时．
答：乙船每小时航行海里．
………………14分
21．解：（Ⅰ）由题意得:
………………3分
由得 :
或
（舍去），
所以
或
，即的实不动点为或
；
……………6分
（II）由条件得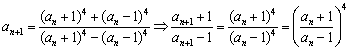
…………8分
从而有
，
…………………10分
由此及
知：数列
是首项为
，公比为
的等比数列，
故有
（）. ………………14分