向量及其运算习题课
一. 教学内容：
向量及其运算习题课
二. 重点与难点：
1. 向量的概念：向量是既有大小，又有方向的量。向量的大小（长度）叫做向量的模，模是非负数，可以比较大小，但由于方向不能比较大小，所以，向量不可以比较大小，这是数量与向量的最大差异。
2. 向量的表示方法：
（1）几何表示法。向量可以用有向线段表示，如：A→B
3. 零向量与单位向量：
零向量：长度为零的向量叫做零向量，记作0。
单位向量：长度等于1个单位长度的向量叫做单位向量。
4. 平行向量、相等向量、共线向量。
平行向量（共线向量）：方向相同或相反的非零向量叫做平行向量。规定0与任一向量平行，平行向量也叫做共线向量。
相等向量：长度相等且方向相同的向量叫做相等向量。任意两个相等的非零向量都可以用同一条有向线段表示。
5. 向量的加法：
法。
注意：（1）两个向量的和仍为向量。
（2）对于零向量与任一向量a有a+0=0+a=a。
6. 向量的加法法则
（1）三角形法则：（首尾连接）
（2）平行四边形法则：（共起点）
7. 向量的加法运算律。
（1）交换律：a+b=b+a
（2）结合律：a+(b+c)=(a+b)+c
8. 相反向量：与a长度相等，方向相反的向量叫做a的相反向量，记作-a。
零向量的相反向量为零向量。
相反向量性质：
9. 向量的减法：向量a加上向量b的相反向量叫做a与b的差。记
求两个向量差的运算叫做向量的减法。
10. 实数与向量的积：
实数λ与向量a的积是一个向量，记作λa，它的长度与方向规定如下：
11. 实数与向量的积的运算律：
12. 一个向量与非零向量共线的充要条件：
向量b与非零向量a共线的充要条件是有且只有一个实数λ，使得b=λa。
13. 平面向量的基本定理：如果e1、e2是平面内的两个不共线向量，那么对于这一平面
把不共线的向量e1、e2叫做表示这一平面内所有向量的一组基底。
14. 向量坐标的概念。
若i，j分别是与平面直角坐标系内x轴，y轴方向相同的单位向量，且a=xi+yj，则x叫a在x轴上的坐标，y叫a在y轴上的坐标（不要说成横坐标，纵坐标）。记作a=(x,y)。
15. 相等向量坐标的关系。
与向量a=（x，y）相等的所有向量的坐标均为（x，y）。
16. 向量坐标公式
17. 向量的和、差及实数与向量的积的坐标公式：
18. 向量共线定理：
向量a与非零向量b共线的充要条件是：有且只有一个实数λ，使a=λb。
19. 平行向量的坐标关系：
20. 点分有向线段所成的比的概念。
21. 分点坐标公式。
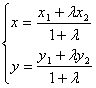
此公式叫定比分点坐标公式。在此公式中，（x1，y1），(x2，y2)，（x，y）分别表示起点，终点，分点的坐标。
22. 中点坐标公式
此即为线段的中点坐标公式。
23. 三角形重心坐标公式。
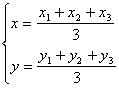
24. 向量的夹角的概念
叫做a，b的夹角。
注意：（1）两个非零向量的夹角的范围为：
25. a与b的数量积的概念
已知两个非零向量a和b，它们的夹角为θ，则数量abcosθ叫做a与b的数量积（内积），记作a·b。
注意：（1）a与b的数量积的结果是一个实数（可为正数、负数或零）。
26. b在a方向上的投影。
注意：（1）b在a方向上的投影不是向量而是一个实数，它的符号取决于θ角的范围。
（2）a在b方向上的投影acosθ。
27. a·b的几何意义
数量积a·b等于a的长度a与b在a方向上的投影bcosθ的乘积，也等于b的长度b与a在b方向上的投影acosθ的乘积。
28. 数量积的重要性质
设a，b均为非零向量，e是与b方向相同的单位向量，θ是a与e的夹角（则a与b的夹角也为θ），由数量积的定义可得如下五条重要性质：
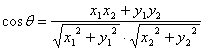
33. 在平移向量a及平移前后函数图象的解析式y=f(x)，y=g(x)三者之中，知道了两个能求出第三个。
［例题选讲］
例1. 设a、b是非零向量，且a与b不平行，求证a+b与a-b不平行。
分析：如果结论不成立，即(a+b)//(a-b)，将会得到什么样的结果呢？因为两个向量共线，必定存在一个实数λ，使一个向量的λ倍恰好等于另一个向量。由此得到的关于a、b的等式就能推出与题设矛盾。
解：
小结：命题由否定形式出现，通常可考虑用反证法来证明。因为本题难度不大，所以也可直接利用向量平行的充要条件验证。如，
例2. 
分析：（1）注意c2=c2，根据向量数量积的定义及运算律先求出c2；
解：
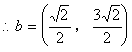
小结：第（2）题把题中的向量a的起点设为原点，在图中旋转容易理解，但实际上与起点的位置无关。解题的思路能推广到一般情况。另外，结合图形可知n>1，从而在二元二次方程组的解中选取适合题意的解。
例3. 
分析：
解：
小结：直接用代数的方法求本题中的函数最值很困难，一般情况下转化为几何模型求解。这里借助向量计算，本质上还是几何模型，但运算简捷了。
例4. 如图所示，P、Q是△ABC的边BC上两点，且BP=QC。
求证：
证明：
小结：
例5. 
解：
小结：
例6. 
解法一：
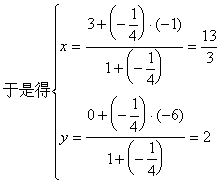
解法二：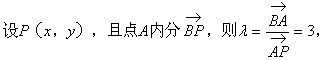
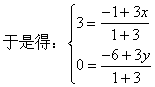
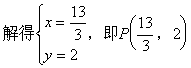
小结：在采用定比分点公式解题时，起点、终点、分点及相应的比值λ都是相对的，它们的位置关系可以根据问题的特点作适当调整。
例7. 
解法一：
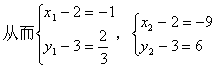
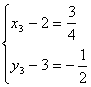
解法二：
由定比分点公式，可得：
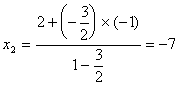
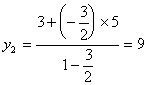
小结：本题是向量坐标表示的典型题，方法一主要是运用若向量相等，则其坐标相等这一原则来解，思路清晰，易于理解，方法二主要运用定比分点公式求点的坐标，此题关
形式，从而分别求出λ。
例8. 
解：
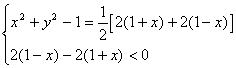
小结：本例为2002年高考题（21）题第（1）小题，主要考查向量的数量积的坐标表示及等差数列基础知识等。
例9. 
解法一：
解法二：
小结：从本例可以看出，如果把函数图像的解析式从一种形式变为另一种形式有两种方法，这两种方法实质相同，都应对此深刻理解。
【模拟试题】
一. 选择题
1. 下列说法中正确的是（ ）
A. 两个长度相等的向量一定相等，
B. 相等的向量起点必相同
C. 
共线，则A、B、C、D四点必在同一直线上
D. 相等的向量一定是平行向量
2. 向量
A. 充分不必要条件
B. 必要非充分条件
C. 充要条件
D. 非充分也非必要条件
3. 
为非零向量，且
，则（ ）
A. 
方向相同
B. 
C. 
D. 以上都不对
4. 化简
的结果是（ ）
A. 
B. 
C. 
D. 
5. 若
，则向量
=（ ）
A. 
B. 
C. 
D. 
6. 在四边形ABCD中，
，
，其中
、
不共线，则四边形ABCD为（ ）
A. 平行四边形 B. 矩形 C. 梯形 D. 菱形
7. 若
三点共线，则（ ）
A. 
B.
C. 
D.
8. 与向量
平行的向量是（ ）
A. 
B.
C. 
D.
9. 已知两点
分有向线段
所成的比
A. 
B.
C. 
D.
10. 已知点P分
A. 
B. 
C. 
D. 
11. 已知
的三个值分别是（ ）
A. 
B. 
C. 
D. 以上答案都不对
12. 若把一个函数的图象按
平移后得到函数
的图象，则原函数的解析式为（ ）
A. 
B. 
C. 
D. 
二. 填空题
13. 若
，则
的夹角为________________。
14. 已知
，则k=___________
15. 已知
_________，
______
16. 已知
___________
三. 解答题
17. 设
，
，若A、B、D三点共线，试求k的值。
18. 已知向量
，且
，求x的值。
19. 已知
，求的夹角。
20. 平面内有向量
，点C为直线
上的一动点，（1）当
取最小值时，求
的坐标。（2）当点C满足（1）时，求
的值。
【试题答案】
一. 选择题
1. D 2. B 3. A 4. B 5. B
6. C 7. B 8. A 9. A 10. C
11. C 12. D
二. 填空题
13. 
14.
15. 
16.
三. 解答题
17. 设
是两个不共线向量，已知
，
，若A、B、D三点共线，试求k的值。
解：
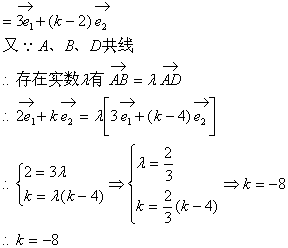
18. 已知向量
，且，求x的值。
解：
19. 已知，求的夹角。
解：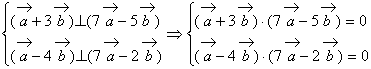
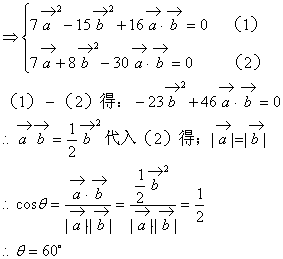
20. 平面内有向量，点C为直线上的一动点，（1）当取最小值时，求的坐标。（2）当点C满足（1）时，求的值。
解：（1）设
（2）
