08届高考理科数学第二次调研考试试题
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中.只有一项是符合题目要求的.
1、设函数![]() 的定义域为集合M,集合N=
的定义域为集合M,集合N=![]() ,则
,则![]() ( ).
( ).
 A.
A.![]() B.N C.
B.N C.![]() D.M
D.M
2、已知椭圆的长轴长是短轴长的![]() 倍,则椭圆的离心率等于( ).
倍,则椭圆的离心率等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
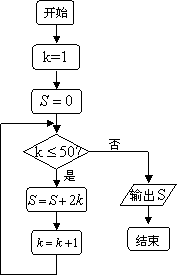
3、如果执行的程序框图(右图所示),那么输出的![]() ( ).
( ).
A.2450 B.2500 C.2550 D.2652
4、若曲线![]() 的一条切线
的一条切线![]() 与直线
与直线![]()
垂直,则切线![]() 的方程为( ).
的方程为( ).
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、方程![]() 有实根的概率为( ).
有实根的概率为( ).
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6、已知![]() 是平面,
是平面,![]() 是直线,则下列命题中不正确的是( ).
是直线,则下列命题中不正确的是( ).
A、若![]() ∥
∥![]() ,则
,则![]() B、若
B、若![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
 C、若
C、若![]()
![]() ,则
,则![]() ∥
∥![]() D、若
D、若![]()
![]() ,则
,则![]()
![]()
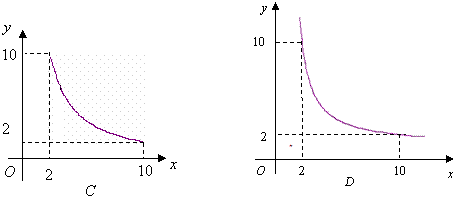
7、一张正方形的纸片,剪去两个一样的小矩形得到一个“![]() ”图案,
”图案,
如图所示,设小矩形的长、宽分别为![]() 、
、![]() ,剪去部分的面积为
,剪去部分的面积为![]() ,
,
若![]() ,记
,记![]() ,则
,则![]() 的图象是( ).
的图象是( ).
 |
8、将函数![]() 的图象先向左平移
的图象先向左平移![]() ,然后将所得图象上所有点的横坐标变为原来的
,然后将所得图象上所有点的横坐标变为原来的![]() 倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
第Ⅱ卷(非选择题,共110分)
二、填空题:本大题共7小题,其中13~15题是选做题,考生只能选做两题,三题全答的,只计算前两题得分.每小题5分,满分30分.
9、已知向量![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() 的值等于
.
的值等于
.
10、已知![]() ,则
,则![]() =
.
=
.
11、![]() 是虚数单位,则
是虚数单位,则![]() .
.
12、函数![]() 由下表定义:
由下表定义:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
13、(坐标系与参数方程选做题)曲线![]() :
:![]() 上的点到曲线
上的点到曲线![]() :
: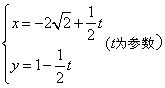 上的点的最短距离为
.
上的点的最短距离为
.
14、(不等式选讲选做题)已知实数![]() 满足
满足![]() ,则
,则![]() 的最大值为 .
的最大值为 .
15、(几何证明选讲选做题)如图,平行四边形![]() 中,
中,
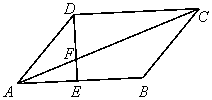
![]() ,若
,若![]() 的面积等于1cm
的面积等于1cm![]() ,
,
则![]() 的面积等于
cm
的面积等于
cm![]() .
.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16、(本小题满分12分)设正项等比数列![]() 的前
的前![]() 项和为
项和为![]() , 已知
, 已知![]() ,
,![]() .
.
(Ⅰ)求首项![]() 和公比
和公比![]() 的值;
的值;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
17、(本小题满分12分)设函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当![]() 时,
时,![]() 的最大值为2,求
的最大值为2,求![]() 的值,并求出
的值,并求出![]() 的对称轴方程.
的对称轴方程.
18、(本小题满分14分)一个口袋中装有大小相同的2个白球和4个黑球.
(Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
(方差:![]() )
)
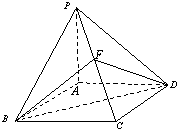 19、(本小题满分14分)如图,已知四棱锥
19、(本小题满分14分)如图,已知四棱锥![]() 的
的
底面![]() 是菱形;
是菱形;![]() 平面
平面![]() ,
,![]() ,
,
点![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正切值.
的正切值.
 20、(本小题满分14分)给定圆P:
20、(本小题满分14分)给定圆P:![]() 及抛物
及抛物
线S:![]() ,过圆心
,过圆心![]() 作直线
作直线![]() ,此直线与上述两曲线
,此直线与上述两曲线
的四个交点,自上而下顺次记为![]() ,如果线
,如果线
段![]() 的长按此顺序构成一个等差数列,求直
的长按此顺序构成一个等差数列,求直
线![]() 的方程.
的方程.
21、(本小题满分14分)设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]()
![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() ”.
”.
(Ⅰ)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(Ⅱ)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意[m,n]
的定义域为D,则对于任意[m,n]![]() D,都存在
D,都存在![]()
![]() [m,n],使得等式
[m,n],使得等式![]() 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(Ⅲ)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() .
.
参考答案
一、选择题:
| 题号 |
|
|
|
|
|
|
|
|
| 答案 |
|
|
|
|
|
|
|
|
1、解析:![]() ,N=
,N=![]() ,
,
即![]() .答案:
.答案:![]() .
.
2、解析:由题意得![]() ,又
,又![]() .
.
答案:![]() .
.
3、解析:程序的运行结果是![]() .答案:
.答案:![]() .
.
4、解析:与直线![]() 垂直的切线
垂直的切线![]() 的斜率必为4,而
的斜率必为4,而![]() ,所以,切点为
,所以,切点为![]() .切线为
.切线为![]() ,即
,即![]() ,答案:
,答案:![]() .
.
5、解析:由一元二次方程有实根的条件![]() ,而
,而![]() ,由几何概率得有实根的概率为
,由几何概率得有实根的概率为![]() .答案:
.答案:![]() .
.
6、解析:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,所以![]() 正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以
正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以![]() 正确;
正确;
如果一个平面经过了另一个平面的一条垂线,则这两个平面平行,所以![]() 也正确;
也正确;
只有![]() 选项错误.答案:
选项错误.答案:![]() .
.
7、解析:由题意,得![]() ,答案:
,答案:![]() .
.
8、解析:![]() 的图象先向左平移
的图象先向左平移![]() ,横坐标变为原来的
,横坐标变为原来的![]() 倍
倍![]() .答案:
.答案:![]() .
.
二、填空题:
| 题号 |
|
|
|
|
|
|
|
| 答案 |
|
|
|
|
|
|
|
9、解析:若![]() ,则
,则![]() ,解得
,解得![]() .
.
10、解析:由题意![]() .
.
11、解析:![]()
![]()
12、解析:令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
…,所以![]() .
.
13、解析:![]() :
:![]() ;则圆心坐标为
;则圆心坐标为![]() .
.
![]() :
: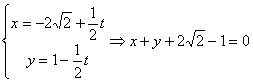 由点到直线的距离公式得圆心到直线的距离为
由点到直线的距离公式得圆心到直线的距离为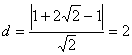 ,所以要求的最短距离为
,所以要求的最短距离为![]() .
.
14、解析:由柯西不等式![]() ,答案:
,答案:![]() .
.
15、解析:显然![]() 与
与![]() 为相似三角形,又
为相似三角形,又![]() ,所以
,所以![]() 的面积等于9cm
的面积等于9cm![]() .
.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16、解: (Ⅰ)![]()
![]() , ……………………… 2分
, ……………………… 2分
∴![]() ,………………………………………………… 4分
,………………………………………………… 4分
解得![]() .………………………………………………………………… 6分
.………………………………………………………………… 6分
(Ⅱ)由![]() ,得:
,得:![]() , ……………………… 8分
, ……………………… 8分
∴![]() ………………………………… 10分
………………………………… 10分
∴![]() .…………………………………………………………… 12分
.…………………………………………………………… 12分
17、解:(1)![]() … 2分
… 2分
则![]() 的最小正周期
的最小正周期![]() , …………………………………4分
, …………………………………4分
且当![]() 时
时![]() 单调递增.
单调递增.
即![]() 为
为![]() 的单调递增区间(写成开区间不扣分).………6分
的单调递增区间(写成开区间不扣分).………6分
(2)当![]() 时
时![]() ,当
,当![]() ,即
,即![]() 时
时![]() .
.
所以![]() . …………………………9分
. …………………………9分
![]() 为
为![]() 的对称轴. …………………12分
的对称轴. …………………12分
18、解:
(Ⅰ)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,
记“有放回摸球两次,两球恰好颜色不同”为事件![]() ,………………………2分
,………………………2分
∵“两球恰好颜色不同”共![]() 种可能,…………………………5分
种可能,…………………………5分
∴![]() . ……………………………………………………7分
. ……………………………………………………7分
解法二:“有放回摸取”可看作独立重复实验, …………………………2分
∵每次摸出一球得白球的概率为![]() .………………………………5分
.………………………………5分
∴“有放回摸两次,颜色不同”的概率为![]() . ……………………………7分
. ……………………………7分
(Ⅱ)设摸得白球的个数为![]() ,依题意得:
,依题意得:
![]() ,
,![]() ,
,![]() .…………10分
.…………10分
∴![]() ,……………………………………12分
,……………………………………12分
![]() .……………………14分
.……………………14分
19、(Ⅰ)证明: 连结![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() .………………………1分
.………………………1分
![]()
![]() 是菱形, ∴
是菱形, ∴![]() 是
是![]() 的中点. ………………………………………2分
的中点. ………………………………………2分
![]() 点
点![]() 为
为![]() 的中点, ∴
的中点, ∴![]() . …………………………………3分
. …………………………………3分
![]() 平面
平面![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() . ……………… 6分
. ……………… 6分
 (Ⅱ)解法一:
(Ⅱ)解法一:
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴ ![]() .
.
![]() ,∴
,∴![]() . …………………………… 7分
. …………………………… 7分
![]()
![]() 是菱形, ∴
是菱形, ∴![]() .
.
![]() ,
,
∴![]() 平面
平面![]() . …………………………………………………………8分
. …………………………………………………………8分
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,则
,则![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角. ………………………………… 10分
的平面角. ………………………………… 10分
![]()
![]() ,∴
,∴![]() ,
,![]() .
.
在Rt△![]() 中,
中,![]() =
=![]()
![]() ,…………………………… 12分
,…………………………… 12分
∴ .…………………………… 13分
.…………………………… 13分
∴二面角![]() 的正切值是
的正切值是![]() . ………………………… 14分
. ………………………… 14分
解法二:如图,以点![]() 为坐标原点,线段
为坐标原点,线段![]() 的垂直平分线所在直线为
的垂直平分线所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,令
轴,建立空间直角坐标系,令![]() ,……………2分
,……………2分
则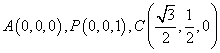 ,
,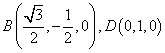 ,
,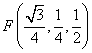 .
.
 ∴
∴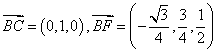 . ……………4分
. ……………4分
设平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,
,
由![]()
![]()
![]()
![]() ,得
,得 ,
,
令![]() ,则
,则![]() ,∴
,∴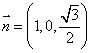 . …………………7分
. …………………7分
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() . ………………………………… 8分
. ………………………………… 8分
![]() ,∴
,∴![]() .
.
![]()
![]() 是菱形,∴
是菱形,∴![]() .
.
![]() ,∴
,∴![]() 平面
平面![]() .…………………………… 9分
.…………………………… 9分
∴![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]()
![]() .………………… 10分
.………………… 10分
∴ ,
,
∴ , …………………… 12分
, …………………… 12分
∴ .…………………………………… 13分
.…………………………………… 13分
∴二面角![]() 的正切值是
的正切值是![]() . ……………………… 14分
. ……………………… 14分
20、解:圆![]() 的方程为
的方程为![]() ,则其直径长
,则其直径长![]() ,圆心为
,圆心为![]() ,设
,设![]() 的方程为
的方程为![]() ,即
,即![]() ,代入抛物线方程得:
,代入抛物线方程得:![]() ,设
,设![]() ,
,
 有
有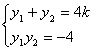 , ………………………………2分
, ………………………………2分
则![]() . ……………………4分
. ……………………4分
故![]() …6分
…6分
![]() , ………… 7分
, ………… 7分
因此![]() . ………………………………… 8分
. ………………………………… 8分
据等差,![]() , …………… 10分
, …………… 10分
所以![]() ,即
,即![]() ,
,![]() ,…………… 12分
,…………… 12分
即:![]() 方程为
方程为![]() 或
或![]() . …………………14分
. …………………14分
21、解:
(1)因为![]() , …………………………2分
, …………………………2分
所以![]() ,满足条件
,满足条件![]() . …………………3分
. …………………3分
又因为当![]() 时,
时,![]() ,所以方程
,所以方程![]() 有实数根
有实数根![]() .
.
所以函数![]() 是集合M中的元素. …………………………4分
是集合M中的元素. …………………………4分
(2)假设方程![]() 存在两个实数根
存在两个实数根![]() ),
),
则![]() ,……………………………………5分
,……………………………………5分
不妨设![]() ,根据题意存在数
,根据题意存在数![]()
使得等式![]() 成立, ………………………7分
成立, ………………………7分
因为![]() ,所以
,所以![]() ,与已知
,与已知![]() 矛盾,
矛盾,
所以方程![]() 只有一个实数根;………………………10分
只有一个实数根;………………………10分
(3)不妨设![]() ,因为
,因为![]() 所以
所以![]() 为增函数,所以
为增函数,所以![]() ,
,
又因为![]() ,所以函数
,所以函数![]() 为减函数, ……………………11分
为减函数, ……………………11分
所以![]() , ………………………………12分
, ………………………………12分
所以![]() ,即
,即![]() , …………13分
, …………13分
所以![]() . …14分
. …14分